voltamperometrico

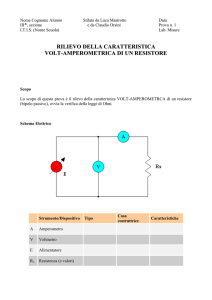
UNIVERSITÀ DEGLI STUDI DI CATANIA
Facoltà di Ingegneria
Dipartimento Elettrico, Elettronico e Sistemistico
Corso di Misure Elettriche
Anno Accademico 2000-2001
Prof. Nicola Pitrone
Relazione su
IL METODO VOLTAMPEROMETRICO
Gruppo di lavoro:
Filippo Chimento
Francesco Conticello
Pasquale Di Maggio
Federico Giordano
Enrico Perez
Guido Vagliasindi
Dicembre 2000
Il metodo voltamperometrico
© ing.elettrics_2000/2001
Quando si vuole effettuare una qualunque misura occorre innanzi tutto stabilire la
precisione con cui si vuole compiere tali misure. A seconda, poi, della precisione,
occorre scegliere il metodo e le apparecchiature. Occorre dunque eseguire le
misurazioni e fare l’analisi degli errori.
Le misure si distinguono in dirette ed indirette. Le prime si ottengono mediante un
confronto diretto tra le grandezze da misurare e il campione omogeneo scelto. Le
seconde si realizzano attraverso delle relazioni analitiche che collegano le grandezze
in questione ed altro ottenibili direttamente.
Il metodo voltamperometrico è tra tutti il meno preciso per la misura indiretta di una
resistenza. Usando, però, degli strumenti precisi per la misura di V ed I è possibile
ottenere dei buoni risultati.
Gli strumenti usati per le misurazioni si dividono in:
1. Strumenti elettromeccanici
2. Strumenti elettronici: a) analogici
b) numerici
Gli strumenti elettromeccanici sono costituiti da un indice che ruota su di una scala
graduata per effetto di una coppia (azione esterna) fornita dalla grandezza che viene
misurata.
Gli strumenti elettronici analogici presentano al loro interno delle parti
elettromeccaniche, ma l’azione esterna che serve a far muovere l’indice è fornita
dall’apparecchio stesso, anzi, per meglio dire, deriva dalle grandezze esterne dalle
quali si preleva una piccola parte fornita ad un amplificatore. All’uscita di questo poi
è prelevata la coppia motrice.
Mentre gli strumenti analogici modificano lievemente la misura quelli
elettromeccanici la modificano notevolmente in quanto assorbono notevoli potenze
dal circuito. Inoltre gli strumenti analogici hanno un migliore comportamento al
variare della frequenza rispetto a quelli elettromeccanici.
Al contrario la precisione di quelli elettronici analogici è più bassa di quelli
elettromeccanici in quanto oltre alla parte elettromeccanica presente in entrambi i tipi
si ha in essi un errore aggiuntivo dovuto alla parte elettronica.
Gli strumenti numerici, infine, sono diversi dai primi due visti sia per il principio di
funzionamento che per la precisione.
Il metodo voltamperometrico
© ing.elettrics_2000/2001
Il metodo voltamperometrico
Il metodo voltamperometrico è un metodo indiretto di misura in quanto si basa su
una relazione analitica dipendente da grandezze diverse rispetto a quella da misurare:
ad esempio si può ricavare la misura di una resistenza valutando la corrente che
l'attraversa e la tensione ai sui capi R = V/I (legge di Ohm).
Bisogna però sottolineare che le relazioni analitiche da noi utilizzate nella realtà non
hanno validità assoluta ma risultano influenzate da variabili esterne quali
temperatura, frequenza.
L'applicazione del metodo richiede:
• un'opportuna modellizzazione dell'elemento oggetto della misura e della
componentistica costituente il circuito che dovrà effettuarla;
• la scelta degli strumenti in base ai loro principi di funzionamento ed alle loro
caratteristiche;
• l'individuazione delle grandezze di influenza;
• la valutazione di eventuali errori sistematici e accidentali;
• l'inserzione degli strumenti di misura.
MISURE DI RESISTENZA IN CORRENTE CONTINUA
Innanzitutto bisogna osservare che il resistore è un elemento passivo e quindi
misurabile solo se sottoposto ad una sollecitazione attiva, tensione o corrente. Inoltre
prima di effettuare la scelta del metodo e quindi la misura è necessario conoscere
l’ordine di grandezza della resistenza da misurare e la precisione richiesta.
Il circuito atto alla misura è costituito da un generatore di tensione costante in serie
ad un resistore variabile e al resistore da misurare (vedi fig.1). E’ necessario
conoscere la massima corrente che può sopportare R, per evitare che il resistore
variabile sia così piccolo da far passare una corrente più grande di quella sopportabile
da R, cosa che ne provocherebbe la rottura.
R'
R
E
Fig. 1
Vanno poi opportunamente inseriti gli strumenti di misura ovvero un amperometro,
collegato in serie tra i due resistori, e un voltmetro a monte (vedi Fig. 3) o a valle
3
Il metodo voltamperometrico
© ing.elettrics_2000/2001
(vedi Fig. 4) dell'amperometro. Nell’assemblamento del circuito di prova, è buona
norma seguire esattamente lo schema elettrico, connettendo prima i componenti della
maglia esterna, e solo dopo gli elementi in parallelo. Si può allora collegare il
voltmetro in qualunque momento senza modificare la topologia del circuito; inoltre si
deve comunque aspettare che tutti i transitori si siano estinti: ad esempio, nella
misura della resistenza dell’avvolgimento di una macchina elettrica, in transitorio si
verificano sovratensioni che possono distruggere il voltmetro, e questo è un
problema. Invece, l’inserimento o l’eliminazione dell’amperometro comporterebbe
l’apertura della maglia esterna, se prima esso non fosse cortocircuitato.
A
A
Fig. 2
L'inserimento del voltmetro comporta un errore rispettivamente sulla tensione e
sulla corrente afferente al resistore.
Studiamo nel dettaglio le due possibili configurazioni.
Nella configurazione a monte
R'
IM
A
E
R
V
Fig. 3
la corrente IM misurata dall'amperometro è quella che effettivamente attraversa il
resistore IR. La tensione VM misurata dal voltmetro risulta essere la somma della
tensione VR ai capi del resistore e della tensione VA ai capi dell'amperometro:
I R = I M

VM = VR + VA = VR + R A I M
dove RA è la resistenza interna dell'amperometro.
4
Il metodo voltamperometrico
© ing.elettrics_2000/2001
Nella configurazione a valle
R'
IR
IM
A
IV
V
E
R
Fig. 4
la corrente IM misurata dall'amperometro è la somma della corrente IR e della corrente
IV che attraversa la resistenza interna RV del voltmetro. La tensione VM misurata dal
voltmetro è l'effettiva tensione VR ai capi del resistore oggetto di misura.
VM

 I M = I R + IV = I R +
RV

V = V
R
 M
In entrambi i casi si commette un errore sistematico, cioè un errore che dipende
dall'inserzione del voltmetro e del quale si conosce il segno. Rispettivamente gli
errori sono rappresentati dai due termini
RA ⋅ I M
nel caso di voltmetro a monte;
VM
RV
nel caso di voltmetro a valle;
Quindi si deve tenere conto di essi nella scelta dell'inserzione. Ciò si può fare
valutando i rapporti
RA
che tiene conto dell'errore commesso quando il voltmetro è a monte. Nel
R
caso ideale, cioè per R A → 0 , l'errore tende anch'esso ad annullarsi.
R
−
che tiene conto dell'errore commesso quando il voltmetro è a valle.
RV
−
Analogamente, per R V → ∞ , l'errore si annulla.
Per valutare tali valori e per operare una scelta accurata degli strumenti è necessario
farsi comunque prima un idea del valore di R.
L'errore sistematico nella misura può essere eliminato in virtù del fatto che se ne
conosce il segno, e questo è un vantaggio. La scelta di una dei due metodi va allora
fatta in base all’inserzione che fornisce un errore relativo sistematico più piccolo.
5
Il metodo voltamperometrico
© ing.elettrics_2000/2001
Un altro tipo di errore che si ha quando si effettua una misura è l'errore
accidentale, del quale non si conosce il segno. L'errore accidentale è causato
dall'attrito che si ha tra l'equipaggio mobile dello strumento e i suoi supporti.
L’errore accidentale fa si che non si conosca il valore dell’errore sistematico.
Quando si effettua una misura, la lancetta dello strumento andrà ad indicare un punto
sulla scala, compreso fra due divisioni della stessa, individuando così non un
determinato valore (comunque affetto da errore accidentale), ma un intervallo di
valori, che sono tutti accettabili ai fini della misura (fascia di incertezza).
Gli strumenti magnetoelettrici sono costituiti da una parte mobile (rotante) e da un
asse fisso. Tra i perni esiste una forza d’attrito opposta al verso di rotazione e quindi
la posizione finale del perno dipende dal verso dell’ultima oscillazione: se il verso
dell’ultima oscillazione è da sinistra verso destra il valore effettivo è più spostato a
destra perché la forza d’attrito ha trattenuto l’indice in quella posizione, e viceversa.
N
N+1
2
T-1
1
T
0
Così, se ad esempio un amperometro misura un valore di corrente compreso fra la
divisione n-esima e quella n+1-esima, il risultato della misura è che la corrente IM è
pari a:
I M = [(n + 0.5 ) ± (0.5)]⋅ k s Ampere
in cui ks è la costante dello strumento, cioè il valore numerico di ogni divisione
della scala dello strumento:
KS =
P
nT
cioè il rapporto tra portata massima dello strumento e il numero totale di divisioni
della scala.
La quantità 0.5KS è l’errore assoluto, cioè l’errore totale massimo che si commette
nell’effettuare la misura.
Un altro parametro fondamentale indicativo dell’errore accidentale di una misura, è
l’errore relativo, dato dal rapporto fra errore massimo e il valore della misura:
δ=
ε MAX
;
X MIS
6
Il metodo voltamperometrico
© ing.elettrics_2000/2001
l’errore relativo, per sua definizione, è minimo quando la lettura è effettuata al fondo
della scala dello strumento. In queste condizioni, esso assume il valore dell’indice di
classe n dello strumento: n è rappresentativo della sua precisione ed è determinato
dagli attriti interni:
ε
n = 100 MAX [%]
P
quindi, poiché n è un dato di targa, è possibile determinare l’errore massimo
commesso:
nP
ε MAX =
100
Ne consegue che l’errore relativo in un punto qualunque diverso dal fondoscala è più
alto dell’indice di classe: questo comporta che a fondoscala si ha il più piccolo errore
relativo ed è quindi più opportuno effettuare le misure quanto più possibile in questa
zona.
PROPAGAZIONE DEGLI ERRORI NELLE MISURE INDIRETTE.
Una misura indiretta, si è detto, consiste nell’ottenere il valore della grandezza da
misurare da un legame analitico del tipo
x = f ( a1 , a 2 ,..., a n )
in cui a1, a2,…,an sono le grandezze che si misurano direttamente e sono affette da
errore.
Allora l’errore su ognuna di questa grandezze influenzerà l’errore su x. Occorre
allora calcolare l’errore totale su x. Esso sarà dato dalla media pesata degli errori
commessi su ciascuna misura diretta:
∂f
∂f
∂f
εx =
ε a1 +
ε a2 + ... +
εa
∂a1
∂a 2
∂a n n
Da qui, calcolare l’errore relativo sarà facile, infatti:
εx
δx =
f (a1 , a 2 ,..., a n )
Nel caso particolare della misura di un resistore R, le grandezze misurate
direttamente sono V e I, mentre R=V/I. Allora si ha:
εR =
∂R
∂R
εV +
εI
∂V
∂I
dove abbiamo usato il valore assoluto perché essendo dei valori casuli dobbiamo
considerare il caso peggiore.
Quindi:
1
V
ε R = εV + − 2 ε I
I
I
7
Il metodo voltamperometrico
© ing.elettrics_2000/2001
V
1
ε R = εV + 2 ε I
I
I
L’errore relativo allora sarà pari a:
ε
1
V
δR = R =
εV +
εI
R RI
RI 2
1 εV
=
= δV
RI V
ε
V
εI
= i =δI
2
I
RI
εV
Cioè, l’errore relativo su R è dato dalla somma degli errori relativi su V e I:
δ R =δv + δi
Se, allora, la misura fatta si ottiene per somma o differenza di misure dirette, la
misura della grandezza più piccola può essere fatta anche con un errore relativo molto
grande in quanto l’errore assoluto, che poi è quello che si deve sommare, risulta
comunque essere piccolo.
MISURA DI PICCOLE RESISTENZE.
Le resistenze di piccolo valore e i conduttori che realizzano i vari collegamenti
hanno sezione elevata per permettere il passaggio di grandi correnti; collegando il
voltmetro ai terminali del resistore da misurare si può avere una lettura falsata, infatti
la superficie esterna di contatto, in genere, non è equipotenziale, e presenta una certa
resistenza di contatto.
Al fine di realizzare misure più precise, si impiegano resistenze a 4 morsetti, 2
amperometrici , atti a realizzare il collegamento fra resistore e resto del circuito e 2
voltmetrici a cui si collega il voltmetro (Fig. 5).
V
R
Fig. 5
E’ ovvio che si ha una resistenza di contatto anche ai morsetti voltmetrici, ma questi
sono di dimensioni molto ridotte e percorsi da correnti piccolissime, data
l’elevatissima resistenza del voltmetro rispetto a quella da misurare, quindi l’errore
che si commette è trascurabile.
8
Il metodo voltamperometrico
© ing.elettrics_2000/2001
MISURA DI GRANDI RESISTENZE.
Quando si devono misurare resistenze nell’ordine del MΩ, quindi confrontabili con
la resistenza dell’aria (in genere molto più grande di quella delle resistenze più
comuni), una parte della corrente si disperde nell’aria circostante il resistore (Fig. 6).
Per ovviare a questo problema, si utilizza una schermatura opportuna.
A
Fig. 6
9
Il metodo voltamperometrico
© ing.elettrics_2000/2001
LABORATORIO SUL METODO VOLTAMPEROMETRICO
Misura di un resistore in corrente continua
La misura di un resistore in corrente continua può essere effettuata tramite il metodo
voltamperometrico ovvero ricavando il valore della resistenza tramite una misura
indiretta di tensione e corrente. Le due grandezze possono essere ricavate tramite due
strumenti di misura, un amperometro ed un voltmetro, inseriti in maniera tale da
misurare contemporaneamente rispettivamente la corrente che attraversa il resistore e
la tensione ai suoi capi. Ci sono due possibilità di inserzione degli strumenti ovvero
quella con il voltmetro a valle dell’amperometro (Fig. 1) e quella con il voltmetro a
monte di esso(Fig. 2).
R'
A
V
E
R
Figura 1 : voltmetro a valle dell’amperometro
R'
A
E
R
V
Figura 2 : voltmetro a monte dell’amperometro
Entrambe le inserzioni comportano un errore sistematico che si presenta sempre
nella stessa direzione nella misura della resistenza. Tale errore è dovuto
all’autoconsumo degli strumenti e cioè alla non idealità di essi. Infatti nel primo caso
si ha un errore nella misura della corrente pari alla corrente assorbita dal voltmetro
che ha si un’elevata resistenza ma non infinita.
VM

 I M = I R + IV = I R +
RV

V = V
R
 M
10
Il metodo voltamperometrico
© ing.elettrics_2000/2001
Nel secondo caso invece l’errore inficia la misura di tensione dovuto alla caduta
sull’amperometro che ha si resistenza piccola ma non nulla.
I M = I R

VM = VR + V A = VR + RA I M
Tale errore si riflette nella misura della resistenza nel seguente modo:
ε % = 100⋅
IM − IR
I
V R
R
= 100⋅ V = 100⋅ M V = 100⋅
IR
IR
VM R
RV
nel caso di voltmetro a valle e
ε % = 100⋅
VM −VR
V
R ⋅I
R
= 100⋅ A = 100⋅ A M = 100⋅ A
VR
VR
R ⋅ IM
R
nel caso di voltmetro a monte.
Se tale errore non é notevolmente minore di quello che compete alla classe di
precisione degli strumenti impiegati occorre apportare la necessaria correzione,
determinando il valore della corrente mediante la relazione :
I R = I M − IV = I M −
VM
RV
e
VR = VM − V A = VM − R A ⋅ I M
Abbiamo utilizzato come resistenza campione da misurare un reostato da 10 Ω e
corrente massima 4,5 A. Per la costruzione del circuito di misura abbiamo prima
costruito la maglia esterna del circuito inserendo l’amperometro (A11) in serie al
resistore e collegando il tutto all’alimentazione. Abbiamo poi inserito il voltmetro
(V1) in parallelo al resistore o tra l’andata e il ritorno dell’alimentazione
rispettivamente nel caso di inserzione a valle o a monte. Abbiamo eseguito due
gruppi di misure per osservare le differenze tra i due tipi di misure.
1
Per le caratteristiche degli strumenti di misura vedere l’allegato “Strumenti di misura”
11
Il metodo voltamperometrico
© ing.elettrics_2000/2001
Ecco i risultati di essi:
Tabella 1a : misure con voltmetro a valle dell’amperometro
MISURA SUL VOLTMETRO
Misura
n°
1
2
3
Numero di
divisioni lette
41
60
72
K
0,5
0,5
0,5
Valore della
misura in V
20,5
30
36
MISURA SULL’AMPEROMETRO
Numero di
divisioni lette
40
59
70
K
0,05
0,05
0,05
Valore della
misura in A
2
2,9
3,5
RESISTENZA
Valore della
resistenza in Ohm
10,2
10,2
10,3
Tabella 1b : misure col voltmetro a monte dell’amperometro
MISURA SUL VOLTMETRO
Misura
n°
1
2
3
Numero di
divisioni lette
41
60
72
K
0,5
0,5
0,5
Valore della
misura in V
20,5
30
36
MISURA SULL’AMPEROMETRO
Numero di
divisioni lette
40
57
69
K
0,05
0,05
0,05
Valore della
misura in A
2
2,85
3,45
RESISTENZA
Valore della
resistenza in Ohm
10,2
10,5
10,4
Tabella 2a : errori nella misura con inserzione a valle
NV
VP
εR%
εA
nA
AP
εR%
εA
εsistR
εsistA
Rmisurata
εRtot%
εAtot
Rcorretta
0,2
65
0,63
0,13
0,5
5
1,25
0,03
0,62
0,06
10,2
1,88
0,19
10,3
0,2
0,2
65
65
0,43
0,36
0,13
0,13
0,5
0,5
5
5
0,85
0,71
0,03
0,03
0,62
0,62
0,06
0,06
10,2
10,3
1,28
1,08
0,13
0,11
10,2
10,3
Rmisurata
10,2
10,5
10,4
εRtot%
1,88
1,31
1,09
εAtot
0,19
0,14
0,11
Rcorretta
9,9
10,2
10,2
Tabella 2b : errori nella misura con inserzione a monte
nV
0,2
0,2
0,2
VP
65
65
65
εR%
0,63
0,43
0,36
εA
0,13
0,13
0,13
nA
0,5
0,5
0,5
AP
5
5
5
εR%
1,25
0,88
0,72
εA
0,03
0,03
0,03
εsistR
2,7
2,7
2,7
εsistA
0,27
0,27
0,27
Come si può vedere dalle tabelle 2a, 2b l’errore assoluto che si compie effettuando
la misura si suppone uguale in qualunque posizione della scala, di conseguenza esso
risulta essere meno influente quando la misura viene effettuata in prossimità del
fondoscala dello strumento come si può evincere dalla diminuzione dell’errore
relativo percentuale (εR%) man mano che il valore di tensione misurato sullo
strumento aumenta. Nella valutazione della resistenza non ci siamo potuti spingere
più vicini al fondo scala degli strumenti per non superare i 3,5 A sul reostato essendo
la corrente massima da esso sopportabile pari a 4,75 A.
12
Il metodo voltamperometrico
© ing.elettrics_2000/2001
Possiamo inoltre notare come la presenza dell’errore sistematico comporti nel caso
di inserzione a valle una valutazione in difetto della resistenza contro un valore in
eccesso nel caso di inserzione a monte.
Nelle tabelle 2a, 2b sono stati riportati oltre ai valori di resistenza corretti dell’errore
sistematico, anche l’errore nel calcolo di essa conseguenza degli errori insiti negli
strumenti di misura. Essendo, infatti, quella della resistenza col metodo
voltamperometrico una misura indiretta bisogna tenere conto degli errori commessi
nelle misure dirette e di come essi si propagano alla misura indiretta. In questo caso,
essendo la resistenza frutto di un rapporto tra due grandezze, abbiamo che l’errore
relativo che si commette nella misura della resistenza è la somma degli errori relativi
che si commettono nella misura della tensione e della corrente.
13
Il metodo voltamperometrico
© ing.elettrics_2000/2001
Misura della resistenza di una lampada ad incandescenza.
La resistenza di un metallo non è una grandezza costante ma variabile con la
temperatura con legge pressoché lineare per un ampio margine di temperatura. Scopo
di questa esperienza è la verifica dell’andamento variabile della resistenza in funzione
della temperature di una resistenza campione. La variazione di temperatura sulla
resistenza è effettuata sfruttando l’effetto Joule, ovvero la dissipazione di energia
elettrica in energia termica dovuta al passaggio di corrente attraverso la resistenza
secondo la legge:
V2
P = R⋅I =
R
2
Quindi possiamo provocare delle variazioni di temperatura semplicemente
modificando la corrente che attraversa la resistenza.
Come resistenza campione abbiamo scelto il filamento in tungsteno di una
lampadina ad incandescenza da 300 W a 220 V. Per effettuare la misura abbiamo
utilizzato il seguente circuito di misura in cui il voltmetro (V1) è inserito a valle
dell’amperometro (A2).
R'
A
W
Z
V
14
Il metodo voltamperometrico
© ing.elettrics_2000/2001
Tabella 3 : misure effettuate
MISURA SUL VOLTMETRO
Misura
n°
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
Numero di
divisioni lette
10
20
30
40
60
80
100
120
80
100
120
70
80
90
100
110
115
K
0,5
0,5
0,5
0,5
0,5
0,5
0,5
0,5
1,0
1,0
1,0
2,0
2,0
2,0
2,0
2,0
2,0
Valore della
misura in V
5
10
15
20
30
40
50
60
80
100
120
140
160
180
200
220
230
MISURA SULL'AMPEROMETRO
Numero di
divisioni lette
24
31
35,5
40
47,5
54,5
61
67,5
0,75
0,85
0,95
1,02
1,1
1,17
1,24
1,31
1,34
K
0,01
0,01
0,01
0,01
0,01
0,01
0,01
0,01
1,00
1,00
1,00
1,00
1,00
1,00
1,00
1,00
1,00
Valore della
misura in A
0,24
0,31
0,355
0,4
0,475
0,545
0,61
0,675
0,75
0,85
0,95
1,02
1,1
1,17
1,24
1,31
1,34
RESISTENZA
Valore della
resistenza in Ohm
20,8
32,2
42,2
50
63,1
73,4
81,9
88,9
106,6
117,6
126,3
137,2
145,4
153,8
161,3
167,9
171,6
Come si evince dalla tabella 3 il valore della resistenza del filamento aumenta al
crescere della corrente che in esso scorre o, che è lo stesso, della tensione a cui è
sottoposto. I valori sopra riportati sono inficiati dagli errori sistematici dovuti
all’inserzione degli strumenti e dagli errori accidentali.
Nella tabella 4 sono riportati i valori relativi ed assoluti di questi errori, i valori di
resistenza corretti dell’errore sistematico e la fascia di incertezza della misura ultima.
15
Il metodo voltamperometrico
© ing.elettrics_2000/2001
Tabella 4
NV
VP
εR%
εA
nA
AP
εR%
εA
εsistR
εsistA
Rmisurata
εRtot%
εAtot
Rcorretta
0,2
65
2,6
0,13
0,5
1,5
3,13
0,01
1,28
0,267
20,8
5,73
1,19
21,1
0,2
65
1,3
0,13
0,5
1,5
2,42
0,01
1,99
0,640
32,2
3,72
1,2
32,9
0,2
65
0,87
0,13
0,5
1,5
2,11
0,01
2,60
1,099
42,2
2,98
1,26
43,3
0,2
65
0,65
0,13
0,5
1,5
1,88
0,01
3,08
1,538
50,0
2,53
1,26
51,5
0,2
65
0,43
0,13
0,5
1,5
1,58
0,01
3,89
2,455
63,1
2,01
1,27
65,6
0,2
65
0,33
0,13
0,5
1,5
1,38
0,01
4,52
3,315
73,4
1,7
1,25
76,7
0,2
65
0,26
0,13
0,5
1,5
1,23
0,01
5,04
4,135
81,9
1,49
1,22
86,1
0,2
65
0,22
0,13
0,5
1,5
1,11
0,01
5,47
4,862
88,9
1,33
1,18
93,7
0,2
130
0,33
0,26
0,5
1,5
1
0,01
1,64
1,750
106,7
1,33
1,41
108,4
0,2
130
0,26
0,26
0,5
1,5
0,88
0,01
1,81
2,129
117,6
1,14
1,34
119,8
0,2
130
0,22
0,26
0,5
1,5
0,79
0,01
1,94
2,455
126,3
1,01
1,27
128,7
0,2
260
0,37
0,52
0,5
1,5
0,74
0,01
1,06
1,449
137,2
1,11
1,52
138,7
0,2
260
0,33
0,52
0,5
1,5
0,68
0,01
1,12
1,627
145,4
1,01
1,46
147,1
0,2
260
0,29
0,52
0,5
1,5
0,64
0,01
1,18
1,821
153,8
0,93
1,43
155,6
0,2
260
0,26
0,52
0,5
1,5
0,6
0,01
1,24
2,001
161,3
0,86
1,39
163,3
0,2
0,2
260
260
0,24
0,23
0,52
0,52
0,5
0,5
1,5
1,5
0,57
0,56
0,01
0,01
1,29
1,32
2,169
2,266
167,9
171,6
0,81
0,79
1,36
1,35
170,1
173,9
Nelle figure 3 e 4 sono riportati i grafici della resistenza in funzione della tensione
applicata e la legge di Ohm, ovvero l’andamento della corrente in funzione della
tensione.
Come si può osservare (fig.3), sebbene la resistenza vari linearmente con la
temperatura, essa non presenta un andamento lineare nel grafico perché la potenza
dissipata, e quindi la temperatura, non dipendono linearmente dalla tensione ma con
legge quadratica.
Nella figura 4 l’andamento non lineare della tensione rispetto alla corrente si
giustifica con il valore non costante della resistenza al variare delle stesse. Come si
può osservare, infatti, la pendenza della curva, che altro non è se non la resistenza,
aumenta all’aumentare della corrente
16
Il metodo voltamperometrico
© ing.elettrics_2000/2001
Figura 3 : andamento R-V
180
160
140
120
100
80
60
40
20
0
50
100
150
200
250
Volt
Figura 4 : andamento V-I
250
200
150
100
50
0
0.2
0.4
0.6
0.8
1
Ampere
1.2
1.4
1.6
17
Il metodo voltamperometrico
© ing.elettrics_2000/2001
STRUMENTI DI MISURA
Dati di targa
Voltmetro (V1):
•
•
•
•
Indice di classe n = 0.2
Portata = 65 V, 130 V, 260 V
Numero di divisioni = 130
Resistenza interna a 65 V = 1625 Ω
“
“
a 130 V = 6500 Ω
“
“
a 260 V = 13000 Ω
Millivoltmetro (V2):
•
•
•
•
Indice di classe n = 0.5
Portata = 75 mV
Numero di divisioni = 75
Autoconsumo = 7.5 mA
Amperometro (A1) :
•
•
•
•
Indice di classe n = 0.5
Portata = 5 A
Numero di divisioni = 100
Resistenza interna = 0.27 Ω∗
Amperometro (A2) :
•
•
•
•
Indice di classe n = 0.5
Portata = 1.5 A
Numero di divisioni = 150
Resistenza interna = 39.5 mΩ
∗
La misura della resistenza interna dell’amperometro A1 e A2, non essendo riportata nei dati di targa, è stata effettuata
alimentando l’amperometro e misurando, tramite un millivoltmetro, la caduta di tensione ai suoi capi. Tramite la legge
di Ohm si è poi ricavato il valore della resistenza.
18
Il metodo voltamperometrico
© ing.elettrics_2000/2001