il cavo coassiale nell`approssimazione quasi

6.
Un esempio di applicazione: il cavo coassiale nell’approssimazione quasi-stazionaria
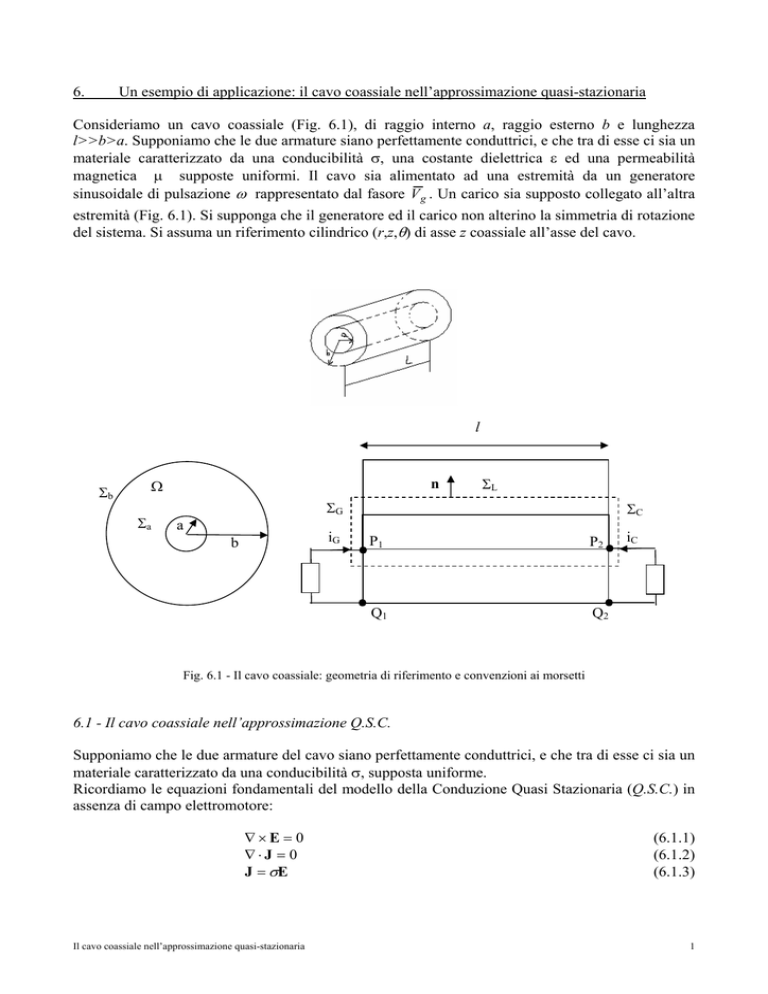
Consideriamo un cavo coassiale (Fig. 6.1), di raggio interno a, raggio esterno b e lunghezza
l>>b>a. Supponiamo che le due armature siano perfettamente conduttrici, e che tra di esse ci sia un
materiale caratterizzato da una conducibilità σ, una costante dielettrica ε ed una permeabilità
magnetica μ supposte uniformi. Il cavo sia alimentato ad una estremità da un generatore
sinusoidale di pulsazione ω rappresentato dal fasore V g . Un carico sia supposto collegato all’altra
estremità (Fig. 6.1). Si supponga che il generatore ed il carico non alterino la simmetria di rotazione
del sistema. Si assuma un riferimento cilindrico (r,z,θ) di asse z coassiale all’asse del cavo.
l
Σb
Ω
Σa
n
ΣL
ΣG
a
iG
b
ΣC
P1
P2
Q1
Q2
iC
Fig. 6.1 - Il cavo coassiale: geometria di riferimento e convenzioni ai morsetti
6.1 - Il cavo coassiale nell’approssimazione Q.S.C.
Supponiamo che le due armature del cavo siano perfettamente conduttrici, e che tra di esse ci sia un
materiale caratterizzato da una conducibilità σ, supposta uniforme.
Ricordiamo le equazioni fondamentali del modello della Conduzione Quasi Stazionaria (Q.S.C.) in
assenza di campo elettromotore:
∇×E = 0
∇⋅J = 0
J = σE
(6.1.1)
(6.1.2)
(6.1.3)
Il cavo coassiale nell’approssimazione quasi-stazionaria
1
Ad esse vanno aggiunte le condizioni di raccordo sulle superfici Σ di discontinuità per la
conducibilità:
E × nˆ Σ continua
(6.1.4)
J ⋅ nˆ Σ continua
(6.1.5)
Sulla superficie di un conduttore perfetto la condizione (6.1.4) si particolarizza come segue:
E × nˆ Σ = 0
(6.1.6)
Sulla superficie che delimita un isolante perfetto, la condizione (6.1.5) diventa
J ⋅ nˆ Σ = 0
(6.1.7)
L’equazione (6.1.1) consente di esprimere il campo elettrico in termini del gradiente della funzione
potenziale φ :
E = −∇φ
(6.1.8)
Notiamo che il segno meno è stato convenzionalmente assunto di modo che il lavoro fatto contro il
campo elettrico per portare una carica unitaria dal punto P∞ all’infinito al punto P lungo la
traiettoria γ rappresenti l’energia potenziale associata alla carica stessa:
P∞
φ ( P) = ∫
P∞γP
( − E) ⋅ dl + φ ( P∞ ) = ∫ E ⋅ dl = ∫ E ⋅ dl
PγP∞
P
In termini della funzione potenziale la formulazione del modello della Conduzione Quasi
Stazionaria è quindi la seguente:
∇ ⋅ σ∇φ = 0
φΣ
nel dominio conduttore
continua
∂φ
continua
∂n Σ
su una superficie Σ di discontinuità per la conducibilità;
φ Σ = φ0 sulla superficie di un conduttore perfetto (condizione di Dirichlet)
σ
∂φ
∂n
= 0 sulla superficie che delimita un isolante perfetto (condizione di Neumann)
Σ
Nel caso in esame, essendo il conduttore omogeneo, il modello della conduzione stazionaria si
riduce alla equazione di Laplace, valida nella regione tra le due armature, con le ulteriori condizioni
al contorno date dalle alimentazioni. Esso risulta quindi espresso dalle
∇ 2φ = 0
φ r =a = V
(6.1.9)
(6.1.10)
φ r =b = 0
(6.1.11)
Per la simmetria risulta φ = φ (r ) e quindi ∇ 2φ =
Il cavo coassiale nell’approssimazione quasi-stazionaria
1 d ⎛ dφ ⎞
⎜r
⎟
r dr ⎝ dr ⎠
2
L’equazione (6.1.9) si riduce pertanto alla seguente
1 d ⎛ dφ ⎞
⎜r ⎟ = 0
r dr ⎝ dr ⎠
che può facilmente essere integrata:
dφ
r
=k
dr
φ = k log r + C
Le costanti si determinano imponendo le condizioni al contorno:
(6.1.12
(6.1.13)
k log a + C = V
k log b + C = 0
Risulta quindi:
φ=−
V
log
r
b
(6.1.14)
b
a
Conseguentemente, la densità di corrente nel mezzo di conducibilità σ ha direzione radiale:
V ˆ
E = −∇φ =
i
(6.1.15)
b r
r log
a
V ˆ
J = σE = σ
i
(6.1.16)
b r
r log
a
log
La corrente che fluisce attraverso una superficie cilindrica S di raggio r risulta quindi:
2π l
2πσl
V
(6.1.17)
b 00
b
S
log
log
a
a
L’applicazione della (6.1.2) in forma integrale alla superficie chiusa di figura dà luogo alla seguente
equazione:
I = ∫∫ J ⋅ nˆ dS = σ
V
1
∫ ∫ r rdθdz =
2πσl
V =0
(6.1.18)
b
log
a
Il cavo coassiale può quindi essere rappresentato in tale caso con un circuito equivalente costituito
da una conduttanza di pari a
− I1 + I 2 +
I 2πσl
=
= gl
(6.1.19)
V log b
a
Considerando il cavo coassiale come un doppio bipolo (Fig. 6.1), utilizzando la definizione (6.1.19)
è possibile immediatamente calcolare i parametri Z, supponendo nota la corrente impressa ai
morsetti dal generatore. Abbiamo infatti:
V 11'
1
Z&11 =
=
(6.1.20)
I 1 I 2 =0 G
G=
Il cavo coassiale nell’approssimazione quasi-stazionaria
3
V 22 '
Z& 22 =
I2
=
I 1 =0
V 22 '
Z& 21 =
I1
=
I 2 =0
1
G
(6.1.21)
1
= Z& 12
G
(6.1.22)
Basta considerare infatti che il bipolo è simmetrico rispetto alle alimentazioni alle due porte. Cioè,
la tensione tra i due elettrodi è la stessa se si alimenta con un generatore di corrente unitario la porta
1 o la porta 2. Risulta quindi Z&11 = Z& 22 . Poiché gli elettrodi sono equipotenziali, la differenza di
potenziale alla porta 2, quando si alimenta la porta 1, è la stessa di quella alla porta 1. Ovviamente
Z&12 = Z& 21 per la reciprocità, come d’altra parte è facile verificare.
Il cavo coassiale si comporta quindi come una resistenza di valore 1/G, come illustrato in Fig. 6.2.
P1
P2
G
Q1
Q2
Fig. 6.2 - Schema equivalente del cavo nell’approssimazione Q.S.C.
Notiamo che la matrice Z&
⎛1 1⎞
⎜
⎟
(6.1.23)
Z& = ⎜ G G ⎟
⎜⎜ 1 1 ⎟⎟
⎝G G⎠
non è invertibile. Non è possibile cioè ottenere, in questo caso, una rappresentazione in termini di
parametri Y& .
6.2 - Il cavo coassiale nell’approssimazione Q.S.E. (
1
τe
<<
1
τ em
<<
1
τm
)
Consideriamo ancora il cavo coassiale descritto precedentemente (Fig. 6.1), di raggio
interno a, raggio esterno b e lunghezza l>>b>a. Supponiamo che le due armature siano
perfettamente conduttrici, e che tra di esse ci sia un materiale dielettrico non perfetto, caratterizzato
da una costante dielettrica ε ed una conducibilità σ, supposte uniformi per il momento.
Introdotto il parametro:
τe =
ε
σ
(6.2.1)
supponiamo che il suo valore (rispetto agli altri tempi caratteristici in gioco) sia tale da farci
concludere, in base a quanto visto in precedenza, che le equazioni da risolvere nel dominio tra le
due armature sia quello dell’elettro-quasi-statica (Q.S.E.).
Ad esempio, supponiamo che il materiale dielettrico interposto tra le armature sia mica
(ε≈5ε0, μ ≈ μ0, σ ≈ 1e-11 S/m), e che la lunghezza sia l ≈ 1m. E’ facile vedere che in questo caso
risulta 1/τem ≈ 1e8 s-1, 1/τe ≈ 0.2 s-1, 1/τm ≈ 8e16 s-1, per cui fino a frequenze di delle decine di MHz
il modello da utilizzare è senz’altro quello Q.S.E.:
Il cavo coassiale nell’approssimazione quasi-stazionaria
4
⎧
⎪ ∇×E = 0
⎪
⎨ ∇⋅D = ρ
⎪ ⎛
∂D ⎞
⎟=0
⎪∇ ⋅ ⎜ J +
∂t ⎠
⎩ ⎝
⎧J = σ E
⎨
⎩D = ε E
⎧⎪E × nˆ Σ = 0
a
⎨
⎪⎩E × nˆ Σ b = 0
(6.2.2)
(6.2.3)
(6.2.4)
Siamo immediatamente in grado di dare un significato fisico al parametro τe introdotto in
(6.2.1). Infatti, sfruttando l’uniformità di ε e σ, combinando le (6.2.2) e (6.2.3) otteniamo
immediatamente:
⎛ ∂D 1 ⎞
∂ρ 1
+ ρ =0
+ D ⎟⎟ = 0 ⇒
∇ ⋅ ⎜⎜
(6.2.5)
∂t τ e
⎝ ∂t τ e ⎠
la cui soluzione si scrive:
−
t
(6.2.6)
ρ (t ) = ρ 0 e
dove ρ0 è il valore della densità di carica all’istante t = 0. Dunque, scopriamo che in un materiale
omogeneo la carica libera decade esponenzialmente a zero con una costante di tempo τe, che
dunque a buon diritto chiamiamo tempo di diffusione delle cariche.
τe
Ci accingiamo ora a risolvere le equazioni scritte, supponendo che la densità di carica libera
ρ sia identicamente nulla. Similmente al caso elettrostatico, possiamo asserire che la prima delle
(6.2.2) (o, meglio, la sua controparte integrale) ci permette di concludere che il campo elettrico può
essere fatto discendere da un potenziale scalare ϕ:
(6.2.7)
E = −∇ϕ
che risulta costante (nello spazio) su Σa e Σb grazie alle (6.2.4), anche se in generale dipendente dal
tempo. Combinando poi le (6.2.2) e le (6.2.3), e sfruttando l’uniformità del mezzo, si ottiene
facilmente:
∂ϕ ⎞
⎛
∇ 2 ⎜ϕ + τ e
⎟=0
∂t ⎠
⎝
(6.2.7)
⎧⎪ϕ Σ = V (t )
a
⎨
⎪⎩ϕ Σb = 0
dove si è arbitrariamente posto a zero il valore del potenziale sull’elettrodo esterno ad ogni istante
di tempo. Ponendo:
∂ϕ
ϕ' = ϕ + τ e
(6.2.8)
∂t
il problema (6.2.7) si riformula come segue:
∇ 2ϕ ' = 0
∂V
⎧
⎪ϕ ' Σa = V ' (t ) = V + τ e ∂t
⎨
⎪ϕ ' = 0
⎩ Σb
Il cavo coassiale nell’approssimazione quasi-stazionaria
(6.2.9)
5
che risulta quindi formalmente identico al problema studiato in precedenza. Facendo l’ipotesi di
simmetria cilindrica (assumendo cioè tutte le grandezze dipendenti solo dalla coordinata radiale r e
non anche da z e θ), la soluzione è pertanto formalmente esattamente la stessa:
r
r
ln
ln
∂
V
⎛
⎞
ϕ ' (t ) = V ' b = ⎜V + τ e
⎟ b
(6.2.10)
a ⎝
a
∂
t
⎠
ln
ln
b
b
Per interpretare fisicamente il risultato, supponiamo che il cavo coassiale sia utilizzato per collegare
due bipoli: un generatore reale ed un carico (Fig. 6.1). Consideriamo la superficie cilindrica Σ
concentrica alle armature e di raggio intermedio, di lunghezza immediatamente maggiore di l.
Dalla legge di conservazione della carica (l’ultima delle (6.2.2)) otteniamo, grazie al teorema della
divergenza:
∂D ⎞
∂D ⎞
⎛
⎛
∇ ⋅⎜J +
⎟ = 0 ⇒ ∫∫Σ ⎜ J +
⎟ ⋅ nˆ dS = 0 ⇒
∂t ⎠
∂t ⎠
⎝
⎝
(6.2.11)
∂D ⎞
∂D ⎞
∂D ⎞
⎛
⎛
⎛
ˆ
ˆ
ˆ
⇒ ∫∫ ⎜ J +
⎟ ⋅ n dS + ∫∫Σ ⎜ J +
⎟ ⋅ n dS + ∫∫Σ ⎜ J +
⎟ ⋅ n dS = 0
ΣG
C ⎝
L ⎝
∂t ⎠
∂t ⎠
∂t ⎠
⎝
Supponendo che su ΣG e ΣC la componente normale di D sia nulla, mentre quella di J sia non nulla
solo in corrispondenza dei cavi di collegamento tra il cavo coassiale e i bipoli, si ottiene
immediatamente:
∂D ⎞
⎛
− i g + iu + ∫∫ ⎜ J +
(6.2.12)
⎟ ⋅ nˆ dS = 0
ΣL
∂t ⎠
⎝
dove l’integrale sulla superficie laterale ΣL si scrive:
∂D ⎞
∂∇ϕ ⎞
∂ϕ '
⎛
⎛
∫∫ΣL ⎜⎝ J + ∂t ⎟⎠ ⋅ nˆ dS = − ∫∫ΣL ⎜⎝ σ∇ϕ + ε ∂t ⎟⎠ ⋅ nˆ dS = − ∫∫ΣL σ∇ϕ '⋅nˆ dS = − ∫∫ΣL σ ∂r dS =
l
2π l
2πl ⎛
dV ⎞
dV (6.2.13)
∂ϕ '
∂V ⎞ 1 1
⎛
rdϑ dz = −2π ∫ σ ⎜V + τ e
r dz =
= −∫ ∫ σ
σV + ε
= GV + C
⎟
⎜
⎟
0
0
0
b
dt ⎠
dt
∂r
∂t ⎠ ln a r
⎝
ln ⎝
b
a
dove
2πlσ
2πlε
G=
= gl , C =
= cl
b
b
(6.2.14)
ln
ln
a
a
sono la conduttanza e la capacità del cavo coassiale, così come studiate nel caso della conduzione
stazionaria e della elettrostatica, rispettivamente.
In definitiva, la (6.2.13) diventa:
dV
− i g + iu + GV + C
=0
(6.2.15)
dt
che si interpreta, in termini di circuito equivalente, come mostrato in Fig. 6.3: il cavo coassiale si
comporta come il parallelo di una conduttanza e di una capacità.
Il cavo coassiale nell’approssimazione quasi-stazionaria
6
P1
P2
C
Q1
G
Q2
Fig. 6.3 - Circuito equivalente del cavo coassiale nell’approssimazione Q.S.E.
Supponiamo ora che l’andamento temporale delle varie grandezze circuitali sia sinusoidale;
introducendo i fasori (indicati con un soprasegno) la (16) diventa:
(6.2.16)
− I G + I C + (G + jωC )V = 0 ⇒ − I G + I C + G (1 + jωτ e )V = 0
dove abbiamo sfruttato il fatto che C/G = τe. Dalla (6.2.16) ritroviamo, nel caso particolare che
stiamo analizzando, il risultato che abbiamo discusso in precedenza in generale: per frequenze
“basse” (tali cioè che ωτe <<1) allora il circuito equivalente diventa praticamente puramente
resistivo, come se le equazioni da risolvere fossero quelle della conduzione stazionaria, mentre per
frequenze più “elevate” (ωτe ≈ 1) allora gli effetti capacitivi diventano importanti o addirittura
preponderanti per ωτe >> 1 (sempre supponendo ωτem << 1). Nel caso numerico discusso
precedentemente, gli effetti resistivi sono rilevanti solo a frequenze più basse di 1Hz, mentre a
frequenze più elevate (fino alle decine di MHz, quando gli effetti propagativi cominciano ad entrare
in gioco) è predominante l’effetto della sola capacità.
Rimaniamo ancora nella situazione di regime sinusoidale, ed analizziamo in questo caso la
situazione di Fig. 6.4: un cavo coassiale, al cui interno ci siano due materiali con diverse
conducibilità e costanti dielettriche σ1, ε1 e σ2, ε2. I due mezzi sono separati da una superficie Σ
cilindrica di raggio c intermedio tra a e b.
L
Ω2
Ω1
Σb
Σa
Σ
b
a
P1 I1
I2 P2
c
Q1
Q2
Fig. 6.4 - Il cavo coassiale con due materiali: geometria di riferimento
In analogia con quanto visto in precedenza, il modello matematico si scrive:
Il cavo coassiale nell’approssimazione quasi-stazionaria
7
⎧∇ ⋅ ((σ 1 + jωε1 )∇ϕ1 ) = 0 in Ω1
⎨
⎩∇ ⋅ ((σ 2 + jωε 2 )∇ϕ 2 ) = 0 in Ω 2
⎧⎪ϕ1 Σ = V
a
⎨
(6.2.17)
⎪⎩ϕ 2 Σb = 0
⎧ϕ1 Σ = ϕ 2 Σ
⎪
⎨
∂ϕ1
∂ϕ 2
⎪(σ 1 + jωε 1 ) ∂r = (σ 2 + jωε 2 ) ∂r
Σ
Σ
⎩
dove le ultime due relazioni si ricavano dalla continuità della componente tangente di E e della
componente normale di J + jωD.
Utilizzando le solite ipotesi di simmetria, si arriva immediatamente a dire che:
⎧ϕ1 = A1 ln r + B1
(6.2.18)
⎨
⎩ϕ 2 = A2 ln r + B2
dove le quattro costanti A1, B1, A2, B2 si calcolano imponendo le condizioni di raccordo e al
contorno:
⎧ A1 ln a + B1 = V
⎪ A ln a + B = 0
2
⎪⎪ 2
(6.2.19)
⎨ A1 ln c + B1 = A2 ln c + B2
⎪
⎪(σ 1 + jωε 1 ) A1 = (σ 2 + jωε 2 ) A2
⎪⎩
c
c
Risolvendo il sistema (6.2.19) si ottiene infine:
⎧
⎡
⎤
r
ln
⎪
⎢
⎥
a
⎪ϕ1 = V ⎢1 −
⎥
⎪
⎢ ln c + (σ 1 + jωε 1 ) ln b ⎥
⎪
a (σ 2 + jωε 2 ) c ⎦⎥
⎣⎢
(6.2.20)
⎨
r
⎪
ln
(
σ 1 + jωε 1 )
⎪
b
⎪ϕ 2 = −V (σ + jωε ) c (σ + jωε ) b
1
2
2 ln
ln
+ 1
⎪
(
a σ 2 + jωε 2 ) c
⎩
A questo punto, possiamo schematizzare il cavo coassiale di Fig. 6.3 in termini di un doppio
bipolo, rappresentato dalla matrice delle impedenze ai morsetti:
⎡V 1 ⎤ ⎡ Z&11 Z&12 ⎤ ⎡ I 1 ⎤
(6.2.21)
⎢ ⎥=⎢&
⎥⎢ ⎥
⎢⎣V 2 ⎥⎦ ⎣ Z 21 Z& 22 ⎦ ⎢⎣ I 2 ⎥⎦
dove, grazie alle proprietà di simmetria e al fatto che le armature sono di conduttore perfetto, si ha
Z& = Z& = Z& = Z& = Z&
11
22
12
21
s
Risulta pertanto:
V1
Z& s =
I1
(6.2.22)
I 2 =0
dove:
Il cavo coassiale nell’approssimazione quasi-stazionaria
8
I1
I 2 =0
= ∫∫ (J + jωD ) ⋅ nˆ dS = − ∫∫ ((σ 1 + jωε1 )∇ϕ1 ) ⋅ nˆ dS = ∫∫ (σ 1 + jωε1 )
Σ
Σ
= (σ 1 + jωε1 ) V 1
Σ
∂ϕ1
dS =
∂r
1c
V1
2πc l =
&
c (σ + jωε1 ) b
Z1 + Z& 2
ln + 1
ln
a (σ 2 + jωε 2 ) c
(6.2.23)
e:
Z& s = Z&1 + Z& 2
1 2πl (σ 1 + jωε1 )
=
= G1 + jωC1
c
Z&1
ln
(6.2.24)
a
2πl (σ 2 + jωε 2 )
1
=
= G2 + jωC2
b
Z& 2
ln
c
dove G1 e C1 (rispettivamente G2 e C2) sono la conduttanza e la capacità di un cavo coassiale di
raggi a e c (rispettivamente c e b).
Ricordando come viene effettuata la sintesi di un doppio bipolo con lo schema a T, in
definitiva il circuito equivalente del cavo coassiale esaminato è quello di Fig. 6.5. Dunque, il
risultato non è semplicemente il parallelo della conduttanza complessiva della struttura (la serie di
G1 e G2) con la sua capacità complessiva (la serie di C1 e C2).
P1
Q1
P2
C1
G1
C2
G2
Z1
Z2
Q2
Fig. 6.5 - Circuito equivalente del cavo coassiale a due materiali
In Fig. 6.6 riportiamo gli andamenti della risposta in frequenza del circuito di Fig. 6.3, in termini di
corrente, paragonato alla soluzione esatta della linea di trasmissione costituita dal cavo coassiale. I
parametri utilizzati sono a=1cm, b=10cm, l=1m, ε=ε0, μ=μ0. La conducibilità σ è stata variata in
modo da ottenere differenti rapporti τem/τe. Possiamo osservare che quando risulta τem/τe << 1 allora
il circuito di Fig. 6.3 dà la risposta corretta, consistentemente con le approssimazioni assunte per
ottenere questo modello.
Il cavo coassiale nell’approssimazione quasi-stazionaria
9
Fig - 6.6: Risposte in frequenza
6.3 - Il cavo coassiale nell’approssimazione Q.S.M. (
1
τm
<<
1
τ em
<<
1
τe
)
Ricordiamo che, in questo caso, assumendo una frequenza relativamente alta (caso 3B della sez. 5),
abbiamo che le equazioni da risolvere sono quelle dell’approssimazione Q.S.M.:
∂B
∇×E = −
(6.3.1)
∂t
(6.3.2)
∇×H = J
∇⋅B=0
(6.3.3)
∇⋅D=ρ
(6.3.4)
con le seguenti relazioni costitutive e condizioni al contorno
Il cavo coassiale nell’approssimazione quasi-stazionaria
10
⎧J = σ E
⎨
⎩D = ε E
⎧⎪E × nˆ Σ
a
⎨
⎪⎩E × nˆ Σ b
[nˆ × H ]Σ a
[nˆ × H ]Σb
(6.3.5)
=0
=0
(6.3.6)
= Ka
(6.3.7)
= Kb
(6.3.8)
Nella (6.3.7) le parentesi quadre []
⋅ Σ indicano la differenza dei valori assunti dal vettore dalle parti
opposte della superficie Σ e K è la densità di corrente superficiale eventualmente presente su Σ .
Devono infine essere specificate le ulteriori condizioni al contorno, conseguenti all’ipotesi di
alimentazione ai morsetti.
Come nei casi precedenti, supponiamo trascurabili gli effetti di bordo.
Notiamo innanzitutto che la (6.3.2) implica la solenoidalità di J. Notiamo inoltre che, per assegnate
sorgenti J, il campo magnetico ha la stessa configurazione ottenuta nel caso della magnetostatica.
Supponiamo di alimentare il sistema come descritto in Fig. 6.1.
Se σ = 0 nel volume tra i due elettrodi, non vi è dubbio che il campo magnetico è lo stesso del caso
magnetostatico. Scegliendo il solito riferimento cilindrico, con asse z lungo l’asse del cavo, si
ottiene allora immediatamente che
(6.3.9)
H = H ϑ (r , t )ˆi ϑ
Applicando la legge di Ampère ad una circonferenza di raggio r, con centro sull’asse z all’ascissa z,
si ha:
I (t )
H ϑ (r , t ) =
(6.3.10)
2πr
dove I(t) è la corrente che fluisce nel cavo. Si noti che in questo caso il campo elettrico può essere
ottenuto considerando la (6.3.1). Tenendo conto che, per la simmetria di rotazione il campo elettrico
non dipende da ϑ si ottiene dalla (6.3.1):
∂Eϑ
(6.3.11)
=0
∂z
∂H ϑ
∂E r ∂E z
(6.3.12)
−
= −μ
∂z
∂r
∂t
1 ∂rEϑ
=0
(6.3.13)
r ∂r
Utilizzando la (6.3.11) e la (6.3.13), nonché le condizioni al contorno (6.3.6), particolarizzate per la
componente ϑ ( Eϑ (a, z , t ) = Eϑ (b, z , t ) = 0 ), si ottiene immediatamente che
Eϑ (r , z , t ) = 0
(6.3.14)
Si ha inoltre che il campo elettrico deve rispettare la (6.3.4) che riscriviamo nel sistema di
coordinate cilindrico, in assenza di densità di carica libera come:
1 ∂rE r ∂E z
+
=0
(6.3.15)
∂z
r ∂r
Una possibile soluzione che rispetti le equazioni (6.3.12) e (6.3.15) è la seguente:
(6.3.16)
E z ( r, z, t ) = 0
dI μz C
+
E r (r , z , t ) = −
(6.3.17)
dt 2πr r
dove C è una costante legata all’alimentazione. Poiché è unica in questo caso la soluzione (il campo
vettoriale E è univocamente determinato in un dominio chiuso dalla conoscenza del suo rotore,
della sua divergenza, delle sue componenti tangenti sul contorno del dominio, e degli integrali di
Il cavo coassiale nell’approssimazione quasi-stazionaria
11
linea tra le parti disgiunte che costituiscono la frontiera del dominio; questi ultimi, nel caso in
esame, tengono conto dei vincoli imposti dalle alimentazioni ai morsetti), il campo elettrico nel
nostro problema è quindi quella data dalle (6.3.14), (6.3.16) e (6.3.17), mentre il campo magnetico
H è espresso dalla (6.3.10).
Se σ ≠ 0 possiamo ragionevolmente supporre che la presenza di una componente di campo elettrico
radiale comporti la nascita di una componente analoga di densità di corrente. Conseguentemente, la
corrente nel cavo non è più uniforme in direzione z. Ipotizziamo pertanto, trascurando sempre gli
effetti di bordo, che anche in questo nuovo caso il campo elettromagnetico abbia solo componenti
traverse rispetto alla direzione z:
(6.3.18)
H = H ϑ ( r, z, t )ˆiϑ
E = E ( r, z, t )ˆi
(6.3.19)
r
r
L’unicità della soluzione, anche in questo caso ci garantirà la correttezza di tale ipotesi di lavoro.
Applicando allora la legge di Ampère ad una circonferenza di raggio r, con centro sull’asse z
all’ascissa z, si ha:
I ( z, t )
H ϑ (r , z, t ) =
(6.3.20)
2πr
dove I(z,t) è la corrente che fluisce nel cavo all’ascissa z. Essendo il campo magnetico ortogonale
all’asse z, non vi è contributo al flusso di B attraverso superfici che giacciono su piani ortogonali a
z. Applicando allora la legge dell’induzione ad una linea chiusa del tipo di quella di Fig. 6.7 si
ottiene:
d
∫γ E ⋅ dl = γ∫ E ⋅ dl + γ∫ E ⋅ dl = − dt ∫∫ B ⋅ ˆi dS = 0 ,
z
A 1B
B
2A
(6.3.21)
Sγ
e quindi:
T Aγ 1B =
∫ E ⋅ dl = TAγ 2 B = −
Aγ 1B
b
∫ E ⋅ dl = V = ∫ Er ⋅ dr
Bγ 2 A
a
A
γ1
γ2
B
Fig. 6.7 – La curva per il calcolo della circuitazione di E
Tenendo anche conto delle (6.3.6), risulta quindi ben definite la tensione V tra i due conduttori.
Chiaramente V = V ( z , t ) in quanto E = E r ( r, z, t )ˆi r .
Le equazioni da risolvere (6.3.1) e (6.3.2) si riscrivono in questo caso nel modo seguente:
Il cavo coassiale nell’approssimazione quasi-stazionaria
12
∂H ϑ
∂E r
= −μ
∂z
∂t
(6.3.22)
∂H
− ϑ = σEr
∂z
(6.3.23)
Integrando entrambi i membri di queste equazioni in r tra a e b è possibile ottenere le equazioni che
devono soddisfare V(z,t) e I(z,t).
Si ha infatti
b
b
∂
∂
E r dr = − μ ∫ H ϑ dr
∫
∂t a
∂z a
b
−
(6.3.24)
b
∂
H ϑ dr = σ ∫ E r dr
∂z ∫a
a
(6.3.25)
e quindi
μ
b ∂I
∂ I ( z, t )
∂V
log
dr = −
= −μ ∫
a ∂t
2π
∂t a 2πr
∂z
b
b
∂ I ( z, t )
∂I 1
b
dr =
log = −σV
∫
∂z a 2πr
∂z 2π
a
Introducendo le definizioni di conduttanza per unità di lunghezza g =
unità di lunghezza l =
μ log
2πσ
e di induttanza per
b
log
a
b
a si ha in definitiva:
2π
∂V
∂I
= −l
(6.3.26)
∂z
∂t
∂I
= − gV
(6.3.27)
∂z
Cerchiamo ora la loro soluzione, nell’ipotesi che le grandezze V ed I abbiano una dipendenza
sinusoidale dal tempo. Passando alla rappresentazione nel dominio dei numeri complessi attraverso
fasori le equazioni (6.3.26)-(6.3.27) diventano:
dV
= − jωl I
dz
dI
= − gV
dz
(6.3.28)
(6.3.29)
e quindi
V =−
1 ∂I
g ∂z
d2I
= jωlg I
dz 2
Il cavo coassiale nell’approssimazione quasi-stazionaria
(6.3.30)
(6.3.31)
13
Poniamo γ 2 = jωlg = jωμσ , δ =
2
ωμσ
, γ = (1 + j )
spessore di penetrazione.
La soluzione della (6.3.31) può essere espressa come
I ( z ) = K 1 e γz + K 2 e − γz
e, dalla (6.3.30)
V ( z) = −
[K e
g
γ
1
γz
− K 2 e −γz
ωμσ
2
=
1+ j
δ
, essendo δ il cosiddetto
(6.3.32)
]
(6.3.33)
Le costanti complesse K 1 e K 2 vanno determinate utilizzando le condizioni al contorno.
Per ottenere un circuito equivalente, bisogna determinare la matrice d’impedenza Z& del doppio
bipolo visto alle due estremità del cavo. Definiamo:
V ( − l)
Z&11 =
I ( − l) I( 0 )=0
(6.3.34)
V( 0 )
&
Z 21 =
I ( − l) I( 0 )=0
dove Z& = Z& per ragioni di simmetria e Z& = Z& per la reciprocità.
22
11
12
21
Per ottenere questi elementi, imponiamo I (−l ) = I g e I (0) = 0 , e valutiamo la tensione alle due
estremità. Abbiamo:
1
K 1 = − K 2 = I g − γl
(6.3.35)
e − e γl
e quindi
e γz − e − γz
I (z) = I g − γl
e − e γl
(6.3.36)
γ e− γz + e γz
V (z) = I g
g e γl − e −γl
Dalla seconda delle (6.3.36) risulta:
γ e γl + e −γl
Z&11 =
(6.3.37)
g e γl − e −γl
2
γ
Z& 21 =
(6.3.38)
γl
g e − e −γl
Sviluppiamo ora la (6.3.37) nel limite ⏐γl⏐ << 1, usando la seguente espansione in serie di Taylor:
e x + e − x = 2 + x 2 + O( x 4 )
e x − e − x = 2 x + O( x 3 )
(6.3.39)
Sostituendo, otteniamo:
e
l
γ 2 + γ 2l 2 1 lγ 2 1
Z&11 ≅
=
+
=
+ jω l
g 2γ l
gl g 2 gl
2
(6.3.40)
1
γ 2
Z& 21 ≅
=
g 2γ l g l
(6.3.41)
Il cavo coassiale nell’approssimazione quasi-stazionaria
14
In conclusione, il circuito equivalente risulta quello mostrato in Fig. 6.8.
I (0)
I (−l )
V (−l )
jω l l/2
jω l l/2
V (0)
gl
Fig. 6.8 - Circuito equivalente del cavo coassiale nell’approssimazione Q.S.M.
Ovviamente, per rendere più valida l’approssimazione utilizzata per ottenere tale circuito
equivalente, si potrebbe suddividere il sistema originale in un numero di parti di lunghezza ridotta,
su ciascuna delle quali l’approssimazione ⏐γl⏐ << 1 è più valida. Risulterebbe un insieme di
circuiti equivalenti come quello di Fig. 6.8 collegati in cascata. In Fig. 6.9 illustriamo il risultato
ottenuto suddividendo in due parti il sistema originario.
I (0)
I (−l )
V (−l )
jω l l/4
jω l l/4
jω l l/4
g l /2
jω l l/4
g l /2
V (0)
Fig. 6.9 - Circuito equivalente del cavo coassiale nell’approssimazione Q.S.M (due celle in cascata)
Si noti che la corrente I(z), nel limite ⏐γl⏐ << 1, considerando, ad esempio, come già fatto le
condizioni di estremità I (−l ) = I g e I (0) = 0 , risulta data dalla
z
I ( z) = −I g
(6.3.42)
l
Utilizzando la (6.3.23), si ottiene infine la densità di corrente che fluisce nel mezzo tra gli elettrodi:
∂H
Ig
Jr = − ϑ =
∂z
2πrl
Questa componente della densità di corrente è costante lungo l’asse del cavo. E’ invece
proporzionale a I (z ) la densità di corrente superficiale su ciascuna delle superfici degli elettrodi.
Il ritardo di gruppo, definito nell’Appendice, ci consente di interpretare il tempo τ m nell’ambito
dell’approssimazione Q.S.M.
In tale limite, infatti, il cavo si presenta come il doppio bipolo di Fig. 6.8. La sua funzione di
trasferimento, nel caso che la porta 2 sia a vuoto, è la seguente
1
gl
− j arctan( ωl 2 )
1
gl
2
H ( jω ) =
e
=
l
1
l
g
+ jω l
1 + (ωl 2 ) 2
2
gl
2
Ricordando che
gl = μσ , τ m = μσl 2
si ha che
β (ω ) = − arctan(
Il cavo coassiale nell’approssimazione quasi-stazionaria
ωτ m
2
)
15
Il ritardo di gruppo è quindi:
t RG = −
Esso è praticamente dato da τ m
dβ
=
dω
τm
1
⎛ ωτ ⎞ 2
1+ ⎜ m ⎟
⎝ 2 ⎠
nel limite Q.S.M., cioè per ωτ m ≤ 1
2
Sviluppiamo infine la soluzione (6.3.36) nel limite ⏐γl⏐ >> 1. Risulta in questo caso: eγl >> e −γl e,
per z<0, e −γz >> e γz .
Pertanto
I ( z) ≅ I g e
−γ ( z + l )
= I ge
−
(1+ j )( z + l )
δ
(6.3.43)
Ritornando nel dominio del tempo:
I ( z, t ) = I g e
−
z +l
δ
sin(ωt −
z+l
δ
)
(6.3.44)
Notiamo che la corrente I(z,t) si propaga in direzione z attenuandosi, L’ampiezza di I(z,t) è
significativamente diversa da zero entro una distanza dal generatore proporzionale allo spessore di
penetrazione δ : la corrente si addensa quindi in prossimità di z=-l (effetto pelle).
In Fig. 6.10 riportiamo gli andamenti della risposta in frequenza del circuito di Fig. 6.8 e 6.9, in
termini di corrente, paragonata alla soluzione esatta della linea di trasmissione costituita dal cavo
coassiale. I parametri utilizzati sono gli stessi del caso precedente. Possiamo osservare che quando
risulta τem/τe >> 1 allora i circuiti di Fig. 6.8 e 6.9 danno la risposta corretta, consistentemente con
le approssimazioni assunte per ottenere questo modello. Osserviamo inoltre che né questo circuito
né il circuito di Fig. 6.3 possono riprodurre la risposta del cavo quando τem/τe = 1, anche per piccolo
valori di ωτem.
Rimuoviamo ora l’ipotesi che il conduttore interno sia un conduttore perfetto. Supponiamo inoltre,
per semplicità , che il conduttore esterno sia ancora perfetto e che tra i due conduttori vi sia il vuoto.
Supponendo che la densità di corrente nel conduttore interno sia diretta lungo z, nasce questa volta
anche una componente di campo elettrico in direzione z. Per simmetria, il campo H sostenuto da
tale corrente risulta ancora diretto lungo ϑ :
J = J z (r , t )ˆi z = σE
(6.3.45)
(6.3.46)
H = H (r , t )ˆi
ϑ
ϑ
In regime sinusoidale le equazioni da risolvere risultano allora:
dEz
= jωμ H ϑ
dr
1 d
−
rH ϑ = J z
r dr
J z =σ Ez
esse possono essere facilmente riscritte come
1 d d
r J z = jωμσ J z
r dr dr
Il cavo coassiale nell’approssimazione quasi-stazionaria
(6.3.47)
(6.3.48)
(6.3.49)
(6.3.50)
16
Hϑ =
dJ z
jωμσ dr
1
(6.3.51)
Fig. 6.10 - Risposte in frequenza
Proviamo a risolverle ipotizzando che la densità di corrente sia pressoché uniforme nel conduttore:
Ig
~
J z ≅ 2 (1 + εJ )
(6.3.52)
πa
con ε << 1
Il cavo coassiale nell’approssimazione quasi-stazionaria
17
Introducendo la variabile adimensionale x =
r
, l’equazione (6.3.50) si riscrive allora nella forma
a
adimensionale:
1 d d
2a 2
~
~
~
2
x (1 + εJ ) = jωμσa (1 + εJ ) = j 2 (1 + εJ )
(6.3.53)
x dx dx
δ
Ricordando il significato del parametro δ , è chiaro che questa situazione corrisponde al limite
a
a2
<< 1 . Allora, ipotizzando che ε ≅ 2 , e trascurando termini di ordine superiore ad ε ,
δ
δ
l’equazione (6.3.53) si riscrive come:
1 d d ~
x J = j2
x dx dx
La soluzione può essere ottenuta per integrazione diretta:
(6.3.54)
x2
~
J = j
+ K 1 log x + K 2
(6.3.55)
2
La condizione che la densità di corrente sia limitata per x che tende a zero richiede necessariamente
che K 1 = 0 . La costante K 2 può essere invece ottenuta imponendo che la corrente totale sia quella
data dal generatore:
2π a
Ig =
a
Ig
πa 2
0
∫ ∫ J z ( r )rdrdϑ =2π ∫
0 0
⎤
⎡ a2
r2
2I g
j
1
(
+
⎢ δ 2 2a 2 + K 2 )⎥ rdr = I g + δ 2
⎦
⎣
⎛ a2
a2 ⎞
⎜⎜ j
⎟
+ K2
2 ⎟⎠
⎝ 8
(6.3.56)
Pertanto
K2 = −j
1
4
(6.3.57)
e
J z (r) =
Ig
πa 2
⎡
a2
1
+
j
⎢
2δ 2
⎣
⎛ r 2 1 ⎞⎤
⎜⎜ 2 − ⎟⎟⎥
2 ⎠⎦
⎝a
(6.3.58)
Il circuito equivalente può essere ottenuto applicando la legge dell’induzione in forma integrale alla
linea chiusa di Fig. 6.11. Si ha
(6.3.59)
∫ E ⋅ dl = − jω ∫∫ B ⋅ nˆ dS = − jωΦ
γ 1 ∪γ 2 ∪γ 3 ∪γ 4
Sγ
e quindi
∫ E ⋅ dl + γ∫ E ⋅ dl + γ∫ E ⋅ dl + γ∫ E ⋅ dl = − jω Φ
B1γ 1 A1
A1 2 A2
A2 3 B2
(6.3.60)
B2 4 B1
0
− V 1 + ∫ E z ( a )dz + V 2 = − jω Φ
(6.3.61)
−l
Notiamo che γ 4 si sviluppa in un conduttore perfetto dove il campo elettrico è nullo.
Sostituendo il valore di E z ( a ) =
J z (a )
σ
che si ottiene utilizzando la (6.3.58), la relazione tra
tensioni e correnti ai morsetti risulta essere
μl ⎞
⎛ l
V1 = Ig⎜
+ jω
⎟ + V 2 + jω Φ
2
8π ⎠
⎝ σπa
Il cavo coassiale nell’approssimazione quasi-stazionaria
(6.3.62)
18
Osservando che
Φ = Lext I g ,
Lext =
b
μl
log
2π
a
(6.3.63)
-l
0
P1
z
P2
γ2
γ1
γ3
γ4
Q1
Q2
Fig. 6.11 - La curva per il calcolo della circuitazione di E
e ponendo
l
μl
; Lint =
2
σπa
8π
si ha la seguente equazione ai morsetti
V 1 = I g R + jωLint I g + jωLext I g + V 2
R=
(6.3.64)
Ad essa corrisponde il circuito equivalente di Fig. 6.12.
P2
P1
R
Q1
Lint
Lext
Q2
Fig 6.12 – Circuito equivalente nel limite di conduttori di conducibilità finita
Consideriamo ora il caso in cui
a
δ
>> 1 . In questa situazione è lecito attendersi che la densità di
corrente si addensa nei pressi della periferia del conduttore identificata da r = a .
E’ conveniente allora esprimere la coordinata spaziale nella seguente forma adimensionale:
r r−a δ
=
+ 1 = 1 + εx
(6.3.65)
a
δ a
r−a
δ
dove x =
ed ε = << 1
a
δ
Il cavo coassiale nell’approssimazione quasi-stazionaria
19
L’equazione (6.3.50) si scrive allora nel modo seguente:
d
d
1
2
a (1 + εx )
Jz = j 2 Jz,
a (1 + εx ) d ( aεx )
d ( aεx )
δ
e quindi:
1
2a 2
d
d
(1 + εx ) J z = j 2 ε 2 J z = j 2 J z
dx
(1 + εx ) dx
δ
(6.3.66)
Trascurando i contributi di ordine ε :
d2
J z = j2 J z
dx 2
(6.3.67)
La soluzione generale di questa equazione differenziale ordinaria omogenea del second’ordine è
J z ( x ) = K 1e − (1+ j ) x + K 2 e (1+ j ) x
(6.3.68)
Sostituendo l’espressione di x in funzione di r
J z ( r ) = K 1e
−(1+ j )
r −a
δ
+ K 2e
(1+ j )
r −a
δ
(6.3.69)
Poichè abbiamo ipotizzato che per r → 0 , J z → 0 , avendo ipotizzato
a
δ
>> 1 , deve risultare
K 1 = 0 . La costante K 2 può essere invece ottenuta ancora una volta imponendo che la corrente
totale sia quella fissata dal generatore:
a
r −a
2π a
(1+ j )
δ a ⎡ (1+ j ) rδ−a ⎤
δ
I g = ∫ ∫ J z ( r ) rdrdϑ = 2π K 2 ∫ e
rdr = 2π K 2
rd ⎢e
⎥=
1 + j ∫0 ⎣
0 0
0
⎦
2π K 2
Nel limite
a
δ
δ ⎡
⎢re
1+ j ⎢
⎣
(1+ j )
δ
a
−∫e
0
(1+ j )
r −a
δ
0
⎤
δ
dr ⎥ = 2π K 2
1+
⎥⎦
⎡
δ
⎢a −
j ⎣⎢
1+
a
− (1+ j ) ⎞ ⎤
⎛
δ ⎟
⎜1 − e
⎟⎥
j ⎜⎝
⎠⎦⎥
>> 1 :
I g ≅ 2π K 2
e quindi:
r −a a
δa ⎡
δ 1
1−
⎢
1+ j ⎣ a 1+
1+ j
2πδa
r −a
1 + j (1+ j ) δ
J z (r) = I g
e
2πδa
K2 = I g
⎤
δa
≅ 2π K 2
⎥
j⎦
1+ j
(6.3.70)
(6.3.71)
Il circuito equivalente si ottiene con considerazioni analoghe alle precedenti, sostituendo il nuovo
J z (a )
1+ j
valore di E z ( a ) =
= Ig
nella (6.3.61). In questo caso la relazione tra tensioni e
σ
σ 2πδa
correnti ai morsetti risulta essere
Il cavo coassiale nell’approssimazione quasi-stazionaria
20
l
⎛ l
V1 = Ig⎜
+ j
σ 2πaδ
⎝ σ 2πaδ
⎞
⎟ + V 2 + jωLext I g
⎠
(6.3.72)
Ponendo
l
σπaδ
si ha la seguente equazione ai morsetti
(6.3.73)
V 1 = I g R + jX I g + jωLext I g + V 2
Ad essa corrisponde un circuito equivalente ancora analogo a quello di Fig. 6.12. In questo caso
però nel calcolo della resistenza compare una sezione equivalente pari a 2πaδ , che evidenzia come
la sezione utile al passaggio di corrente è ridotta ad una corona circolare di spessore δ . Notiamo
anche che, in questo caso la resistenza e l’induttanza sono funzioni della frequenza a causa della
presenza del parametro δ .
R=X =
6.4 - Il cavo coassiale nell’approssimazione Q.S.E.M. (
1
1
1
≈
≈
)
τ m τ em τ e
In questo caso, le equazioni da risolvere sono le equazioni di Maxwell nella loro forma completa,
che, nel nostro caso, con passaggi analoghi a quelli sviluppati in precedenza, possono essere
riscritte nel modo seguente:
dV
= − jωl I
dz
dI
= −( g + jωc )V
dz
dove
g=
(6.4.1)
(6.4.2)
2πε
b
μ
2πσ
, l=
log , c =
b
b
2π
a
log
ln
a
a
Queste sono le equazioni standard delle linee di trasmissione, che risolviamo con le seguenti
condizioni ai limiti:
V (−l ) = V g
(6.4.3)
I (0) = 0
Con le manipolazioni usuali otteniamo:
d 2V
(6.4.4)
− (ω 2 LC − jωLG )V = 0
dz 2
e quindi
V = V+ e − jβz + V− e jβz
1
(6.4.5)
I =
(V+ e − jβz − V− e jβz )
Z0
con:
1
, Re β > 0
β = ω 2 LC − jωLG = ω 2 με − jωσμ = ω με 1 − j
(6.4.6)
ωτ e
Il cavo coassiale nell’approssimazione quasi-stazionaria
21
Z0 =
ωL
β
Applicando le condizioni ai limiti, otteniamo:
(e − jβz + e jβz )
V (z) = Vg jβl
(e + e − jβl )
Vg ( e − jβz − e jβz )
I (z) =
Z 0 (e jβl + e − jβl )
(6.4.7)
Poichè siamo sempre nel caso in cui ωτ em << 1 ⇒ ⏐β l⏐<<1, possiamo applicare sulla soluzione
(6.4.7) tutte le approssimazioni del caso precedente (vedi relazioni (6.3.39)), ottenendo il circuito
equivalente di Fig. 6.13.
I (−l ) jω l l/2
jω l l/2
jω c l
gl
V (−l )
I ( 0)
V ( 0)
Fig - 6.13. Il circuito equivalente nell’approssimazione Q.S.E.M.
Ovviamente, anche in questo caso possiamo dividere il sistema in due parti ed ottenere la cascata di
due circuiti come quello di Fig. 6.13.
In Fig. 6.14 riportiamo gli andamenti della risposta in frequenza del circuito ottenuto con due celle a
T, paragonato alla soluzione esatta della linea di trasmissione costituita dal cavo coassiale, ed ai
risultati ottenuti con i due circuiti equivalenti precedenti. I parametri geometrici sono gli stessi dei
casi precedenti. Possiamo osservare che questo circuito è in grado di riprodurre correttamente i
risultati anche quando τem/τe = 1, come atteso.
Il cavo coassiale nell’approssimazione quasi-stazionaria
22
Fig. 6.14 - Risposte in frequenza
[1] H. A. Haus, J. R. Melcher, Electromagnetic fields and energy, Prentice Hall, Englewood Cliffs,
New Jersey, 1989.
[2] L. De Menna, G. Miano, Unpublished
Il cavo coassiale nell’approssimazione quasi-stazionaria
23
Appendice
Ritardo di gruppo
Vogliamo determinare il tempo impiegato perché il segnale attraversi un doppio bipolo, nel caso
limite che il segnale sia sinusoidale di pulsazione ω . Il ritardo nella trasmissione non può che
essere associato ad una localizzazione temporale del segnale, cosa non evidenziabile nel caso del
segnale sinusoidale. Per poter effettuare tale valutazione risulta allora conveniente supporre il
segnale d’ingresso costituito da due sinusoidi di pulsazione quasi uguale, cioè:
v g (t ) = cos(ω − Δω )t + cos(ω + Δω )t
(A.1)
Vediamo che tale segnale è equivalente a
v g (t ) = 2 cos Δωt cos ωt
(A.2)
L’ampiezza del segnale risulta in questo caso modulata dalla cosinusoide di pulsazione Δω ,
pervenendo così ad una implicita localizzazione del segnale di pulsazione ω . In particolare, con la
modulazione abbiamo acquisito, in un certo senso, un riferimento temporale che vede il massimo
del segnale in t=0. Il segnale sinusoidale iniziale si riottene nel limite Δω → 0 .
Supponiamo che la funzione di trasferimento del doppio bipolo sia H ( jω ) = A(ω )e jβ (ω ) .
Conseguentemente il segnale sinusoidale in uscita vu(t), può essere ottenuto, passando alla
rappresentazione con i fasori:
V u ( j (ω − Δω )) = H ( j (ω − Δω ))V g ( j (ω − Δω )) = H ( j (ω − Δω ))
V u ( j (ω + Δω )) = H ( j (ω + Δω ))V g ( j (ω + Δω )) = H ( j (ω + Δω ))
e sovrapponendo nel dominio del tempo le uscite ottenute alle frequenze ω − Δω ed ω + Δω :
vu (t ) = A(ω − Δω ) cos[(ω − Δω )t + β (ω − Δω )] + A(ω + Δω ) cos[(ω + Δω )t + β (ω + Δω )] (A.3)
Nel limite Δω → 0 , possiamo scrivere:
A(ω ± Δω ) = A(ω ) ±
dA
Δω
dω ω
(A.4)
β (ω ± Δω ) = β (ω ) ±
dβ
Δω
dω ω
(A.5)
Sostituendo le (A.4)-(A.5) nella (A.1) si ha:
⎧ ⎡
⎤
⎡
dβ
dβ ⎤ ⎫
Δω )⎥ + cos ⎢ωt + β (ω ) + Δω (t +
) ⎬+
vu (t ) = A(ω ) ⎨cos⎢ωt + β (ω ) − Δω (t +
dω ω
dω ω ⎥⎦ ⎭
⎦
⎣
⎩ ⎣
⎧
⎡
⎤
⎡
dβ
dβ ⎤ ⎫
dA
Δω ⎨− cos⎢ωt + β (ω ) − Δω (t +
Δω )⎥ + cos ⎢ωt + β (ω ) + Δω (t +
) ⎬=
dω ω
dω ω
dω ω ⎥⎦ ⎭
⎣
⎦
⎣
⎩
⎡
⎡
dβ ⎤
dA
dβ ⎤
2 A(ω ) cos⎢ Δω (t +
)⎥ cos[ωt + β (ω )] − 2
Δω sin ⎢ Δω (t +
) sin[ωt + β (ω )]
dω ω ⎦
dω ω
dω ω ⎥⎦
⎣
⎣
(A.6)
Trascurando il secondo termine nel limite Δω → 0 si ha infine:
⎡
dβ ⎤
vu (t ) = 2 A(ω ) cos ⎢ Δω (t +
)⎥ cos[ωt + β (ω )]
d
ω
ω
⎣
⎦
Il cavo coassiale nell’approssimazione quasi-stazionaria
(A.7)
24
Vediamo, anche con riferimento alla Fig. A.1, che il segnale in uscita raggiunge il suo valore
β
dβ
massimo per t DG = −
, mentre il massimo del segnale sinusoidale si ottiene per t DF = − . Il
dω ω
ω
tempo tDG definisce il cosiddetto ritardo di gruppo, mentre il tempo tDF corrisponde al ritardo di
fase. E’ il ritardo di gruppo la grandezza che consente di valutare il tempo di transito del segnale
attraverso la rete due porte.
Fig. A.1 – Andamenti delle tensioni in ingresso ed in uscita ad un doppio bipolo e valutazione del ritardo di fase e di
gruppo.
Il cavo coassiale nell’approssimazione quasi-stazionaria
25