Esercizi di laboratorio in astronomia. Variabili cefeidi e scala di distanza cosmica
Il mezzo più accurato per determinare le distanze dalle stelle più vicine è conosciuto come
parallasse trigonometrica. Questo implica la misurazione dello spostamento angolare di una stella
rispetto ad oggetti molto più remoti, visto da diverse posizioni dell’orbita terrestre. La distanza di
una stella in parsec (1 parsec = 3,26 anni luce) equivale all’inverso della sua parallasse in
secondi di arco. Ciascuna determinazione di parallasse contiene come regola un errore probabile
di circa 0,005 secondi. E’ evidente che, poiché gli scienziati cercano di determinare le distanze di
stelle sempre più remote, la parallasse trigonometrica dà risultati sempre meno precisi o accurati.
Ad una distanza di 200 parsec, l’errore probabile risulta ampio quanto la parallasse stessa.
Nonostante il successo dei moderni astronomi di diminuire gli errori delle determinazione di
parallasse, questo metodo di determinare le distanze stellari risulta affidabile solo per gli oggetti
che entrano nel “campo” dell’orbita solare.
Si richiedono altri metodi per gli oggetti più distanti di alcune centinaia di parsec.
In questo esercizio utilizzeremo le stelle variabili cefeidi, quelle che cambiano in luminosità nei
periodi da 1 a 100 giorni secondo la modalità della variazione nell’arco di 4-5 giorni di cefei d.
Alcune di queste stelle supergiganti sono 10.000 volte più luminose del nostro sole e per questo
possono essere viste a grande distanza, essendo riconoscibili e distinguibili nelle galassie più
vicine. Le Cefeidi giocarono un ruolo chiave nei primi anni di questo secolo nel fornire la prova che
esistono altre galassie oltre la nostra. Sebbene oggi noi siamo assolutamente a conoscenza che
esistono altre galassie oltre la nostra Via Lattea, quest’idea non era comunemente accettata prima
del 1920.
Variabili cefeidi
La prima variabile cefeide scoperta nel 1784 fu la Cefeide d grazie ad un astronomo amatore
inglese John Goodricke. Attorno al 1879 A. Ritter teorizzò che le variazioni della luce di queste
stelle sono dovute a pulsazioni : la stella si espande e si contrae alternativamente. Più tardi gli
astronomi verificarono questa idea attraverso le osservazioni spettroscopice. In questo esercizio
noi non ci preoccupiamo di capire il perché una stella pulsa, ma piuttosto vogliamo capire come
esse possano essere utilizzate come indicatori di distanza.
All’inizio di questo secolo la distanza della Piccola Nube di Magellano ( riconosciuta come una
galassia vicina) era sconosciuta . IN alcune foto di questa galassia all’Osservatorio di Harvard, H.
S. Leavitt scoprì molte cefeidi deboli. Nel 1912 ella dimostrò, in un suo studio dettagliato di circa
due dozzine di queste cefeidi, che esisteva una stretta correlazione tra le magnitudini apparenti e
i periodi di queste stelle nel senso che ad un più lungo periodo corrispondeva una maggiore
luminosità delle stelle.
Poiché tutte le stelle della Piccola Nube di Magellano si trovano essenzialmente alla medesima
distanza dal sole, ne consegue che le Cefeidi apparentemente più luminose presenti in essa siano
di fatto intrinsecamente ancora più luminose. In altre parole il periodo di una cefeide è un
indicatore della sua luminosità intrinseca e nel problema successivo utilizzeremo questa proprietà
per determinare la distanza della Piccola Nube di Magellano
Prima tappa
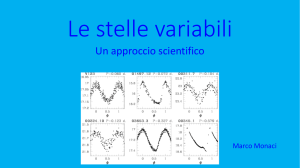
Sulla pagina seguente vengono mostrate le curve/scie di luce di quattro variabili cefeidi nella
Piccola Nube di Magellano attraverso delle osservazioni fotografiche ad opera di H. C. Arp sotto la
luce gialla. Per ogni stella deduci la magnitudine apparente al picco e al minimo della più vicina
magnitudine 0.1: poi prendi la media di questi due valori. Inoltre, per ogni stella, trovate il suo
periodo in giorni partendo dall’intervallo tra massimi successivi. Prendete il logaritmo del periodo
fino alla seconda cifra decimale.
Sul grafico alla pagina seguente, per ogni stella, indicate la magnitudine apparente media in
ordinata rispetto al logaritmo del periodo. Per aumentare il numero di punti, riportate i dati della
Tavola I, che sono validi anche per le Cefeidi della Piccola Nube osservate in una luce gialla da
Arp. In seguito, disegnate una linea retta che unisca i punti relativi ai dati nel miglior modo
possibile. Questa grafico ci mostra la relazione tra la magnitudine apparente e il periodo delle
Cefeidi in quella galassia. Poiché tutte le stelle nella Piccola Nube si trovano essenzialmente alla
stessa distanza da noi, il grafico può anche essere considerato come una relazione periodoluminosità (P-L) che non è ancora stata calibrata. Procediamo ora alla calibrazione, in base a
quanto descritto nella pagina seguente.
CALIBRAZIONE DI SHAPLEY
Se due stelle hanno la stessa luminosità intrinseca, la loro brillantezza apparente è inversamente
proporzionale al quadrato della loro distanza. Questo semplice fatto può essere riconfermato con
una formula che connette la magnitudine apparente m di una stella e la sua distanza d in parsecs
con la magnitudine assoluta M della stessa stella (definita come la magnitudine che essa avrebbe
se fosse vista da una distanza standard di 10 parsecs).
Questa formula è
M = m + 5 – 5 log d.
(1)
Quindi, se conosciamo la magnitudine assoluta e apparente di qualsiasi stella, possiamo calcolare
la sua distanza con questa formula. Allo stesso modo, se la relazione P-L può essere calibrata in
termini di magnitudine assoluta (anziché di magnitudine apparente come era solita fare Miss
Leavitt nel 1912), allora la conoscenza di un periodo di una Cefeide ci fornirebbe la sua distanza,
poiché l’unica altra quantità necessaria è la magnitudine apparente e quest’ultima è facilmente
osservabile.
In 1918 Harlow Shapley fornì una calibrazione, in seguito leggermente rivista da lui stesso, che
divenne largamente accettata dagli astronomi. La Tabella II mostra la relazione P-L di Shapley,
con magnitudini visive assolute per alcuni valori del logaritmo del periodo.
Bisognerebbe sottolineare che qualsiasi calibrazione di quel tipo è molto difficile da realizzare.
Persino la Cefeide più vicina nella nostra galassia è troppo lontana per poter determinare la sua
distanza attraverso il metodo trigonometrico della parallasse. Tuttavia, le informazioni statistiche
riguardanti le distanze delle Cefeidi più luminose possono essere ricavate dai loro moti
osservabili.
La maggior parte delle Cefeidi utilizzate da Shapley si trovavano in ammassi globulari nella Via
Lattea.
FASE 2
Riportate i dati di Shapley sullo stesso grafico di Arp, ma usando la scala destra sull’asse delle
ordinate(y), questa volta in termini di magnitudine assoluta M. Disegnate una linea retta che
unisca i punti. Questa è la relazione calibrata P-L che per molti anni è stata usata per determinare
le distanze verso oggetti contenenti Cefeidi. La linea attraverso i dati di Shapley dovrebbe essere
quasi parallela a quella di Arp.
Determinate la differenza verticale m – M tra le due curve in varie posizioni (per ridurre l’effetto di
qualsiasi piccola differenza di pendenza) e prendete la media. Partendo da questa differenza m –
M, conosciuta come modulo di distanza, usate l’equazione (1) per calcolare la distanza verso la
Piccola Nube Magellanica.
La CALIBRAZIONE DI BAADE
Nel 1923, Edwin Hubble all’Osservatorio del Monte Wilson riuscì a trovare 12 Cefeidi nella
nebulosa di Andromeda (M31) e 22 nella grande nebulosa del Triangolo (M33). Usando
essenzialmente lo stesso metodo che voi avete appena applicato, Hubble riuscì a rilevare una
distanza di circa 285,000 parsecs per M31. Una tale distanza chiariva il fatto che la nebulosa di
Andromeda e sistemi simili erano grandi aggregati di stelle, paragonabili a pieno diritto alla nostra
Via Lattea. Alcuni anni dopo, gli astronomi realizzarono che le polveri stellari nella via lattea
oscuravano anche le altre galassie, oltre alla nostra, facendole apparire troppo lontane.
A causa di ciò la distanza di M31 è stata modificata verso il basso ed è stata
generalmente accettata una cifra di 230.000 parsec. Inoltre le distanze verso
le altre galassie sono state determinate dalla relazione calibrata P-L di
Shapley. Quindi la scala di distanza dell'universo si è basata sul lavoro di
Shapley.
Ma come vedremo ora, queste distanze sono state seriamente sottovalutate. Una
revisione di maggiore importanza è stata fatta nel 1952 da W. Baade, dalla
prima foto della galassia Andromeda fatta con il nuovo telescopio Palomar da
200 pollici ( =cm.2,54 ).
Baade aveva precedentemente scoperto che le stelle si possono sostanzialmente
dividere in due categorie d'età. Le stelle Population I sono relativamente
giovani, calde, e si trovano tipicamente nel braccio a spirale delle galassie,
mentre le stelle Population II sono antiche e si trovano caratteristicamente
negli ammassi globulari e negli aloni delle galassie. Nelle sue foto del 1952
dell'M31 con il telescopio da 200 pollici, Baade scoprì che solo le stelle più
brillanti della Population II potevano essere fotografate, sebbene ci si
aspettasse che apparissero quelle più pallide. Questo dimostrò che la galassia
Andromeda dovesse essere ancora più distante di quanto si credeva
precedentemente.
Sebbene non riuscì a trovare Cefeidi negli ammassi globulari di M31, ma molti
nei bracci a spirale, dedusse che le Cefeidi nei globulari devono essere la
Population II e che le Cefeidi nel braccio a spirale fossero la Population I.
Insieme a ciò ci si accorse che le Cefeidi degli ammassi globulari , usate da
Shapley nella sua relazione di calibratura P-L, dovessero essere circa 1,5 di
magnitudo più pallide delle Cefeidi osservate da Miss Levitt nelle Nuvole
Magellaniche, che sono della Population I. L a scoperta portò ad una revisione
della scala di distanza extragalattica di un fattore leggermente superiore a
due. Sebbene fosse popolarmente accettato che l'universo era diventato "due
volte più grande", naturalmente erano solo i valori numerici delle distanze che
cambiavano.
STEP 3
Calcolate la distanza revisionata dalla Piccola Nuvola Magellanica che
risulta se il modulo di distanza è cambiato di -1,5 magnitudo.
UNA CALIBRATURA ALTERNATIVA
Persino dopo il contributo di Baade, potrebbe essere necesssaria una ulteriore
revisione alla relazione P-L. Il problema fondamentale rimane, come al tempo di
Shapley, la determinazione del punto zero della relazione P-L. C'è ancora
incertezza riguardo all'accuratezza dei metodi statistici che Shapley era
solito usare per dedurre le distanze delle Cefeidi dai loro moti. Inoltre, gli
astronomi moderni hanno cercato altri mezzi di osservazione per stabilire il
punto zero.
Nel 1961 R. Kraft all'Osservatorio di Lick ha dedotto le magnitudo assolute di
sei Cefeidi della Population I che facevano parte di ammassi aperti, che sono
anche della Population I e le cui distanze si possono trovare in altri modi..
Di per sè queste sei stelle sono insufficienti per definire completamente il
punto zero e l'inclinazione della curva. Ma determinando i colori intrinsechi
di queste sei stelle, Kraft fu in grado di estendere la sua lista fino ad
includere altre 26 Cefeidi non associate con alcun ammasso. Una selezione delle
32 Cefeidi viene fornita nella Tabella III, con un asterisco affisso alle sei
che sono negli ammassi aperti.
STEP 4
Nello stesso grafico che contiene il lavoro di Arp e Shapley, traccia anche i
valori di M e registra P dalla Tabella III. Poi disegna la linea retta che
meglio si adatta a questi punti. Come prima, determina il modulo di distanza
m - M per la Piccola Nuvola Magellanica e calcola la distanza da ( 1 ).
SVILUPPI FUTURI
Sebbene le variabili Cefeidi continuino ad essere potenti indicatori della
scala di distanza cosmica, gli astronomi ora sono propensi a credere che le
Cefeidi in una galassia non possono essere fisicamente identiche a quelle dello
stesso periodo in un'altra galassia. L'inclinazione della relazione P-L può
essere diversa da una galassia a quella seguente, a seconda della relativa
abbondanza degli elementi in ciascuna di esse.
Inoltre, anche se la scala di distanza è conosciuta più accuratamente oggi di
quanto non fosse al tempo di Shapley, dobbiamo attendere osservazioni
aggiuntive e i modelli teorici delle variabili delle Cefeidi prima che gli
astronomi possano valutare quanto accurata essa sia.
Tabella pag. 242
Le variazioni di luce delle quattro stelle variabili Cefeidi nella Piccola Nube Magellanica vengono mostrate
in questo grafico per essere usate nella Fase I di questo esercizio in laboratorio. Queste curve sono basate
su osservazioni fotografiche effettuate nella luce gialla da Halton C. Arp, usando un rifrattore da 46 cm in
Sud Africa. La sua scala di magnitudine è stata calibrata fotoelettricamente e quindi è particolarmente
affidabile. Le lettere HV indicano una stella variabile scoperta dagli astronomi dell’Ossevatorio di Harvard.
La grande maggioranza della variabili nella Piccola Nube sono state scoperte trovate su fotografie
effettuate con telescopi di Harvard in Peru e in Sud Africa.
Griglia pag. 243
Questa griglia, o un suo equivalente, serve per disegnare il grafico di questo esercizio. Notate che la scala
della magnitudine apparente a sinistra e la scala della magnitudine assoluta a destra sono completamente
indipendenti.