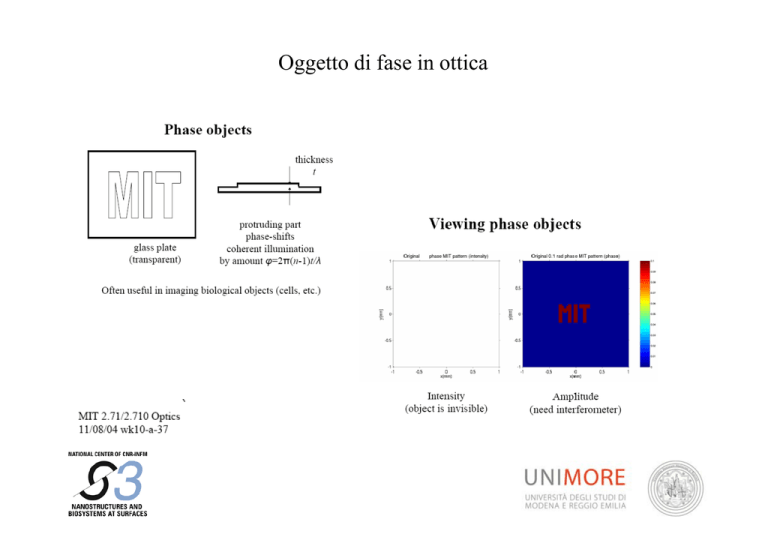
Oggetto di fase in ottica
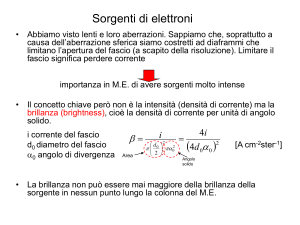
PB: Come trasformare l’informazione contenuta nella FASE
dell’onda trasmessa in CONTRASTO DI INTENSITA’
osservabile?
•Filtraggio
Filtraggio spaziale
•Piatto di fase (OTTICA)
•Interferenza
•Olografia
Contrasto e
risoluzione
Teoria di ABBE e filtraggio spaziale
Funzione di trasferimento
del contrasto di fase
(ampiezza) ideale
Diffraction
Image mode
from Williams, Carter
“Transmission electron
microscopy”
10 nm
CTEM and Selected Area Electron Diffraction
(SAED)
10 nm
2d hkl sin(θ B ) = λ : legge di Bragg
transmitted
beam
d hkl sin( 2θ B ) = λ
D hkl
L
2
⎤
λL ⎡ 3 ⎛ D hkl ⎞
⎢1 + ⎜
=
⎟ + .....⎥
D hkl ⎢ 8 ⎝ L ⎠
⎥⎦
⎣
sin( 2θ B ) ≈ tan(2θ B ) ≈ 2θ B ≈
d hkl
Δd hkl
≈ 0.001 − 0.01
d hkl
C
T
E
M
10 nm
Contrasto di ampiezza prodotta
dal diaframma di obiettivo
Si
Ni
C
10 nm
hole
Low resolution (~1nm)
imaging
Introduction to Electron
Microscopy and Microanalysis
Vick Guo 1985
Teoria di ABBE e filtraggio spaziale
Funzione di trasferimento
del contrasto di fase
ideale
g( x ) = e iΦ ( x ) ≈ 1 + iΦ ( x ) a meno di termini quadratici
2
1 + iΦ ( x ) = 1 + Φ 2 ( x ) ≈ 1
Zernike phase plate
a meno di termini quadratici
Ma se si riesce a moltiplicare per i o la parte diffratta dall' oggetto Φ ( x ),
(o quella trasmessa) si ha :
2
1 − Φ ( x ) = 1 − 2Φ ( x ) + Φ 2 ( x ) ≈ 1 − 2Φ ( x ) a meno di termini quadratici
Nel piano FOCALE della lente obiettivo:
g (u ) = F(g ( x )) = δ (u ) + iF(Φ ( x ))
g ⊗ (u ) = δ (u ) + iiF(Φ ( x )) = (δ (u ) − F(Φ ( x ) )
Nel piano IMMAGINE della lente obiettivo:
F −1 (g ⊗ (u )) = 1 − Φ ( x )
2
I = 1 − Φ ( x )) = (1 - 2Φ ( x ) + Φ 2 ( x )) ≈ 1 − 2Φ ( x )
Immagini a risoluzione atomica
1
λ3
⎛1⎞ 1
χ ⎜ ⎟ = πC s 4 + πΔfλ 2
d
d
⎝d ⎠ 2
Optimum defocus (Scherzer defocus )Δf :
Δ f = − 1 . 2 (λ C s
)1 / 2
~ 43 nm
for optimum resolution
Si monocristallino: direzione cristallografica di incidenza [110]
Immagine
Simulazione
i
interferenziale
f
i l a
risoluzione atomica
Potenziale
Diffrazione
(2‐20)
(1‐1‐1)
(1
1 1)
Funzione
d’onda
(1‐11)
(1
11)
Immagine
(000)
(00‐2)
((002))
(‐11‐1)
(‐111)
( 220)
(‐220)
0.5431nm
Immagini HREM direttamente interpretabili
(debole oggetto di fase)
interfaccia amorfo-cristallo
i
interfaccia
f i eterostruttura semiconduttore
i d
Parte lab:
Il microscopio ottico a proiezione come modello
per introdurre la microscopia elettronica in
trasmissione
Contrasto e
risoluzione
Teoria di ABBE e filtraggio spaziale
Funzione di trasferimento
del contrasto
Il microscopio ottico
a proiezione
Il microscopio elettronico
in trasmissione
Source plane
Diffraction plane
Lente sottile: piano focale e piano immagine
1/ d = u
u=
u=
i αx
sin
λ
sin α
λ
,v =
sin α y
λ
MICROSCOPIO OTTICO A PROIEZIONE:
Filtraggio
gg spaziale
p
Figura di diffrazione
(O)
(A)
I
Immagine
i del
d l Campione
C
i
a)
b)
c)
Immagine ottenuta selezionando solo
il massimo centrale (O)
Immagine ottenuta selezionando solo
un massimo secondario
Immagine ottenuta con il massimo centrale (O) e il massimo A.
I hkl = js
2π 2 m 2 e 2
h
4
2 2
KNVcp hkl Vg λ d hkl
js densità di corrente, K: numero di cristalli densità di corrente K: numero di cristalli
con N celle unitarie, Ve volume di una cella unitaria, phkl: molteplicità del piano hkl, Vg: fattore di struttura, λ lunghezza d
fattore di struttura, λ
lunghezza d’onda,
onda, d
dhkl
spaziatura dei piani.
IMMAGINI TEM DI Al POLICRISTALLINO:
DIFFRAZIONE
IMMAGINI TEM DI Al POLICRISTALLINO:campo chiaro
senza diaframma di obj.
obj.
con diaframma di obj.
obj. sul centrale
0.2μm
Modalità Diffrazione
Modalità Immagine senza
diaframma di obiettivo
Selezionando il massimo centrale e i primi ordini di diffrazione il TEM,
Filtraggio spaziale e alta risoluzione
lavora in “Modalità di funzionamento Bright
g Field Alta Risoluzione”
Grazie per l’attenzione
Grazie per l
attenzione
Aberrations and phase shifts
Formazione
dell’immagine in contrasto di
fase: Teoria di Abbe
f ( x , y) = exp[iσVp ( x , y)]
≈ 1 + iσVp ( x , y)
H
R
E
M
• e − iχ ( u , v ) • A ( u , v )
I( x , y) = 1 + 2σVpabb ( x , y)