Macchina sincrona isotropa

Macchina sincrona isotropa: note aggiuntive 1. Teoria e costruzione di Potier per la macchina sincrona isotropa in saturazione
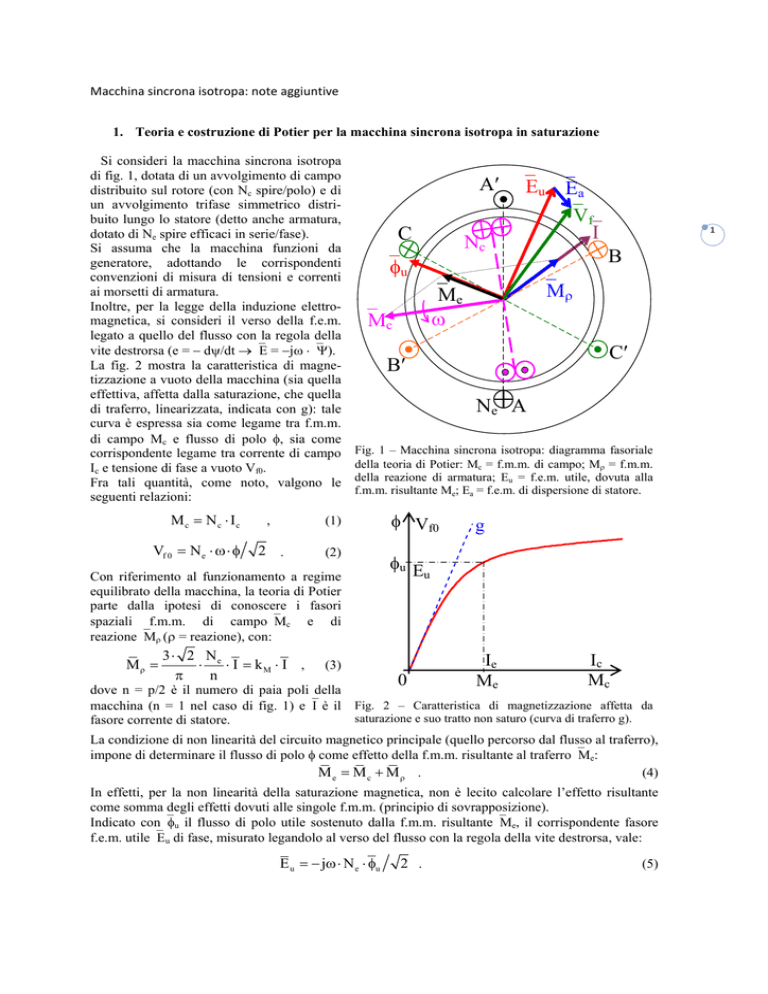
Si consideri la macchina sincrona isotropa
di fig. 1, dotata di un avvolgimento di campo
distribuito sul rotore (con Nc spire/polo) e di
un avvolgimento trifase simmetrico distribuito lungo lo statore (detto anche armatura,
dotato di Ne spire efficaci in serie/fase).
Si assuma che la macchina funzioni da
generatore, adottando le corrispondenti
convenzioni di misura di tensioni e correnti
ai morsetti di armatura.
Inoltre, per la legge della induzione elettromagnetica, si consideri il verso della f.e.m.
legato a quello del flusso con la regola della
vite destrorsa (e =  d/dt E = j ).
La fig. 2 mostra la caratteristica di magnetizzazione a vuoto della macchina (sia quella
effettiva, affetta dalla saturazione, che quella
di traferro, linearizzata, indicata con g): tale
curva è espressa sia come legame tra f.m.m.
di campo Mc e flusso di polo , sia come
corrispondente legame tra corrente di campo
Ic e tensione di fase a vuoto Vf0.
Fra tali quantità, come noto, valgono le
seguenti relazioni:
M c  N c  Ic
Vf 0  N e   
,
(1)
2 .
(2)
C
u
3  2 Ne

 I  kM  I ,

n
1
B
M
Me

Mc
C
B
Ne A
Fig. 1 – Macchina sincrona isotropa: diagramma fasoriale
della teoria di Potier: Mc = f.m.m. di campo; M = f.m.m.
della reazione di armatura; Eu = f.e.m. utile, dovuta alla
f.m.m. risultante Me; Ea = f.e.m. di dispersione di statore.
Con riferimento al funzionamento a regime
equilibrato della macchina, la teoria di Potier
parte dalla ipotesi di conoscere i fasori
spaziali f.m.m. di campoMc e di
reazioneM ( = reazione), con:
M 
A Eu Ea
Vf
I
Nc
(3)
 Vf0
g
u E
u
0
Ie
Me
Ic
Mc
dove n = p/2 è il numero di paia poli della
macchina (n = 1 nel caso di fig. 1) eI è il Fig. 2 – Caratteristica di magnetizzazione affetta da
saturazione e suo tratto non saturo (curva di traferro g).
fasore corrente di statore.
La condizione di non linearità del circuito magnetico principale (quello percorso dal flusso al traferro),
impone di determinare il flusso di polo  come effetto della f.m.m. risultante al traferroMe:
(4)
Me  Mc  M .
In effetti, per la non linearità della saturazione magnetica, non è lecito calcolare l’effetto risultante
come somma degli effetti dovuti alle singole f.m.m. (principio di sovrapposizione).
Indicato conu il flusso di polo utile sostenuto dalla f.m.m. risultanteMe, il corrispondente fasore
f.e.m. utileEu di fase, misurato legandolo al verso del flusso con la regola della vite destrorsa, vale:
E u   j N e  u
2 .
(5)
Macchina sincrona isotropa: note aggiuntive Oltre alla f.e.m.Eu dovuta al flusso utile, negli avvolgimenti di armatura è indotta anche una f.e.m.
dovuta al flusso dispersoEa; poiché i tubi di flusso di dispersione si sviluppano lungo tronchi
caratterizzati da notevole lunghezza in aria (dispersione in cava, attorno alle teste di matassa degli
avvolgimenti, dispersione fra le teste denti di statore) tale f.e.m.Ea si può ritenere proporzionale alla
causa che la genera, cioè alla corrente di statoreI, tramite il parametro reattanza di dispersione Xa:
E a   jX a  I .
(6)
2
Se la c.d.t. resistiva R I è trascurabile, la tensione di fase risulta quindi data da:
Vf  E u  E a  E u  jX a  I .
(7)
Considerando la (1) e la (3), dalla (4), relativa a fasori spaziali f.m.m. agenti al traferro, si può passare
alla seguente equazione fasoriale:
(8)
N c  Ie  N c  Ic  k M  I ,
oveIe =Me/Nc è la f.m.m. risultante al traferro, divisa per il N° spire di campo per polo Nc.
Dividendo la (8) per Nc si ottiene:
dove
Ie  Ic   P  I ,


P  k M Nc  3  2    Ne
 n  Nc 
,
(8)
(9)
detto coefficiente di Potier, consente di passare dal fasore corrente di faseI ad un fasore spaziale in
termini di corrente di eccitazione.
Mentre la fig. 1 illustra la teoria di Potier (determinazione della tensione di fase ai morsettiVf a
partire dalle f.m.m. agenti al traferro,Mc,M), è di solito necessario applicare la procedura opposta,
cioè determinare la corrente di eccitazione Ic necessaria a garantire una certa condizione di
funzionamento ai morsetti (tensione di fase V, corrente I, sfasamento relativo ): la corrispondente
procedura fasoriale è nota come costruzione di Potier, ed è rappresentata in fig. 3.
Dai fasoriVf eI, sfasati dell’angolo , positivo
come in figura (di ritardo della corrente rispetto
Eu j  X a  I
alla tensione: carico di tipo induttivo), in base
Vf
alla (7) si ottiene il fasore f.e.m. utile:
E u  Vf  jX a  I
(10)

I
Entrando con l’ampiezza Eu diEu nella curva di
Ie

fig. 2, si ottiene la ampiezza Ie del fasore
P  I
correnteIe (rappresentativo della f.m.m. Ic
risultante al traferroMe), da rappresentare in
Fig. 3 – Costruzione di Potier.
quadratura in anticipo rispetto aEu.
Noto il fasoreI = P I, rappresentativo della f.m.m. di reazioneM, dalla (8) si ottiene:
Ic  Ie  I  Ie   P  I ,
(11)
Oltre all’angolo  (sfasamento tra tensione e corrente, assunto positivo in senso antiorario, in caso di
carico con natura induttiva), in fig. 3 è evidenziato anche l’angolo  tra i fasoriIc eI = P I,
rappresentativi rispettivamente della f.m.m. di campo e di reazione.
2. Caratteristiche di funzionamento della macchina sincrona isotropa in saturazione
Le condizioni di funzionamento a regime della macchina sincrona isotropa sono completamente
definite dal valore delle seguenti 4 variabili di indotto e induttore: V, I, , Ic.
Macchina sincrona isotropa: note aggiuntive Dunque, fissando due variabili e rappresentando graficamente il legame tra le due rimanenti si
ottengono delle caratteristiche, che assumono nomi diversi in relazione al legame che indicano.
Alcune di queste curve sono determinabili sperimentalmente in modo agevole; questo consente la
identificazione dei parametri della macchina Xa e P a partire da opportune prove.
Va infine osservato che le caratteristiche che saranno prese in esame sono abbastanza simili a quelle
proprie delle macchine anisotrope, per cui le considerazioni fatte possono approssimativamente
adattarsi anche a tali macchine.
2.1. Caratteristiche di tensione
Sono dette caratteristiche di tensione le curve Vf - Ic per I e cos costanti.
Sotto questo aspetto anche la caratteristica di magnetizzazione è una caratteristica di tensione.
Di primario interesse sono le caratteristiche per I = cost (e, in particolare I = In) e cos = 0R e cos =
0A (dove R = ritardo e A = anticipo della corrente rispetto alla tensione di fase). Tali caratteristiche
sono strettamente legate alla curva a vuoto. Infatti da un qualsiasi punto della curva a vuoto, che
identifica la coppia di valori Eu - Ie della costruzione di Potier, si passa alla caratteristica di tensione a
carico a cos = 0R tramite una c.d.t. XaIn e un aumento di corrente di eccitazione pari a PIn (fig. 4):
in figura Ick è la corrente di campo che, in corto circuito trifase permanente fa circolare la corrente
nominale In di statore. Le costruzioni di Potier (1) e (2) giustificano il passaggio per cos = 0R e cos
= 0A rispettivamente; Vf è un valore generico.
Vf
Ick
Ie PIn
Ic
XaIn
XaIn
Vf
Ie
Ie
PIn
PIn
Ic
Ic
Fig. 4 – Derivazione delle caratteristiche a I = In e cos = 0A, 0R dalla caratteristica a vuoto.
3
Macchina sincrona isotropa: note aggiuntive Egualmente, la caratteristica di tensione a carico, a cos = 0A si ottiene applicando un aumento di
tensione XaIn e una riduzione della corrente di campo PIn.
In definitiva, con la traslazione dei triangoli ABC e AB'C' i punti C e C' tracciano le due
caratteristiche in studio. Per I = In e Vf = 0 (in corto circuito a I = In) la curva a cos = 0R taglia l’asse
delle ascisse per Ic = Ick. Nel punto dove la curva a cos = 0A taglia l’asse delle ordinate, ossia con Ic
= 0, la macchina funziona in autoeccitazione.
Il fatto che le caratteristiche di tensione a I = In e cos = 0 si ottengano per traslazione dalla curva a
vuoto, noti che siano Xa e P, non è di per sé di grande rilevanza, ma mostra che invece è possibile, in
linea di principio, il procedimento opposto (Fig. 5).
Vf
A
O
XaIn
B
C
PIn
A
O
B
Ick
OC = OC
C
Ic
XaIn= Eu
Ie PIn
IIckck
Fig. 5 – Determinazione grafica di XaIn e di PIn; il triangolo OAC è detto triangolo di Potier.
Misurate cioè sperimentalmente queste curve, sarà possibile determinare i parametri interni della
macchina Xa e P. A questo scopo si osservi il punto di funzionamento in corto circuito a I = In,
riportandovi il triangolo ABC di fig. 4. Il triangolo OAC che in questo modo è stato messo in evidenza
può essere interpretato come una costruzione di Potier (con origine in B) per le condizioni di corto
circuito. Infatti AB = Eu =XaIn; OB = Ie ; BC = PIn e infine OC = Ic; Vf naturalmente è nulla.
Di questo triangolo, che è chiamato triangolo di Potier, le misure forniscono la base OC e l'angolo
CÔA. Se questi due elementi vengono applicati, sempre tramite traslazione, ad un generico punto della
caratteristica a cos = 0R, C situato in una zona dove la saturazione sia sensibile la semiretta uscente
da O' con angolo pari a CÔA sull'orizzontale ha un'intersezione ben definita con la curva a vuoto in un
punto A', che così identifica l'altezza incognita A'B' = XaIn, ed il segmento incognito B'C' = PIn da
cui, nota In, si desumono Xa ed P. In linea di principio, un'analoga costruzione potrebbe essere
tracciata servendosi della curva corrispondente a cos = 0A e I = In.
Il procedimento ora descritto non è nella pratica utilizzato integralmente come descritto, in quanto la
determinazione sperimentale delle curve a cos = 0 e I = In richiede di collegare la macchina a un
carico trifase in grado di far circolare la corrente nominale, anche se solo di natura reattiva: questa
4
Macchina sincrona isotropa: note aggiuntive operazione è infatti piuttosto onerosa, specie in caso di prove con macchine di grande taglia. In pratica
si procede mediante l'uso combinato di tre diversi rilievi sperimentali, come si vedrà nel seguito.
Altre caratteristiche ad I = cost e cos  0 assumono l'andamento indicato in fig. 6 ma sono di scarso
interesse pratico; lo stesso si può dire per le caratteristiche di tensione su impedenza costante.
Vf
5
Ic
Fig. 6 – Caratteristiche di tensione a I = In e cos = 0, 0.8R, 1.
2.2. Caratteristiche di corrente
Le curve che esprimono la relazione I = I(Ic) sono denominate caratteristiche di corrente.
Come parametro è assunto normalmente Vf = cost (ed in particolare Vf = Vfn) e cos = cost o in
alternativa P = cost; a questa alternativa corrispondono due distinte famiglie di curve:
 le curve a cos = cost sono dette caratteristiche di regolazione e rivestono scarso interesse pratico;
 le curve a potenza attiva costante hanno invece grande importanza e per la loro forma sono
denominate curve a V.
Le condizioni Vf = cost e P = cost sono realizzabili in pratica senza difficoltà collegando la macchina
sincrona ad una rete a potenza infinita, e quindi a tensione costante indipendentemente dalla potenza
scambiata con la macchina sincrona; inoltre la potenza meccanica entrante nella macchina, e quindi la
potenza attiva uscente, è mantenuta costante fissando la coppia del motore primo (ad esempio con
portata di fluido costante, se il motore primo è una turbina). Le variazioni della corrente di eccitazione
influiscono allora solo sulla potenza reattiva, e quindi sulla corrente di indotto.
La più importante delle curve a V, che hanno nel loro complesso l'andamento indicato in fig. 7 è quella
a potenza attiva nulla, che può essere rilevata sperimentalmente, una volta connessa la macchina alla
rete, senza alcuna spesa di potenza meccanica.
Vf = Vfn
Ic0n
Ic
Fig. 7 – Curve a V e caratteristiche di regolazione a cos = cost, tracciate per Vf = Vfn.
Macchina sincrona isotropa: note aggiuntive Naturalmente i punti più bassi delle curve a V corrispondono al funzionamento a cos = 1, e unendoli
è identificata la caratteristica di regolazione a tensione costante e cos = 1; le caratteristiche a Vf =
cost e cos = cost < 1 in anticipo e in ritardo sono indicate a tratteggio nella medesima figura: è ovvio
che la curva a V per P = 0 e quella di regolazione a cos = 0 coincidono.
Mediante le curve a V è possibile individuare nel piano I – Ic la zona in cui è possibile un reale
funzionamento della macchina (Fig. 8). Essa è determinata dai seguenti limiti:
1) inferiormente: la curva a V per P = 0 (nei due tratti a cos = A e cos = R);
2) a destra: la retta verticale di massima corrente di eccitazione IcMAX;
3) sopra: la retta orizzontale di massima corrente di indotto In;
4) sempre sopra: la curva a V per potenza attiva massima PMAX, ossia per la massima potenza
meccanica che il motore primo può fornire; infatti se la macchina funziona da generatore sarà
sempre chiamata a fornire anche potenza reattiva, per cui la potenza meccanica massima del
motore primo è inferiore alla potenza apparente massima per cui è dimensionato l'indotto (questa
limitazione non sussiste se la macchina funziona come motore);
5) la zona (A) in alto a sinistra, anche se possibile in via teorica, corrisponde a condizioni instabili.
cos = 0A
cos = 0R
IcMAX
Ic
Fig. 8 – Limiti di funzionamento di una macchina sincrona identificati sul piano I – Ic.
La zona indicata con (A) può corrispondere a funzionamento instabile.
2.3. Fattore di potenza nominale e potenza nominale
Fino ad ora la potenza nominale di una macchina sincrona non è stata definita in modo esauriente.
Per quanto riguarda l'indotto, il suo funzionamento è del tutto simile a quello del trasformatore, con
perdite nel ferro proporzionali al quadrato della f.e.m. (e, in prima approssimazione della tensione) e
perdite nel rame proporzionali al quadrato della corrente.
Di conseguenza la potenza nominale dell'indotto, limitata solo da questioni termiche, è una potenza
apparente e va espressa in [VA]. Però, a potenza apparente di indotto costante, la corrente di campo (e
quindi la perdita di rotore) è tanto maggiore quanto più basso è il fattore di potenza.
Di conseguenza va precisata in modo diretto o indiretto la massima corrente di eccitazione
ammissibile. Se si osserva il punto C di fig. 8, questo corrisponde ad una corrente di indotto massima
(e quindi potenza apparente massima) e, simultaneamente alla massima corrente di eccitazione. Per il
punto C passerà la curva a cos = cost corrispondente al fattore di potenza nominale della macchina
cosn , che va inteso come il minimo valore del fattore di potenza a cui la macchina può funzionare a
potenza apparente nominale An senza eccedere i limiti termici del rotore.
Quindi il cosn va interpretato nel senso che per cos compreso tra 1 e cosn la macchina può erogare
la potenza nominale An senza superare la Ic massima, quindi senza sovraccaricare termicamente il
rotore; per cos < cosn la macchina dovrà funzionare con I < In (e quindi con A < An) per non
superare la IcMAX : dunque, sarà costretta a erogare una potenza apparente inferiore.
In pratica il fattore di potenza nominale è generalmente compreso tra 0.95 e 0.8.
6
Macchina sincrona isotropa: note aggiuntive 2.4. Determinazione di P e Xa tramite la curva a V a potenza attiva nulla
A partire dalla curva a vuoto Vfo(Ic), dalla caratteristica di corto circuito permanente Ik(Ic) e dalla curva
a V a P = 0 è possibile determinare i parametri Xa e P. L'interesse nell’uso di queste tre curve risiede
nel fatto che tutte possono essere rilevate sperimentalmente senza dispendio di potenza attiva, e
quindi in modo pratico ed economico.
La determinazione di Xa ed P si riallaccia alla costruzione descritta nel Parag. 2.1.: a tal fine, si
riportano le tre suddette caratteristiche in un unico diagramma, con in comune la scala delle correnti di
campo (Fig. 9, a destra); si procede quindi come descritto nel seguito:
 dalla curva in corto circuito permanente Ik(Ic), entrando con I = In si ottiene il punto Ick;
 si osservi che dal punto Ick parte la caratteristica di tensione a I = In, cos = 0R, di cui una porzione
è tratteggiata in fig. 9 a destra: tuttavia, come detto in precedenza, si suppone qui di non disporre di
tale caratteristica, perché di rilievo sperimentale oneroso (richiede un carico a corrente nominale);
 Ick rappresenta il funzionamento in corto circuito a I = In sul piano delle caratteristiche di tensione,
ossia la base del triangolo di Potier (come mostrato nel diagramma di fig. 9 a sinistra);
 ancora in corrispondenza di I = In si determina sulla curva a V per P = 0 (ramo a cos = 0R) il
punto A, cui corrisponde una condizione di funzionamento con Vf = Vfn (Vf infatti rimane fissa
lungo tale curva a V): al punto di funzionamento A corrisponde una corrente di campo IcA;
 lungo la già citata (ma non disponibile) caratteristica di tensione a I = In e cos = 0R, il punto A si
traduce in C', di coordinate Vfn e IcA;
 da questo punto in poi si procede esattamente come indicato in Parag. 2.1, fig. 5 (riprodotta a
sinistra in fig.9): si riporta, a partire da C' verso sinistra, la base O'C' = Ick del triangolo di Potier;
 tracciando per O' la retta O'A' avente la inclinazione del tratto non saturo della caratteristica a
vuoto, l'intersezione di tale retta con la caratteristica a vuoto determina il punto A';
 i punti A', O' e C' costituiscono i vertici del triangolo di Potier, per cui si ha: A'B' = XaIn e B'C'
= PIn , da cui la identificazione dei parametri Xa ed P.
Vf0 Ik
Ik
A
Vfn
In
O
Vf0
C
O B
Ic0n Ick
IcA
Ic Ic
Fig. 9 – Determinazione di Xa e P a partire dalla curva a vuoto Vfo(Ic), dalla caratteristica di corto
circuito Ik(Ic) e dalla curva a V a P = 0. Il punto C' (cfr. fig. 5, riprodotta a sinistra) appartiene alla
caratteristica di tensione per I = In, cos = 0R. Individuato il punto A', si prosegue come in fig. 5.
2.5 Alcune situazioni tipiche, analizzate con la costruzione di Potier
Si osservino le cinque costruzioni di Potier di fig. 10, tutte con Vf = cost, I = cost e cos = 0A, 0.7A,
1, 0.7R, 0R. Ricordando che la direzione della I coincide con l'asse di reazione e quella della Ic con
l'asse di induttore risulta che:
 cos = 0R (fig. 10.1): f.m.m. di campo e di reazione antagoniste  potenza attiva nulla; reazione
di indotto puramente smagnetizzante (cfr. fig. 11.b): in tali condizioni l'angolo tra l'AI (ortogonale
alla Ic) eVf è nullo;
7
Macchina sincrona isotropa: note aggiuntive  cos = 0A (fig. 10.2): f.m.m. di campo e di reazione equidirette:  potenza attiva nulla; reazione
di indotto puramente magnetizzante (cfr. fig. 11 c);
 cos = 1 (fig. 10.3): la macchina eroga potenza attiva (e potenza reattiva nulla)  la reazione di
d’indotto è solo torcente, con coppia elettromagnetica frenante (cfr. fig. 11.a, che mostra la ruota
polare reale di induttore e quella fittizia di armatura, dovuta al campo rotante; cfr. anche fig. 11.a’ e
fig. 12 s); l'angolo tra l’asse interpolare (AI) eVf è diverso da 0;
 cos = 0.7R, 0.7A (fig. 10.4, 5): la macchina eroga sia potenza attiva che potenza reattiva 
l'angolo tra AI eVf è diverso da 0 (cfr. fig. 12 c,d).
Quindi per cos = 0 la reazione di indotto è sempre diretta lungo l'asse polare: il suo effetto è detto
longitudinale o diretto. Per cos  0, ossia con potenza attiva erogata, l'angolo tra l'asse interpolare ed
il fasore tensione è sempre diverso da zero, ed è quindi indice di conversione elettromeccanica di
potenza. Quest'angolo, indicato con , è detto angolo di carico. Infine con   0 la f.m.m. utileMe ha
direzione diversa da quella di eccitazioneMc, ossia il carico meccanico provoca un effetto torcente.
XaI
Vf X I
a
Vf
Ie
PI
I
I
Ic
XaI
Ie PI
Ic
XaI
Vf
Vf
I
PI
Ic
PI
Ic
Ie
Ie
XaI
Vf
I
PI
Ic
Ie
Fig. 10 – Costruzioni di Potier per diversi valori di cos e identificazione dell’angolo di carico .
8
Macchina sincrona isotropa: note aggiuntive 9
Fig. 11 – Schematizzazione di situazioni di funzionamento di una macchina sincrona: rotore con ruota
polare reale; statore con ruota polare fittizia, dovuta al campo rotante delle correnti trifase. a) = a’)
reazione puramente torcente; b) reazione smagnetizzante; c) reazione magnetizzante.
s
c
d
Fig. 12 – Funzionamento con cos = 1 (sinistra), cos = 0.7R (centro), cos = 0.7A (destra).
3. La costruzione di Behn-Eshemburg
La costruzione di Potier interpreta i fenomeni che hanno sede in una macchina sincrona isotropa in
modo soddisfacente, ma relativamente complesso; essa comprende infatti ben due somme fasoriali
(Vf + jXa I ) e (Ie  P I ) e un passaggio non lineare (Eu Ie ). Se si ammette di trascurare la
saturazione, e cioè il legame non lineare (Eu Ic ), il procedimento può essere molto semplificato, e
il funzionamento della macchina è rappresentato da una sola equazione fasoriale.
La costruzione semplificata che così si ottiene è detta di Behn-Eshemburg, o dell'unica reattanza.
Data l’ipotesi di linearità, ad ogni singola causa si può far corrispondere un distinto effetto; inoltre, la
somma degli effetti dovuti a ciascuna delle cause agenti separatamente è uguale all’effetto dovuto alla
somma delle cause. Dunque, valgono le seguenti relazioni di proporzionalità:
Eu/Ie = E/(PI) = Ea/I = Eo/Ic




dove
Eu è la f.e.m. utile, dovuta alla f.m.m. risultante al traferro, corrispondente a Ie;
E è la f.e.m. dovuta alla reazione di armatura: per la ipotesi di linearità, si può porre: E = XI;
Ea è la f.e.m. dovuta ai flussi di dispersione di armatura: Ea = XaI;
Eo è la f.e.m. a vuoto, dovuta alla sola f.m.m. di campo, corrispondente a Ic; Eo è detta anche f.e.m.
interna della macchina sincrona.
Tracciando la costruzione di Potier in base ai rapporti di proporzionalità sopra riportati, si ha il
diagramma fasoriale di fig. 13: si osservi che, in base alla legge della induzione elettromagnetica
scritta con la formulazioneE = j, ciascun contributo di f.e.m. è in quadratura () in ritardo
Macchina sincrona isotropa: note aggiuntive rispetto al fasore corrente rappresentativo della f.m.m. cui ogni fasore contributo di f.e.m. è
proporzionale:Eu Ie;E  P I; Ea I;Eo Ic. In base alla considerazione cheEo Ic,
poichéIc è orientato secondo l’asse d (ovvero secondo l’AP), il fasore f.e.m. interna a vuotoEo è
orientato secondo l’asse q (ovvero secondo l’AI); dunque, come già osservato in precedenza, l’angolo
formato traEo eVf è l’angolo di carico . Inoltre, le due f.e.m. di ampiezza Ea = XaI e E = XI,
entrambe proporzionali alla corrente di armatura, possono essere sommate, definendo una unica c.d.t.
reattiva Vx = (Xa+X)I = XI, dove X = Xa+X è la reattanza sincrona.
E = XI
Ea = XaI
Vf
Ie
PI
Ie Ic
Ic
Ic
Fig. 13 – Derivazione della costruzione di Behn-Eshemburg dalla costruzione di Potier.
Vale dunque il diagramma fasoriale di fig. 14, noto come costruzione di Behn-Eshemburg, cui
corrisponde il circuito equivalente rappresentato a lato (in entrambi si è trascurata la c.d.t. RI).
jXI
X
Re
Eo
Vf
Eo
I
Vf

  I
 Ic Fig. 14 – Diagramma fasoriale di Behn-Eshemburg della macchina sincrona isotropa e relativo
circuito equivalente monofase (ipotesi di caduta resistiva trascurabile).
10
Macchina sincrona isotropa: note aggiuntive Nel diagramma fasoriale di fig. 14 sono evidenziati i seguenti angoli:
 angolo  di sfasamento del fasore correnteI rispetto al fasore tensione di faseVf;
 angolo di carico  tra il fasore tensione di faseVf e il fasore f.e.m. internaEo;
 angolo di reazione  tra il fasore correnteI e il fasore f.e.m. internaEo;
 angolo  tra i fasori corrente di indottoI e di campoIc, cioè tra le f.m.m. di armatura e di campo.
Tra tali angoli sussistono i seguenti legami:
=+;
 =  + /2 .
4. Energetica di una macchina sincrona isotropa connessa ad una rete a tensione costante.
In base al circuito equivalente di fig. 14, la potenza apparente complessa ai morsetti della macchina si
può esprimere come segue:
A = P + jQ = 3 Vf  I = 3 Vf  [(Eo Vf )/(jX)] = j3Vf  (Eo Vf )/X .
Considerando poi che, in base al diagramma fasoriale di fig. 14, con il riferimento adottato si ha:
Vf = Vf ;
Eo = Eoexp(j) ,
si ottengono le seguenti espressioni della potenza attiva e reattiva:
P = 3(Vf Eo/X)sin() ,
Q = 3Vf (Eocos()  Vf)/X .
Se si ipotizza che la macchina funzioni in parallelo rispetto ad una rete a tensione Vf costante, valgono
le seguenti osservazioni:
 l’espressione della potenza attiva P mostra che se l’angolo di carico  cambia segno (cioè se il
fasoreEo si sposta in ritardo rispetto aVf) anche la potenza attiva P, misurata come erogata,
cambia segno: dunque la macchina passa da funzionamento come generatore a funzionamento
come motore sincrono (questa reversibilità può effettivamente verificarsi, ad esempio nelle centrali
idroelettriche di generazione e pompaggio, con sistemi turbina-pompa, cfr. centrale di Edolo);
 in caso di funzionamento senza scambio di potenza attiva con la rete ( = 0), la macchina scambia
potenza reattiva Q: in caso di sovra-eccitazione (Eo > Vf), la potenza reattiva Q è erogata dalla
macchina, che si comporta dunque come un condensatore; in caso di sotto-eccitazione (Eo < Vf), la
macchina assorbe potenza reattiva dalla rete e quindi si comporta come un induttore: le macchine
sincrone usate per il solo scambio di potenza reattiva sono principalmente usate per il rifasamento
nei nodi delle reti di trasmissione dell'energia, e in tal caso sono chiamate compensatori sincroni.
5. Diagramma polare della macchina sincrona isotropa; curve di capability.
Il diagramma fasoriale di fig. 14, che corrisponde alle ipotesi di linearità della costruzione di BehnEshemburg, si presta, opportunamente trasformato, a dare origine ad un diagramma polare della
macchina sincrona isotropa, relativo alle correnti di induttore e di indotto.
La trasformazione consiste nel dividere le ampiezze Vfn, Eo e XI dei fasori di fig. 14 per la reattanza
sincrona X, osservando poi che alle quantità Vfn/X e Eo/X si possono rispettivamente far corrispondere
i valori Ic0n e Ic della corrente di campo. Ne consegue, dunque, il diagramma di fig. 15, in cui IA =
Icos e IR = Isin sono rispettivamente le componenti attiva e reattiva della corrente di statore: tali
fasori, moltiplicati per 3Vfn rappresentano anche la potenza attiva P e la potenza reattiva Q. Infine, dal
diagramma di fig. 15 si ottiene il diagramma polare di fig. 16.
Ogni punto S del piano di fig. 16 identifica la corrente di indotto OS, l'angolo , la corrente di campo
O'S (per la sua proporzionalità con Eo/X) e l'angolo . Valgono le seguenti proprietà:
 sull'asse reale, tramite un cambiamento di scala di fattore 3Vfn, si leggono le potenze attive;
 egualmente sull’asse immaginario si leggono le potenze reattive;
 nel semipiano superiore la macchina funziona da generatore ( > 0), mentre in quello inferiore da
motore ( < 0);
11
Macchina sincrona isotropa: note aggiuntive  nel semipiano di destra vi è potenza reattiva erogata (sovra-eccitazione), nel semipiano di sinistra
assorbita (sotto-eccitazione).
 il segmento OO' è pari a Ic0n , corrente di campo che a vuoto corrisponde alla tensione nominale
(sulla caratteristica non satura);
 le circonferenze di centro O sono luoghi con corrente di indotto (o potenza apparente) costante;
 le circonferenze di centro O’ sono luoghi con corrente di eccitazione costante.
12
IR
Eo/X  Ic
IA
Vfn/X  Ic0n
Fig. 15 – Diagramma fasoriale derivato da quello della costruzione di Behn-Eshemburg di fig. 14,
attraverso la divisione per X dei fasori di ampiezza Vfn, Eo e XI.
P
Ic_max
Ic

S
Q
Ic0n
Fig. 16 – Diagramma polare della macchina sincrona isotropa e zone di funzionamento possibile; le
curve limite a tratteggio sono denominate curve di capability. Punti salienti: punto C: massima potenza
apparente e minimo fattore di potenza: cosn; punto D: funzionamento come compensatore sincrono
alla massima potenza reattiva erogata consentita dall'eccitazione.
Macchina sincrona isotropa: note aggiuntive Il diagramma polare di fig. 16 si presta assai bene a visualizzare i limiti di funzionamento della
macchina, in modo più rappresentativo di quanto visto dalle curve a V.
I luoghi dei limiti di funzionamento, detti anche curve di capability, sono:
 circonferenza con centro O e raggio In: massima corrente di indotto (massima potenza apparente);
 circonferenza con centro O’ e raggio Icmax: massima corrente di campo;
 retta orizzontale di ordinata Pmax: massima potenza meccanica fornita dal motore primo (solo nel
funzionamento come generatore);
 retta verticale per O’: angolo lim limite di stabilità statica, pari a 90°.
 punto C: funzionamento a In e Icmax: identifica il valore di cosn.
6. Coppia elettromagnetica della macchina sincrona isotropa; studio della stabilità.
Se si trascurano le perdite della macchina sincrona rispetto alla potenza attiva ai morsetti (ipotesi
ragionevole per le macchine di taglia medio-grande, con  > 0.95), la potenza attiva P può ritenersi
all’incirca uguale a quella meccanica all’albero Pm: Pm = P + Pp  P. Esprimendo poi tale potenza
come Pm = Ceo, dove o= /n è la velocità di rotazione in sincronismo a regime, per la coppia
elettromagnetica Ce si ha:
Ce = 3[(Vf Eo)/(oX)]sin() .
Osservando questa espressione, valgono le seguenti considerazioni:
 l’angolo  risulta positivo se la macchina eroga potenza elettrica (alternatore), negativo se la
macchina assorbe potenza elettrica (motore);
 a parità di coppia, Eo (e dunque la corrente di eccitazione) e sin() (assimilabile a  per angoli
piccoli) variano in modo inversamente proporzionale;
 nel funzionamento a regime stazionario in parallelo ad una rete di potenza infinita, le quantità Vf, X
e o possono essere considerate costanti;
 la coppia elettromagnetica massima CeM si ottiene per  = 90° e vale evidentemente:
CeM = 3[(Vf Eo)/(oX)] ;
 in linearità magnetica, la coppia CeM è proporzionale alla corrente di campo Ic (in quanto Eo  Ic).
6.1. Stabilità statica
Poiché la caratteristica meccanica di una macchina sincrona (nel piano Ce - ) è rappresentato da un
segmento verticale passante per  = o, per valutare gli effetti della variazione di carico è necessario
considerare la cosiddetta caratteristica pseudo-meccanica Ce(), mostrata in fig. 17.
Ce
Ce
CeB
CeA
A B
Fig. 17 – Sinistra: caratteristica Ce- (pseudo-meccanica); destra: analisi di stabilità statica come
generatore: il punto A è di funzionamento stabile, perché ad un aumento di angolo di carico
corrisponde un aumento di coppia elettromagnetica; il punto A’, invece, si trova in zona instabile.
13
Macchina sincrona isotropa: note aggiuntive Si supponga che la macchina funzioni come generatore in una condizione di carico rappresentata dal
punto A, con coppia CeA e angolo di carico A: in tale situazione di regime, la coppia motrice CmA del
motore primo e quella elettromagnetica resistente CeA che si sviluppa nella macchina sono uguali fra
loro (trascurando le perdite meccaniche). Si consideri ora la seguente sequenza di operazioni:
 si supponga di applicare un lento e graduale aumento della coppia motrice Cm del motore primo,
dal valore CmA al valore CmB > CmA (nel caso di una turbina tale aumento consegue all’incremento
di portata del fluido di lavoro);
 venendo a mancare l’equilibrio delle coppie all’albero, con la nascita di una coppia accelerante, il
rotore tende a spostarsi in avanti, nello stesso senso di rotazione della macchina;
 conseguentemente anche l’angolo di carico  aumenta (cfr. fig. 14); questo fa aumentare la coppia
elettromagnetica frenante, fino al raggiungimento di un nuovo equilibrio in corrispondenza
all’angolo di carico B , per il quale risulta di nuovo CeB = CmB;
 in questo nuovo assetto, di tipo stabile, si ha un aumento della potenza attiva erogata verso la rete.
Se il medesimo procedimento si effettuasse a partire dal punto A’, l'aumento di  implicherebbe una
diminuzione della coppia elettromagnetica: non sarebbe dunque più possibile il raggiungimento di una
nuova condizione di equilibrio tra coppia motrice e resistente e la macchina, sotto l’azione della
coppia accelerante, perderebbe il sincronismo con la rete (perdita di passo), andando in velocità di
fuga: questo evento va evitato, perché accompagnato da violente coppie alternativamente, con
conseguenti gravi danni al rotore, al giunto dell’albero ed al motore primo.
Analoghe considerazioni valgono per il funzionamento da motore: in questo caso, una maggiore
richiesta di coppia meccanica all’albero implica ancora un aumento (in modulo) dell’angolo di carico
, con il raggiungimento di nuove condizioni di equilibrio, purché la macchina sia in grado di produrre
una coppia elettromagnetica più elevata (in questo caso motrice): se ciò non può verificarsi, la perdita
di passo, ancora accompagnata da forti coppie alternative, si conclude con l’arresto della macchina.
In linea di principio la tendenza al verificarsi della perdita del passo potrebbe essere contrastata
aumentando bruscamente (forzando) la corrente di eccitazione, con un conseguente aumento di CeM ed
una riduzione di : a causa però della grande costante di tempo del circuito di campo, è difficile che il
regolatore che governa la corrente di eccitazione possa intervenire in tempo utile.
Per questa ragione tutte le considerazioni sulla stabilità vengono fatte a Ic = costante.
Quanto è stato finora detto riguardo alla stabilità prescinde dal fatto che lo spostamento da un angolo
di carico ad un'altro è accompagnato da un transitorio elettromeccanico, durante il quale le variazioni
di  potrebbero raggiungere zone di instabilità. Per tale ragione le considerazioni finora fatte
riguardano la cosiddetta stabilità statica, in cui si assume che il carico, e quindi , vari con incrementi
infinitesimi e i transitori elettromeccanici siano trascurabili; l'angolo  = 90°, che separa la zona stabile
dalla zona instabile è perciò detto angolo limite di stabilità statica.
6.2. Oscillazioni pendolari
Di una macchina sincrona connessa in parallelo è importante conoscere il comportamento in
conseguenza di una brusca variazione della coppia meccanica motrice (funzionamento come
generatore) o frenante (funzionamento come motore) applicate all'asse. Si è visto che in una macchina
sincrona collegata in parallelo alla rete ad ogni valore della coppia applicata corrisponde un dato
valore dell'angolo  tra il fasoreEo e il fasoreVf. Se la coppia applicata varia bruscamente, per
effetto dell'inerzia delle masse rotanti il valore di , corrispondente alle nuove condizioni di carico,
non viene raggiunto istantaneamente ma dopo un certo intervallo di tempo; inoltre, il cambiamento
dell’angolo di carico  è accompagnato da una serie di oscillazioni di carattere pendolare.
Supponendo che la macchina funzioni da generatore (Eo in anticipo rispetto aVf,  > 0, cfr. fig. 14) e
che la coppia motrice subisca una brusca diminuzione per cui si passa dalla condizione iniziale di
carico caratterizzata da un angolo 1 a quella finale caratterizzata dall'angolo 2 < 1 (Fig. 18), il
fenomeno può essere spiegato qualitativamente nel modo seguente:
14
Macchina sincrona isotropa: note aggiuntive  negli istanti immediatamente successivi alla brusca diminuzione della coppia motrice applicata,
finché si verifica che  > 2 la coppia elettromagnetica frenante è maggiore della coppia motrice,
con conseguente riduzione della velocità del rotore e decremento di energia cinetica in esso
accumulata;
 raggiunta la posizione  = 2, la differenza tra coppia frenante e motrice si annulla, ma il rotore per
effetto dell'inerzia continua a ruotare con velocità meno elevata di quella di sincronismo;
 oltrepassata la posizione  = 2, con  in diminuzione, la coppia elettromagnetica frenante diviene
inferiore rispetto alla coppia motrice, per cui la velocità inizia ad aumentare fino a raggiungere la
velocità di sincronismo in corrispondenza di un valore limite ', con ' < 2;
 raggiunta la posizione  = ', la velocità del rotore continua ad aumentare, diventando maggiore di
quella di sincronismo e  riprende ad aumentare fino a raggiungere nuovamente la posizione  = 2
e ad oltrepassarla;
 il rotore finisce per raggiungere la posizione finale di equilibrio  = 2 attraverso una serie di
oscillazioni pendolari attorno a tale posizione, più o meno smorzate a seconda dell'entità dei
fenomeni dissipativi di energia.
Vf
Fig. 18 – Condizioni di regime iniziale ( = 1) e finale ( = 2) di un generatore sincrono in parallelo
alla rete, soggetto a una brusca diminuzione di coppia motrice applicata (a tratteggio sono mostrate le
posizioni pendolari transitorie intermedie della f.e.m.Eo).
Lo smorzamento delle pendolazioni è usualmente affidato alla gabbia smorzatrice: si tratta di un
avvolgimento distribuito costituito da barre in materiale conduttore, disposte sul rotore verso il
traferro; tali barre sono fra loro collegate da anelli di corto circuito disposti su entrambe le fronti del
pacco lamiere. Nel caso di macchine sincrone isotrope, le barre sono alloggiate, verso il traferro, nelle
stesse cave dell’avvolgimento di campo (fig. 19 a sinistra), mentre nelle macchine a poli salienti le
barre sono inserite in apposite cave ricavate lungo le espansioni polari (fig. 19 a destra).
Fig. 19 – Collocazione delle barre della gabbia smorzatrice (a sezione circolare: ), poste lungo la
periferia del circuito magnetico di rotore. A sinistra: macchina sincrona isotropa a 2 poli:
alloggiamento, verso il traferro, nelle cave dell’avvolgimento di campo; a destra: macchina sincrona a
poli salienti a 6 poli: alloggiamento in apposite cave ricavate nelle espansioni polari.
15
Macchina sincrona isotropa: note aggiuntive Il principio sul quale si basa l’azione smorzante della gabbia smorzatrice è il seguente:
 quando la macchina funziona a regime, il rotore è perfettamente sincrono con il campo rotante al
traferro, le barre della gabbia vedono un campo magnetico stazionario, e dunque nessuna f.e.m.
viene indotta in tali barre, ne vi possono circolare correnti: è come se la gabbia fosse assente;
 quando si verifica una variazione dell’angolo di carico , la velocità istantanea del rotore  è
diversa da quella del campo al traferro o, il flusso concatenato con la gabbia varia nel tempo, con
nascita di f.e.m. nelle barre, e circolazione di correnti: per la legge di Lenz, tali correnti tendono ad
opporsi alla causa che le ha generate, ovvero producono una azione antagonista proporzionale alla
velocità differenziale   o: a seconda del segno della differenza   o, tale azione risulta
frenante o accelerante;
 in termini energetici si può dire che le pendolazioni si smorzano perché le corrispondenti variazioni
di energia cinetica vengono progressivamente perse, per effetto Joule, nella gabbia.
La coppia di smorzamento Cs sviluppata dalla gabbia si può dunque esprimere come:
Cs = ks(  o) .
In generale, lo studio delle oscillazioni pendolari richiede l'integrazione numerica del sistema di
equazioni differenziali non lineari che descrive il comportamento elettromeccanico della macchina.
Tale studio può tuttavia essere semplificato e ricondotto alla soluzione di un'unica equazione
differenziale lineare del secondo ordine sulla base delle seguente ipotesi:
 macchina non satura con resistenza di indotto e perdite nel ferro trascurabili;
 evoluzione elettrica lentamente variabile, ovvero comportamento elettrico quasi stazionario: è
dunque lecito l’uso dell’espressione della coppia elettromagnetica ricavata per il funzionamento di
regime: Ce = 3[(Vf  Eo)/(oX)]sin();
 piccola ampiezza delle oscillazioni dell'angolo  e della velocità angolare  nell'intorno di un
punto di equilibrio.
Per un generatore sincrono, si consideri un punto di funzionamento a regime permanente stabile,
corrispondente a un valore 1 dell'angolo di carico. Per tale punto vale la relazione:
Cm1 = Ce1 ,
dove Cm1 è la coppia motrice del motore primo (ad esempio, una turbina), Ce1 è la coppia
elettromagnetica del generatore corrispondente all’angolo di carico 1:
Ce1 = 3[(Vf Eo)/(oX)]sin(1)
.
La pulsazione o in condizioni di sincronismo vale: o = on.
Quando la velocità della macchina varia con conseguente uscita transitoria dal sincronismo,
l'equazione del moto del gruppo rotante (motore primo + generatore) è data da:
Cm  Ce  Cs = Jd/dt ,
con J momento d'inerzia complessivo (generatore + motore primo, visto all’albero del generatore).
Analizzando il comportamento della macchina per piccole variazioni nell'intorno del punto di
equilibrio (Ce1-1), è possibile linearizzare questa equazione nell'intorno di tale punto.
In tal caso, espressa come:
Cm = Cm1 + Cm~
la coppia motrice (con Cm~ piccola variazione intorno a Cm1), ad essa corrispondono un angolo di
carico e quindi una velocità e una coppia elettromagnetica esprimibili rispettivamente come:
 = 1 + ~
 = o + ~
Ce = Ce1 + Ce~ .
L’equazione differenziale diviene allora:
(Cm1 + Cm~)  (Ce1 + Ce~)  ks[(o + ~)  o] = Jd(o + ~)/dt ,
da cui, considerando che Cm1 = Ce1 , segue la seguente equazione alle piccole oscillazioni:
16
Macchina sincrona isotropa: note aggiuntive Cm~  Ce~  ks~ = Jd~/dt .
A questo punto è necessario esprimere la variazione di velocità ~ e la variazione di coppia
elettromagnetica Ce~ in funzione della variazione dell'angolo di carico ~ .
Indicato con n il numero di paia poli, per la variazione di velocità risulta:
~ = (1/n)d~/dt .
Espressa la coppia elettromagnetica frenante prodotta dal generatore mediante uno sviluppo in serie di
Taylor nell'intorno di 1 si ottiene, trascurando i termini dello sviluppo successivi ai primi due:
Ce() = Ce(1 + ~)  Ce(1) + ~(dCe/d)( = 1) = Ce1 + Ce~ ,
con
Ce~ = 3[(Vf Eo)/(oX)]cos(1)~ = 3n[(Vf Eo)/(oX)]cos(1)~ = kCe1~ .
Il coefficiente kCe1 corrisponde alla pendenza nel punto 1 della curva coppia-angolo di carico Ce();
esso è analogo a una costante di elasticità, esprimendo proporzionalità tra variazione ~ di  e
variazione Ce~ della coppia Ce, e viene comunemente chiamato coppia sincronizzante.
Dunque, sostituendo le ultime espressioni di ~ e di Ce~ nella equazione differenziale alle variazioni, e
moltiplicando ogni termine per n/J si ottiene:
d2~/dt2 + (ks/J)d~/dt + kCe1(n/J)~ = (n/J)Cm~ .
Quest’ultima è un'equazione differenziale lineare del secondo ordine nell'incognita ~: la sua soluzione
fornisce l'andamento nel tempo della variazione dell'angolo di carico a fronte di una variazione della
coppia motrice esterna. Introducendo le seguenti quantità:
p = (kCe1n/J)1/2 = pulsazione propria, non smorzata;
 = ks/[2(kCe1nJ)1/2] = coefficiente di smorzamento,
l’equazione diventa infine:
d2~/dt2 + 2pd~/dt + p2~ = (n/J)Cm~ .
Con <1 (ossia se l'effetto smorzante è piccolo rispetto all'effetto sincronizzante, come di fatto avviene
nelle macchine), la soluzione è del tipo oscillatorio smorzato:
~(t) = Dexp(t/s)sin(st  ) +  ,




dove :
2 1/2
s è la pulsazione in presenza di smorzamento:
s = p (1 ) ;
s è la costante di tempo, pari a: s = 1/(p) ;
D e  sono costanti di integrazione, da determinare in base alle condizioni iniziali;
 = 2  1 è la variazione dell’angolo di carico a transitorio esaurito, dove 2 è l’angolo di carico a
regime imposto dalla coppia motrice Cm2, soluzione della equazione:
Cm2 = 3[(Vf Eo)/(oX)]sin(2)
.
Dalla soluzione formulata si può determinare la espressione della derivata:
d~(t)/dt = Dexp(t/s)[cos(st  )s  sin(st  )/s] .
Infine, imponendo le condizioni iniziali:
~(t = 0) = 0 ; d~(t = 0)/dt = n~(t = 0) = 0 ,
si ottiene:
D = p/s ;  = atan(ss) ,
da cui:
~(t) = 1 + (p/s)sin[st  atan(ss)]exp(t/s) .
A titolo di esempio, la fig. 20 mostra il transitorio dell’angolo di carico (t) = 1 + ~(t), supponendo:
Tp = 2/p = 1.5 s;  = 0.05; 1 = 20 ° ;  = 15 ° .
17
Macchina sincrona isotropa: note aggiuntive 50
[°] 40
t
30
20
18
0 Tp
10 t [s] 20
30
Fig. 20 – Transitorio dell’angolo di carico a seguito di un incremento della coppia motrice.
Ovviamente in assenza di fenomeni dissipativi (ks = 0   = 0) le oscillazioni non sono smorzate ed
hanno pulsazione p: a tali oscillazioni, dovute ad una brusca variazione della coppia esterna, si dà il
nome di oscillazioni proprie od oscillazioni libere:
~proprie(t) = [1  cos(pt)] .
Oltre alle oscillazioni proprie si possono avere anche oscillazioni forzate, che si verificano quando la
coppia esterna applicata all'albero della macchina è variabile periodicamente. Questo può avvenire in
diverse situazioni applicative, ad esempio:
 generatore sincrono azionato da un motore a moto alternativo (ad esempio un motore diesel);
 motore sincrono che aziona macchine operatrici a carico periodicamente variabile.
Nell'ipotesi di macchina in parallelo soggetta ad oscillazioni forzate di pulsazione f , è opportuno che
le pulsazioni p ed f siano sufficientemente diverse perché altrimenti le oscillazioni pendolari si
amplificano progressivamente (se lo smorzamento non è molto energico) e possono giungere a
superare il limite di stabilità, provocando la perdita di passo della macchina.
7. Funzionamento in parallelo alla rete e procedura di inserzione.
Il caso di un generatore sincrono isolato che alimenta il proprio carico in modo indipendente da altri
generatori si verifica in applicazioni particolari, di potenza generalmente limitata.
Nei sistemi di produzione e distribuzione dell'energia elettrica normalmente si hanno invece più
generatori sincroni collegati in parallelo alla rete.
Il collegamento in parallelo permette di soddisfare alle seguenti esigenze:
 realizzare le necessarie condizioni di stabilità del sistema;
 soddisfare facilmente, con l'inserimento di nuove macchine, la richiesta di aumento di potenza da
parte degli utenti della rete;
 consentire la disinserzione delle macchine, sia in caso di guasto che di manutenzione preventiva,
senza compromettere la continuità del servizio;
 fare lavorare solo una parte delle macchine quando si riducono le richieste di carico dell'utenza, in
modo tale che gli alternatori in esercizio possano funzionare sempre in condizioni prossime a
quelle nominali e quindi con un elevato valore del rendimento.
Il funzionamento in parallelo riguarda anche le macchine sincrone funzionanti come motori.
L'operazione di inserzione di una macchina sincrona in parallelo a una rete deve essere eseguita in
modo tale che alla chiusura dell'interruttore tripolare T (Fig. 20), che collega i morsetti della macchina
ad una rete già alimentata da uno o più generatori, non si manifesti nessuna perturbazione dello stato
di regime della rete, e non si verifichi nessuna circolazione transitoria di corrente negli avvolgimenti
della macchina a seguito della chiusura dell’interruttore di parallelo.
Perché ciò avvenga è necessario (prima di chiudere T) che la terna di f.e.m. a vuoto della macchina sia
in ogni istante uguale alla terna delle tensioni esistenti tra i conduttori della rete alla quale viene
Macchina sincrona isotropa: note aggiuntive connessa. Ciò si verifica se, per la terna di tensioni di rete e la terna di f.e.m. a vuoto della macchina,
risultano soddisfatte tutte le seguenti condizioni:
1. identità della frequenza;
2. identità dei valori efficaci;
3. concordanza di fase e del senso ciclico (le tensioni di a1, a2, a3 e di b1, b2, b3 costituiscono terne
entrambe di senso ciclico diretto).
Una volta soddisfatte le tre condizioni, l'interruttore T può essere chiuso e la macchina inserita in
parallelo alla rete.
Fig. 20 – Schema di principio relativo
all'inserzione di una macchina sincrona in
parallelo a una rete.
Da un punto di vista operativo, in linea di principio si può fare uso di tre lampade, dette lampade di
sincronismo, inserite tra i poli dell'interruttore. La procedura comprende la seguente sequenza di
operazioni, da eseguire con interruttore aperto (Fig. 20):
1. si porta la macchina in rotazione alla velocità N = 60f/n per avere una frequenza f uguale a quella
di rete (controllabile con due frequenzimetri);
2. si agisce sul circuito di eccitazione in modo di avere in uscita una f.e.m. a vuoto uguale alla
tensione di rete (verificabile con dei voltmetri derivati sulla linea e ai morsetti della macchina);
3. si controlla la concordanza di fase ed il senso ciclico (verificabile con le lampade di sincronismo).
Idealmente, quando le lampade rimangono permanentemente spente, la macchina è in sincronismo e
l'interruttore può essere chiuso. Tuttavia, finché T è aperto, è praticamente impossibile regolare la
velocità in modo che la frequenza sia permanentemente identica a quella di rete, con la conseguenza
che le lampade si accendono e si spengono alternativamente con una frequenza corrispondente alla
differenza tra la frequenza della rete e quella della macchina (fenomeno dei battimenti).
Portata la frequenza di battimento ad un valore molto basso mediante una regolazione fine della
velocità, si chiude comunque l'interruttore in un momento in cui le lampade appaiono spente: da
questo istante in poi, la macchina mantiene il sincronismo, dato che ogni eventuale variazione di
velocità rispetto al sincronismo verrebbe contrastata dall'interazione che nasce tra il campo di
induttore e quello di indotto.
Nella pratica, usualmente la procedura per inserire una macchina sincrona in parallelo alla rete è
automatizzata.
19
Macchina sincrona isotropa: note aggiuntive 8. Funzionamento da motore o generatore della macchina sincrona isotropa: il segno nella legge
della induzione elettromagnetica e le convenzioni tensione-corrente ai morsetti.
Si consideri che la macchina sincrona ruoti in senso
antiorario e si assuma un funzionamento da motore,
come mostrato in fig. 21: in base al principio di
allineamento, il fasore f.m.m. di indottoMI tende a
trascinare verso di sé il fasore f.m.m. di campoMC, e
quindi il rotore, che è il sostegno di tale f.m.m..
Allora, nelle condizioni assunte, la coppia
elettromagnetica Ce che agisce sul rotore (e quindi
suMC) è equiversa con la velocità; dunque, la coppia
elettromagnetica Ce è motrice mentre la coppia
meccanica all’albero Cm è frenante: pertanto, la
macchina funziona da motore (fig. 22, a sinistra).
Al contrario, sempre con macchina rotante in senso
antiorario, se la f.m.m. di indottoMI è in ritardo
rispetto aMC, la coppia elettromagnetica Ce che
agisce sul rotore (e quindi suMC) è opposta alla
velocità; dunque, Ce è frenante e Cm è motrice, cioè la
macchina funziona da generatore (fig. 22, a destra).
Dato che si sta considerando il funzionamento da
motore, è naturale trattare il circuito equivalente come
quello di un utilizzatore attivo, con le convenzioni
degli utilizzatori ai morsetti; la relativa legge alla
maglia dunque risulta (cfr. fig. 23):
Vf =Eo + (R + j X) I .
MI

Ce

MC
x
20
Fig. 21 – Posizione dei fasori spaziali f.m.m.
nel funzionamento da motore della macchina
sincrona isotropa.
MI
Ce

MC

Mot MC C
m
Gen
Cm
Ce
MI
Fig. 22 – Diagrammi fasoriali delle f.m.m. e
senso d’azione delle coppie sul rotore:
Ce = coppia elettromagnetica al traferro; Cm =
coppia meccanica all’albero; funzionamento
da motore (Mot) e da generatore (Gen).
I
R I
j X I
Per il circuito di fig. 23, il diagramma dei fasori
Eo
Vf
spazio-temporali risulta quello mostrato in fig. 24.
Si noti, che il legame fra il fasore f.e.m.E0 e il fasore
flusso concatenatoC è quello della legge della Fig. 23 – Circuito equivalente di una fase
induzione scritta con il segno positivo (il verso della della macchina sincrona, con la convenzione
degli utilizzatori ai morsetti.
f.e.m. agente nell’avvolgimento è associato al verso
del flusso con la regola della vite sinistrorsa):
j X I
E0 = + j C.
Si noti che in tal modo a vuoto risulta:Vf vuoto = +E0.
Si osservino ampiezza e verso degli angoli di fig. 24:
 l’angolo di carico δ è qui definito positivo come
l’angolo di rotazione del fasoreE0 per sovrapporsi
aVf; dunque, la coppia elettromagnetica
Ce = 3[(Vf E0)/(oX)]sin()
è positiva come coppia motrice e la potenza
meccanica Pm = Ce è positiva come erogata
all’albero dalla macchina.
 inoltre,  < 90°, per cui la potenza attiva ai morsetti
Pe = 3Vf Icos risulta positiva, che (con le
convenzioni adottate, cioè degli utilizzatori)
significa potenza attiva assorbita.
Vf
δ R I
Eo
I MI
φ

C
MC
Fig. 24 – Diagramma fasoriale del
funzionamento da motore, con le convenzioni
di fig. 23 e con la legge della induzione
scritta come:E0 = + j C.
Macchina sincrona isotropa: note aggiuntive Si consideri ora il funzionamento da generatore (cfr. fig.
25): continuando a mantenere le convenzioni degli

utilizzatori di fig. 23, il diagramma dei fasori spazioMC
temporali risulta quello rappresentato in fig. 26.

Si osservino ampiezza e verso degli angoli di fig. 26:
Ce
 l’angolo di carico δ (che, come prima, è definito
x
positivo come l’angolo di rotazione antioraria del
MI
fasoreE0 per sovrapporsi aVf) appare negativo (in
quanto misurato in senso orario): questo comporta Fig. 25 – Posizione dei fasori f.m.m. nel
funzionamento da generatore della
che la coppia elettromagnetica
macchina sincrona isotropa.
Ce = 3[(Vf E0)/(oX)]sin() ,
intesa come coppia motrice, in realtà è negativa e
dunque è una coppia resistente (a conferma del senso
d’azione in fig.25): pertanto, anche la potenza
meccanica Pm = Ce, misurata come erogata, in
realtà è assorbita all’albero della macchina;
 inoltre, poiché risulta  > 90°, la potenza attiva ai
morsetti Pe = 3Vf Icos, assunta positiva in quanto
assorbita (convenzioni di fig. 23), è in realtà
negativa, dunque erogata verso la rete interconnessa.
In queste condizioni (cioè nel funzionamento fisico da
generatore), risulta spontaneo far in modo che ogni
potenza venga misurata in modo tale da risultare
positiva: a tale scopo, mantenendo invariato il senso di
circolazione della correnteI (cui è associato anche il
verso spaziale della f.m.m.MI) e il verso dellaMC (cui
è legato il verso del fasore flusso concatenatoC), è
opportuno ribaltare la convenzione di misura del fasore
tensioneVf e del fasore f.e.m.E0, come mostrato nel
circuito equivalente mostrato in fig. 27 (cosicché nel
funzionamento a vuoto continui a risultare:Vf vuoto =
+E0). Naturalmente, il ribaltamento del fasore
f.e.m.E0 rispetto al verso di fig. 23 obbliga al
cambiamento di segno intrinseco, ovvero:
jXI
RI
Vf
Eo
δ
I
φ C
MC

MI
Fig. 26 – Diagramma fasoriale del
funzionamento da generatore, con le
convenzioni di fig. 23 e con la legge della
induzione scritta come:E0 = + j C.
I
E0 =  j C ,
Vf
R I
j X I
Eo
che corrisponde ad applicare la legge della induzione Fig. 27 – Circuito equivalente di una fase
legando il verso della f.e.m. nell’avvolgimento al verso della macchina sincrona, con la
convenzione dei generatori ai morsetti.
del flusso con la regola della vite destrorsa.
Con i versi di fig. 27, la legge delle tensioni risulta:
Vf =E0  (R + j X) I .
In conclusione, pur non essendo obbligatorio, risulta opportuno studiare il funzionamento dei
generatori adottando la formulazioneE0 =  j C , mentre per lo studio dei motori è più
conveniente la formulazioneE0 = + j C .
21