TIPI DI TRIANGOLO

TIPI DI TRIANGOLO
La classificazione dei triangoli può essere fatta o in
riferimento ai lati oppure agli angoli.
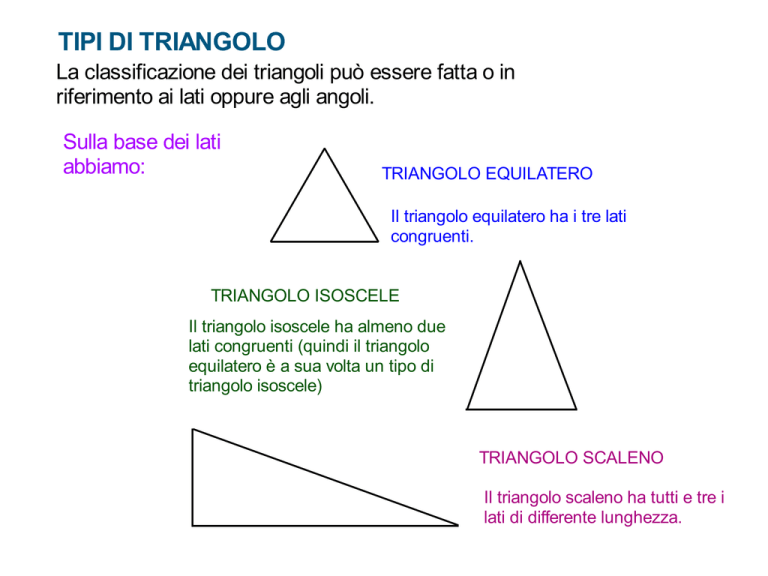
Sulla base dei lati
abbiamo:
TRIANGOLO EQUILATERO
Il triangolo equilatero ha i tre lati
congruenti.
TRIANGOLO ISOSCELE
Il triangolo isoscele ha almeno due
lati congruenti (quindi il triangolo
equilatero è a sua volta un tipo di
triangolo isoscele)
TRIANGOLO SCALENO
Il triangolo scaleno ha tutti e tre i
lati di differente lunghezza.
SULLA BASE DEGLI ANGOLI ABBIAMO:
TRIANGOLI ACUTANGOLI
tutti gli angoli sono minori di 90°
TRIANGOLI RETTANGOLI
hanno un angolo di 90° (angolo retto).
I triangoli rettangoli possono essere scaleni
oppure isosceli.
TRIANGOLI OTTUSANGOLI
hanno un angolo maggiore di 90°
(angolo ottuso).
I PUNTI NOTEVOLI DEL
TRIANGOLO
ALTEZZE DEL TRIANGOLO
in un triangolo si chiama ALTEZZA il segmento che partendo da un
vertice forma un angolo di 90° (un angolo retto) con il lato opposto.
Questa altezza si dice RIFERITA a questo lato opposto.
B
altezza riferita a BC
A
proiezione di AC
proiezione
di AB
piede dell'altezza
H
C
Il segmento AH, che partendo dal vertice A forma un angolo retto
con il lato opposto BC si dice ALTEZZA RIFERITA AL LATO BC. Il
punto H si dice PIEDE DELL'ALTEZZA AH, i segmenti BH e HC si
dicono rispettivamente proiezioni dei lati AB e AC sul lato BC (base
del triangolo).
In un triangolo ci sono tre lati e tre vertici, per cui abbiamo anche TRE
altezze, come mostra la figura qui sotto.
Il triangolo ABC possiede tre altezze:
1) altezza AH riferita al lato BC
2) altezza BK riferita al lato AC
3) altezza CS riferita al lato AB
B
A
K
S
O
H
Le tre altezze di un triangolo si incontrano in un unico punto chiamato
ORTOCENTRO (O).
L'Ortocentro è il punto di incontro delle tre altezze di un triangolo.
C
OSSERVAZIONI SULLE ALTEZZE E
SULL'ORTOCENTRO DEL TRIANGOLO
La posizione dell'ortocentro dipende dal tipo di triangolo.
Se disegnamo le tre altezze di un qualunque tipo di triangolo (acutangolo,
ottusangolo, rettangolo...) possiamo osservare la posizione dell'ortocentro.
Nei triangoli acutangoli l'ortocentro è
SEMPRE INTERNO AL TRIANGOLO.
TRIANGOLI
OTTUSANGOLI
Nei triangoli ottusangoli le altezze
formano un angolo retto con il lato
opposto o con il suo
prolungamento. L'ortocentro è
sempre esterno al triangolo.
ALTEZZE E ORTOCENTRO NEI TRIANGOLI
RETTANGOLI.
ortocentro
alte
all' zza
ipo rife
ten rita
usa
cateto
ALTEZZE E ORTOCENTRO NEI
TRIANGOLI RETTANGOLI
Ip o
ten
usa
cateto
Nei triangoli rettangoli due delle tre altezze coincidono con i
lati più piccoli, chiamati cateti, la terza altezza parte da un
vertice (quello formato dai due cateti) e forma un angolo retto
con il lato maggiore, chiamato IPOTENUSA.
L'ortocentro coincide con il vertice opposto all'ipotenusa, cioè
quello che forma un angolo di 90 gradi.
CONCLUSIONI
1) L'altezza di un triangolo relativa a un lato è il segmento che partendo
dal vertice opposto forma un agolo di 90 gradi con lo stesso lato (cioè, il
segmento perpendicolare al lato di riferimento o al suo prolungamento,
che parte dal vertice opposto).
2) Le tre altezze di un triangolo si incontrano in un unico punto
chiamato ortocentro (O), che può essere interno (nei triangoli
acutangoli), esterno (nei triangoli ottusangoli), oppure coincidente con il
vertice dell'angolo retto nei triangoli rettangoli.
LA BISETTRICE DI
UN ANGOLO
ce
i
r
t
t
e
bis
vertice
A
LE TRE BISETTRICI DI UN
TRIANGOLO
Le tre bisettrici si incontrano in un
unico punto chiamato INCENTRO
L'incentro si trova
sempre all'interno
del triangolo
incentro (I)
B
L'incentro si trova sempre alla
stessa distanza dai tre lati.
C
1) La bisettrice di un triangolo relativa a un determinato angolo è il segmento di
bisettrice che lo divide in due parti uguali.
2) Un triangolo ha tre bisettrici, che si incontrano in un solo punto chiamato
INCENTRO.
3) l'INCENTRO è sempre interno al triangolo, ed è equidistante dai tre lati.
LE TRE MEDIANE DI UN TRIANGOLO E
IL BARICENTRO
Si dice MEDIANA il segmento che partendo da un vertice raggiunge il punto
medio del lato opposto. Il punto medio di un lato è quello che lo divide in due
parti uguali.
Le tre mediane di un triangolo si
A
incontrano in un punto che si chiama
BARICENTRO, che è sempre INTERNO
al triangolo.
BARICENTRO (B)
In qualunque triangolo il
BARICENTRO divide ciascuna
mediana in due parti, una delle
quali è la metà dell'altra.
B
C
Il BARICENTRO è il CENTRO DI GRAVITA' del triangolo, cioè il
suo PUNTO DI EQUILIBRIO.
GLI ASSI DI UN TRIANGOLO E IL CIRCOCENTRO
Si dice ASSE di un lato la retta che, passando per il suo punto medio,
forma un angolo di 90 gradi con il lato stesso.
Poichè un triangolo possiede tre lati, allora presenta anche
TRE ASSI.
A
I tre assi di un triangolo si
incontrano in un punto chiamato
CIRCOCENTRO
CIRCOCENTRO (C)
B
C
OSSERVAZIONI SUGLI ASSI E SUL CIRCOCENTRO
La posizione del circocentro dipende dal tipo di
triangolo.
Nei triangoli acutangoli il circocentro
è interno al triangolo
Il circocentro è
sempre equidistante
dai vertici
C
Nel triangolo rettangolo la posizione del circocentro coincide
con il punto medio del lato maggiore (ipotenusa)
A
circocentro
B
C
NEI TRIANGOLI OTTUSANGOLI IL CIRCOCENTRO E'
SEMPRE ESTERNO AL TRIANGOLO
In un qualunque
triangolo il circocentro è
equidistante dai tre
vertici.
A
a = b = c
a
b
B
c
C
Nel triangolo equilatero, ortocentro,
incentro, baricentro e circocentro
coincidono!
NEL TRIANGOLO ISOSCELE
ORTOCENTRO, INCENTRO,
BARICENTRO E CIRCOCENTRO NON
COINCIDONO MA SI TROVANO
ALLINEATI.
Circocentro
Baricentro
Incentro
Ortocentro
CRITERI DI CONGRUENZA
Abbiamo visto che due angoli si dicono
congruenti se sono perfettamente
sovrapponibili.
In generale, diremo che due figure geometriche
sono congruenti quando sono perfettamente
sovrapponibili.
Prendiamo due figure poligonali,
F ed F'
A
C
A'
B
C'
G
F
B'
G'
F'
F'
F
D
D'
E
E'
DUE FIGURE PIANE F ED F' SONO CONGRUENTI SE, SOVRAPPONENDOLE
MEDIANTE UNO O PIU' MOVIMENTI CHE NON LE DEFORMINO, COINCIDONO
PERFETTAMENTE.
A
A'
B
C
C'
G
G'
B'
F F'
D
D'
E
E'
per esempio, due triangoli sono CONGRUENTI
se, sovrapposti, coincidono perfettamente.