Esercizio 1 - Discesa libera
Uno sciatore di 77 kg è fermo sulla cima di una collina che ha un’altezza di 50 m rispetto al
fondo valle. Inizia a scendere lungo una discesa inclinata di 30◦ , arriva a valle e poi risale verso
un altra collina alta 40 m. Trascurando le forze di attrito,
a. quanto vale la velocità dello sciatore nel momento in cui transita per il fondo valle?
b. quanto vale la sua velocità sulla cima della seconda collina?
c. l’angolo di inclinazione della prima collina influenza il risultato? E la massa dello sciatore?
Svolgimento con commento
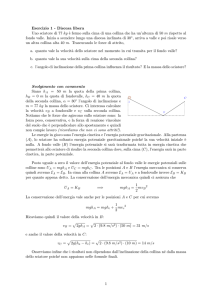
Siano hA = 50 m la quota della prima collina, hB =
0 m la quota di fondovalle, hC = 40 m la quota della secC
onda collina, α = 30◦ l’angolo di inclinazione e m = 77 kg
A
la massa dello sciatore. Ci interessa calcolare la velocità
vB a fondovalle e vC sulla seconda collina. Notiamo che
B
le forze che agiscono sullo sciatore sono: la forza peso,
conservativa, e la forza di reazione vincolare del suolo che
è perpendicolare allo spostamento e quindi non compie
lavoro (ricordiamo che non ci sono attriti!).
Le energie in gioco sono l’energia cinetica e l’energia potenziale gravitazionale. Alla partenza
(A), lo sciatore ha soltanto energia potenziale gravitazionale poiché la sua velocità iniziale è
nulla. A fondo valle (B) l’energia potenziale si sarà trasformata tutta in energia cinetica che
permetterà allo sciatore di risalire la seconda collina dove, sulla cima (C), l’energia sarà in parte
cinetica, in parte potenziale.
Posto uguale a zero il valore dell’energia potenziale al fondo valle le energie potenziali sulle
colline sono UA = mghA e UC = mghC . Tra le posizioni A e B l’energia meccanica si conserva
quindi avremo EA = EB . In cima alla collina A avremo EA = UA e a fondovalle invece EB = KB
per quanto appena detto. La conservazione dell’energia meccanica quindi ci assicura che
UA = KB
1
mghA = mvB 2
2
=⇒
La conservazione dell’energia vale anche per le posizioni A e C per cui avremo
1
mghA = mghc + mvc 2
2
Ricaviamo quindi il valore della velocità in B:
q
p
vB = 2ghA = 2 · (9.8 m/s2 ) · (50 m) = 31 m/s
e anche il valore della velocità in C:
q
p
vC = 2g(ha − hc ) = 2 · (9.8 m/s2 ) · (10 m) = 14 m/s
Osserviamo infine che i risultati non dipendono dall’inclinazione della collina né dalla massa
dello sciatore poiché non appaiono nelle formule finali.
1