Università degli Studi di Padova
Facoltà di Scienze Politiche
STATISTICA
DEC curr. Impresa (sede di Rovigo)
Prova scritta del 06/02/2007
[19pt]
(DEC060207.tex)
1) La seguente tabella riporta alcuni dati relativi alla diffusione di tecnologia informatica nelle famiglie
italiane nel 2006. Fonte: “ Le tecnologie dell’informazione e della comunicazione: disponibilità nelle
famiglie e utilizzo degli individui. Periodo di riferimento: Anno 2006” , www.ISTAT.it. In particolare,
in alcune regioni italiane, sono state rilevate le seguenti variabili statistiche:
1X :
2X :
3X :
4X :
5X :
6X :
7X :
8X :
9X :
10 X :
11 X :
percentuale di famiglie che dispone a casa propria di un Personal Computer;
percentuale di famiglie che dispone a casa propria di una connessione a banda larga;
percentuale di famiglie che dispone a casa propria di accesso ad Internet;
percentuale di persone che hanno utilizzato Internet per cercare informazioni su merci e servizi;
percentuale di persone che hanno utilizzato Internet per mandare o ricevere email;
percentuale di persone che hanno utilizzato Internet per telefonare su Internet, partecipare a videoconferenze;
percentuale di persone che hanno utilizzato Internet per usare servizi relativi a viaggi e soggiorni;
percentuale di persone che hanno utilizzato Internet per usare servizi bancari online;
percentuale di persone che hanno utilizzato Internet per leggere o scaricare giornali, news, riviste;
percentuale di persone che hanno utilizzato Internet per giocare o scaricare giochi, immagini, musica;
percentuale di persone che hanno utilizzato Internet per ordinare o comprare merci e/o servizi su Internet
negli ultimi 12 mesi.
Regione
Valle d’Aosta
Lombardia
Trentino Alto-Adige
Veneto
Friuli-Venezia Giulia
Liguria
Lazio
Molise
Campania
Puglia
Sicilia
Sardegna
1X
2X
3X
4X
5X
6X
7X
8X
9X
10 X
11 X
46.9
52.1
52.3
48.6
47.3
40.2
48.5
47.4
41.6
40.6
37.6
49.4
12.3
16.9
17.5
14.7
18.6
15.9
18.0
8.6
11.2
12.3
11.4
13.4
34.1
42.0
39.4
38.3
36.7
31.7
39.9
34.0
29.0
28.7
26.6
36.8
63.6
65.4
63.9
63.9
66.5
65.7
60.6
63.5
47.2
50.6
51.4
61.2
76.9
80.1
78.4
78.1
80.3
78.8
78.4
71.4
68.0
69.0
70.2
71.9
5.9
8.3
8.4
6.8
8.2
8.6
12.7
7.7
11.2
7.8
6.1
7.5
38.5
44.7
37.6
43.4
39.0
39.6
40.7
30.0
31.9
32.2
30.7
36.8
26.4
30.2
27.0
27.5
25.9
19.8
24.5
13.2
12.2
12.9
13.9
19.7
26.8
35.1
34.1
36.6
31.7
34.4
39.5
33.7
31.4
29.5
29.9
30.7
28.3
31.5
28.5
31.2
31.5
34.0
34.2
37.8
38.1
33.0
33.0
33.1
25.4
23.7
28.1
23.5
26.3
21.2
20.3
18.8
13.2
16.1
13.7
22.8
[1pt]
1.1) Indicare qual è l’unità statistica, la natura delle variabili e su quale scala sono misurate.
[2pt]
1.2) Si calcolino la mediana e il quantile 2 x0.25 della variabile 2 X.
[2pt]
1.3) Si confronti la variabilità di 4 X con la variabilità di
rimento: 4 σ 2 =40.53909722).
[2pt]
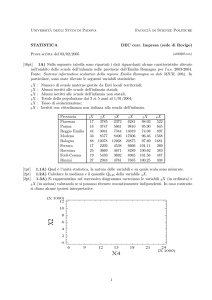
1.4) Si rappresentino in un diagramma cartesiano le variabili 11 X, (in ordinata) e 4 X, (in ascissa) valutando se si possano ritenere stocasticamente indipendenti. In caso contrario si diano alcune ipotesi
interpretative.
[1pt]
11 X,
commentando opportunamente (sugge-
1.5) Si determinino, nell’ambito del principio dei minimi quadrati, i parametri del modello di regressione
11 X
(suggerimento:
= α0 + α1 4 X + ε.
4,11 σ=25.48743056).
1
[2pt]
[3pt]
1.6) Si valuti il grado di adattamento relativo della retta di regressione calcolata al punto precedente,
con opportuni commenti critici. Inoltre, si rappresenti graficamente la retta di regressione sul diagramma cartesiano prodotto al punto 1.4).
1.7) Se si adatta ai dati, secondo i minimi quadrati, un piano di regressione inserendo la variabile 7 X,
si ottiene il seguente risultato:
11 X
∗
= −18.1189 + 0.533551 4 X + 0.189852 7 X.
Calcolare la varianza residua intorno a questo modello e quantificare il miglioramento rispetto al modello lineare di cui al punto 1.4) (Suggerimento: 11 X 7 X σ = Cov(11 X, 7 X) = 797.3591667).
[1pt]
1.8) Si determini una opportuna media dei residui relativi al modello del punto 1.5).
[1pt]
1.9) Si determini il residuo per la regione Molise relativo al modello del punto 1.5), commentando
opportunamente il valore ottenuto.
[2pt]
1.10) Se si studia la regressione multipla, secondo i minimi quadrati, del carattere
restanti caratteri, attraverso il modello (ME)
11 X
11 X
su alcuni dei
= α0 + α1 1 X + α2 2 X + α3 3 X + α4 4 X + α7 7 X + α8 8 X + α10 10 X + ε,
si ottengono i risultati che seguono, ove, tra parentesi tonde, figura la statistica t:
α̂0 = −28.2765 (−2.9811); α̂1 = 1.51981 (5.35533); α̂2 = 0.702921 (4.85952); α̂3 = −1.59846 (−4.33478);
α̂4 = 0.449773 (8.66322); α̂7 = 0.307159 (1.78038); α̂8 = −0.10851 (−0.590657);
2
pari a 0.992593.
α̂10 = −0.342745 (−1.99325) con un valore di 11 X RME
Commentare i risultati ottenuti precisando il grado di attendibilità del modello proposto, la differente
rilevanza delle componenti esplicative adottate, valutando la possibilità di operare riduzioni del modello.
[2pt]
1.11) Se si esclude dal modello precedente la componente relativa a 8 X e si stima il modello (Mrid)
11 X
= α0 + α1 1 X + α2 2 X + α3 3 X + α4 4 X + α7 7 X + α10 10 X + ε,
si ottengono i risultati che seguono, ove, tra parentesi tonde, figura la statistica t:
α̂0 = −28.0234 (−3.17111); α̂1 = 1.49032 (5.72005); α̂2 = 0.687374 (5.18189);
α̂3 = −1.60652 (−4.6746); α̂4 = 0.44124 (9.48769); α̂7 = 0.237201 (2.02749);
2
α̂10 = −0.268899 (−2.44234) con un valore di 11 X RMrid
pari a 0.991947.
Interpretare i risultati riferendosi esplicitamente al contesto reale descritto al punto 1), precisando il grado di attendibilità del modello ottenuto e la possibilità di operare ulteriori riduzioni nel
modello stesso.
2
[8pt]
2) Nella seguente tabella è riportata la distribuzione delle regioni italiane suddivise per fascia di spesa
media mensile delle famiglie per capitolo di spesa alimentare, X, e non alimentare, Y (Fonte: ISTAT,
Annuario Statistico Italiano, dati in euro, anno di riferimento 2004).
X: alimentari
395 a 434
434 a 473
473 a 512
Totale
1200 a
2
3
1
6
Y : non alimentari
1600 1600 a 2000 2000
0
4
1
5
a 2400
4
4
1
9
Totale
6
11
3
20
[1pt]
2.1) Si individuino l’unità statistica, la natura e la scala di misurazione delle variabili rilevate.
[3pt]
2.2) Calcolare le distribuzioni di frequenza relativa della variabile X condizionate alla prima e alla
seconda modalità di Y . Attraverso un’opportuna rappresentazione grafica, effettuare un confronto fra
le due distribuzioni ottenute e commentare il risultato.
[1pt]
2.3) Giustificando la risposta, valutare se esista indipendenza stocastica tra le variabili X e Y.
[3pt]
2.4) Si calcoli e si commenti opportunamente il valore dell’indice di connessione di Pearson χ2 tra la
variabile Y e la variabile X, ricorrendo ad una opportuna normalizzazione.
[4pt]
3) Si consideri una variabile statistica doppia (X, Y ) a componenti quantitative non incorrelate. Siano
Ŷ = â + b̂X,
e
X̂ = α̂ + β̂Y
le due possibili rette di regressione con parametri calcolati con il metodo dei minimi quadrati:
il segno del parametro b̂ deve coincidere con quello del parametro β̂.
[3pt]
3.1) Si provi l’affermazione precedente.
[1pt]
3.2) Si dia una interpretazione informale dell’affermazione precedente.
[3pt]
4) Si consideri una variabile statistica quantitativa doppia (X, Y ). Si spieghi per quale ragione la quantità
s
p
1 X 2
ei
RMSE = Y σ 1 − ρ2 =
N
i
possa essere utilizzata come riferimento per l’ordine di grandezza dei residui ei della retta di regressione
Y ∗ = αo∗ + α1∗ X.
3