Università degli Studi di Padova
Facoltà di Scienze Politiche
STATISTICA
DEC curr. Impresa (sede di Rovigo)
Prova scritta del 28/06/2006
[25pt]
(DEC280606.tex)
1) La seguente tabella riporta alcuni dati relativi alle case occupate nel Comune di Roma (dati rilevati attraverso il
censimento 1991). Fonte: www.comune.roma.it. In particolare, per alcuni municipi della città di Roma sono state
rilevate le seguenti variabili statistiche:
1 X : superficie media degli appartamenti occupati;
2 X : numero di stanze medio degli appartamenti occupati;
3 X : numero di occupanti medio per appartamento occupato;
4 X : percentuale di appartamenti abitati da proprietari;
5 X : percentuale di appartamenti abitati da affittuari.
Municipio
1X
2X
3X
4X
5X
I
91.1 4.1 2.1 49.2 43.8
II
105.7 4.6 2.3 62.5 30.1
III
90.9 4.1 2.2 62.4 31.5
IV
85.8 4.0 2.8 54.0 41.7
V
78.9 3.8 2.9 53.1 42.9
VI
74.1 3.6 2.6 62.5 33.2
VII
70.1 3.5 2.8 59.8 35.9
VIII
83.2 3.9 3.1 58.1 35.3
IX
80.8 3.8 2.4 64.2 30.6
[1pt]
1.1) Indicare qual è l’unità statistica, la natura delle variabili e su quale scala sono misurate.
[2pt]
1.2) Si calcolino la mediana e il quantile 2 x0.25 della variabile 2 X.
[2pt]
[2pt]
1.3) Si confronti la variabilità di 2 X con la variabilità di 3 X, commentando opportunamente.
1.4) Si costruisca un box and whiskers plot della variabile 2 X (suggerimento: 2 x0.75 = 4.1.)
3.4 3.5 3.6 3.7 3.8 3.9 4.0 4.1 4.2 4.3 4.4 4.5 4.6 4.7
2X
[2pt]
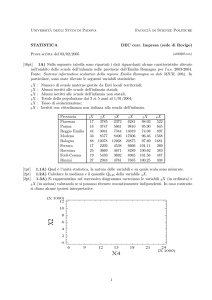
1.5) Si rappresentino in un diagramma cartesiano le variabili 3 X, numero medio di occupanti per appartamento, (in
ordinata) e 2 X, numero medio di stanze, (in ascissa) valutando se si possano ritenere stocasticamente indipendenti.
In caso contrario si diano alcune ipotesi interpretative.
[3pt]
1.6) Si valuti l’intensità della eventuale dipendenza in media di 3 X da 2 X mediante il rapporto di correlazione η32X/2 X
e si commenti il valore ottenuto.
[1pt]
1.7) Si determinino, nell’ambito del principio dei minimi quadrati, i parametri del modello di regressione
3X
= α0 + α1 2 X + ε.
[2pt]
1.8) Si valuti il grado di adattamento relativo della retta di regressione calcolata al punto precedente, con opportuni
commenti critici. Inoltre, si rappresenti graficamente la retta di regressione sul diagramma cartesiano prodotto al
punto 1.5).
[3pt]
1.9) Se si adatta ai dati un piano di regressione inserendo anche la variabile 1 X, superficie media, si ottiene il seguente
risultato:
∗
3 X = −8.037817 − 0.2916207 1 X + 8.964606 2 X,
la cui varianza residua è pari a 0.025425604. Quantificare il miglioramento rispetto al modello lineare di cui al
punto 1.7) commentando opportunamente.
1
[3pt]
1.10) Calcolare il coefficiente di correlazione parziale fra 3 X e 1 X al netto dell’influenza esercitata su entrambe da 2 X.
[2pt]
1.11) Se si studia la regressione multipla, secondo i minimi quadrati, del carattere 3 X su alcuni dei restanti caratteri,
attraverso il modello
3X
= α0 + α1 1 X + α2 2 X + α4 4 X + α5 5 X + α6 (1 X ∗ 2 X) + α7 (4 X ∗ 5 X) + ε,
si ottengono i risultati che seguono, ove, tra parentesi tonde, figura la statistica t:
αˆ0 = 6, 86229 (0, 742441); αˆ1 = −0, 269938 (−3, 4308); αˆ2 = 13, 6356 (4, 3546);
αˆ4 = −0, 352832 (−3, 26481); αˆ5 = −0, 469758 (−2, 83734); αˆ6 = −0, 0261566 (−2, 45576); αˆ7 = 0, 00539263 (1, 64935);
con un valore di 3 X R12X,2 X,4 X,5 X,1 X∗2 X,4 X∗5 X pari a 0.980115.
Commentare i risultati ottenuti precisando il grado di attendibilità del modello proposto, la differente rilevanza
delle componenti esplicative adottate, valutando la possibilità di operare riduzioni del modello.
[2pt]
1.12) Se si esclude dal modello precedente la componente relativa all’interazione (4 X ∗ 5 X) e si stima il modello
3X
= α0 + α1 1 X + α2 2 X + α4 4 X + α5 5 X + α6 (1 X ∗ 2 X) + ε,
si ottengono i risultati che seguono, ove, tra parentesi tonde, figura la statistica t:
αˆ0 = −4, 74025 (−0, 630309); αˆ1 = −0, 35962 (−5, 04125); αˆ2 = 16, 9911 (5, 69044);
αˆ4 = −0, 198177 (−2, 94034); αˆ5 = −0, 211911 (−3, 09922); αˆ6 = 0, 0294866 (−2, 24774); con un valore di
R12X,2 X,4 X,5 X,1 X∗2 X pari a 0.953068. Interpretare i risultati riferendosi esplicitamente al contesto rea3X
le descritto al punto 1), precisando il grado di attendibilità del modello ottenuto e la possibilità di operare
ulteriori riduzioni nel modello stesso.
[9pt]
2) Nella seguente tabella viene riportato il movimento in arrivo di alcuni clienti stranieri negli esercizi alberghieri
della città di Roma secondo la provenienza del turista e la categoria dell’albergo. Anno 2004 (dati in migliaia).
Fonte: Comune di Roma. Annuario Statistico 2004.
X: Categoria
5 stelle
4 stelle
3 stelle
2 stelle
1 stella
Totale
Y : Provenienza
Centro/Sud America Medio Oriente
10
10
66
29
93
23
12
3
3
1
184
66
Australia
3
23
27
3
1
57
Totale
23
118
143
18
5
307
[1pt]
2.1) Si individuino l’unità statistica, la natura e la scala di misurazione delle variabili rilevate.
[1pt]
2.2) Calcolare, se possibile, moda, mediana e media aritmetica di X e Y .
[3pt]
2.3) Calcolare, rappresentare graficamente e confrontare le distribuzioni di frequenza relativa della variabile X, Categoria alberghiera, per il Centro/Sud America e per il Medio Oriente, commentando opportunamente i risultati
ottenuti.
[1pt]
2.4) Calcolare e commentare opportunamente il grado di mutabilità della variabile Y , Provenienza.
[1pt]
2.5) Si valuti se tra Categoria Alberghiera e Provenienza si possa affermare l’esistenza di indipendenza stocastica.
[2pt]
2.6) Si valuti se la Categoria Alberghiera dipenda dalla Provenienza. (Suggerimento:
base e, XY H = 0.905606 con log in base 10).
XY
H = 2.085236 con log in
[4pt]
3) Si consideri una variabile statistica quantitativa doppia (X, Y ). Se la funzione di regressione di Y su X è una retta
con inclinazione positiva, posso dire che ηY2 |X = 1? Perché?
[5pt]
4) Si consideri una variabile statistica quantitativa doppia (X, Y ). Si spieghi per quale ragione la scelta di un modello
di previsione P, per prevedere Y sulla base delle informazioni contenute in X, possa essere effettuata attraverso la
minimizzazione della devianza
N
X
δ 2 (P ) =
[yi − P (xi )]2 .
i=1
2