2.14 Il gradiente

2.14
Il gradiente
Introduciamo un importantissimo operatore differenziale, il gradiente e ne studiamo alcune proprietà. Esso è molto importante sia nella relazione tra energia
potenziale e campo di forze (che sviluppiamo poco) sia nello studio delle forze
di pressione nei fluidi in equilibrio (fluidostatica), dove lo useremo abbastanza
estensivamente. Esso è anche importante nella lettura di una mappa topografica.
Per studiare il gradiente, dobbiamo anticipare la definizione di derivata parziale, che verrà studiata nel corso di Matematica II ed è trattata nel testo di
Bianchi e Paparoni a pagina 272, definizione 13.8.
Qui riassumo brevemente supponendo che non si abbiano in mano i testi dei
corsi del secondo anno.
Consideriamo una funzione f definita in una regione R dello spazio, f =
f (x, y, z). Fissiamo un punto di coordinate x, y, z. Se valutiamo la funzione f
per y e z fissati, y = y e z = z e consideriamo variabile la sola x, f = f (x, y, z)
otteniamo una funzione della sola variabile x, chiamiamola temporaneamente g,
g = g(x) = f (x, y, z).
Supponiamo
che questa funzione g sia derivabile per x = x, esista la derivata
dg(x) . Questa derivata è chiamata derivata parziale della funzione f (x, y, z)
dx x=x
rispetto alla variabile x calcolata nel punto di coordinate x, y, z; essa dunque è
la derivata ordinaria della funzione f rispetto alla variabile x calcolata tenendo
fissi i valori delle variabili y e z.
Il simbolo della derivata parziale della funzione f rispetto alla variabile x calcolata nel punto di coordinate x, y, z è il seguente:
∂f (x, y, z) .
∂x
x,y,z
Ancora in parole, la derivata parziale rispetto alla variabile x è il limite del
rapporto incrementale ottenuto dando un incremento h alla sola x, limite per
l’incremento che tende a zero, in formula:
∂f (x, y, z) f (x + h, y, z) − f (x, y, z)
= lim
.
(2.192)
h→0
∂x
h
x,y,z
Le derivate parziali rispetto alle variabili y e z si definiscono analogamente:
∂f (x, y, z) f (x, y + h, z) − f (x, y, z)
= lim
,
(2.193)
h→0
∂y
h
x,y,z
f (x, y, z + h) − f (x, y, z)
∂f (x, y, z) = lim
.
(2.194)
h→0
∂z
h
x,y,z
Con i simboli
∂f (x, y, z)
,
∂x
∂f (x, y, z)
,
∂y
∂f (x, y, z)
,
∂z
si intende la valutazione delle derivate parziali in un punto non specificato.
95
Dalle definizioni, è possibile vedere il seguente fatto, importantissimo. Valutiamo la funzione f in un qualche punto (x, y, z); diamo un incremento ∆x
alla variabile x, senza variare le altre due variabili. Se la funzione ammette
la derivata parziale rispetto alla x nel punto considerato, la variazione f (x +
∆x, y, z) − f (x, y, z) della funzione f è data dall’espressione:
f (x + ∆x, y, z) − f (x, y, z) =
∂f (x, y, z)
∆x + errore(∆x)
∂x
(2.195)
dove il termine errore(∆x) tende a zero più rapidamente di ∆x:
lim
∆x→0
errore(∆x)
=0
∆x
Quindi la variazione f (x + ∆x, y, z) − f (x, y, z) della funzione f è approssimata
∆x:
dall’espressione ∂f (x,y,z)
∂x
f (x + ∆x, y, z) − f (x, y, z) ≈
∂f (x, y, z)
∆x
∂x
(2.196)
L’errore che si commette usando questa approssimazione è precisamente pari a
errore(∆x); ma, quanto più piccolo è l’incremento ancor più piccolo è l’errore.
Quando decidiamo che l’errore è trascurabile43 e quindi consideriamo la relazione approssimata come se fosse esatta, dobbiamo usare la notazione differenziale,
proprio per rammentare che abbiamo convenuto di trascurare l’errore. Indichiamo la variazione della variabile x con dx, invece che con ∆x o h o altro, e con
df (x, y, z) la variazione della funzione, df (x, y, z) = f (x + dx, y, z) − f (x, y, z)
e scriviamo l’uguaglianza:
df (x, y, z) =
∂f (x, y, z)
dx
∂x
(2.197)
invece della relazione (2.196).
Analogamente, per il caso in cui la variazione interessi la sola variabile y
oppure la sola variabile z abbiamo le formule:
∂f (x, y, z)
∆y + errore(∆y) ,
∂y
∂f (x, y, z)
f (x, y, z + ∆z) − f (x, y, z) =
∆z + errore(∆z) ,
∂z
f (x, y + ∆y, z) − f (x, y, z) =
(2.198)
(2.199)
le formule approssimate
∂f (x, y, z)
∆y ,
∂y
∂f (x, y, z)
f (x, y, z + ∆z) − f (x, y, z) ≈
∆z ,
∂z
f (x, y + ∆y, z) − f (x, y, z) ≈
(2.200)
(2.201)
43 Non importa che sia espresso da un numero piccolo o grande, l’importante è che sia
trascurabile per le considerazioni che facciamo nel caso specifico.
96
e le formule nella notazione differenziale per cui si è stabilito di considerare le
formule approssimate come se fossero esatte:
∂f (x, y, z)
dy
∂y
∂f (x, y, z)
df (x, y, z) =
dz .
∂z
df (x, y, z) =
(2.202)
(2.203)
Quando si variano contemporaneamente le tre variabili, o anche solo due
di esse, occorre aggiungere qualche condizione un po’ più restrittiva della sola
esistenza delle tre derivate parziali44 , dopodiché si hanno le formule analoghe
alle precedenti:
f (x + ∆x, y + ∆y, z + ∆z) − f (x, y, z) =
=
∂f (x, y, z)
∂f (x, y, z)
∂f (x, y, z)
∆x +
∆y +
∆z + errore(∆x, ∆y, ∆z)
∂x
∂y
∂z
(2.204)
dove il termine errore(∆x, ∆y, ∆z) tende a zero più rapidamente della lunghezza
((∆x)2 + (∆y)2 + (∆z)2 )1/2 dell’incremento complessivo delle tre variabili; si ha
la formula approssimata
f (x + ∆x, y + ∆y, z + ∆z) − f (x, y, z) ≈
≈
∂f (x, y, z)
∂f (x, y, z)
∂f (x, y, z)
∆x +
∆y +
∆z
∂x
∂y
∂z
(2.205)
e la formula con la notazione differenziale, con cui si intende di considerare
esatta l’approssimazione (2.205) qui sopra:
df (x, y, z) =
∂f (x, y, z)
∂f (x, y, z)
∂f (x, y, z)
dx +
dy +
dz
∂x
∂y
∂z
(2.206)
Abbiamo visto la definizione delle derivate parziali rispetto alle variabili x,
y e z, formule (2.192), (2.193), (2.194).
Inoltre abbiamo visto il modo più semplice per esprimere l’approssimazione dela
variazione di una funzione f (x, y, z) quando si variano le coordinate da x, y, z a
x + ∆x, y + ∆y, z + ∆z, formula (2.205) e la variazione della funzione quando
si decide che l’errore di questa approssimazione va trascurato e posto uguale a
zero e si usa quindi la notazione differenziale, formula (2.206).
Ora anticipiamo, con linguaggio necessariamente diverso ed elementare, parte del § 13.2 del testo di Bianchi e Paparoni e in particolare il gradiente (definito
nell’osservazione 13.4 del testo citato).
Riscriviamo le equazioni (2.205), (2.205), (2.205) con la notazione vettoriale.
44 Comunque, per quel che riguarda la Fisica I, possiamo supporre che le condizioni tali che
valgano le formule seguenti siano sempre soddisfatte.
97
Per farlo, introduciamo l’importantissimo vettore gradiente della funzione f
indicato con la notazione grad f (x, y, z) e dato dall’espressione
→
→ ∂f (x, y, z) −
→ ∂f (x, y, z) −
∂f (x, y, z) −
→
grad f (−
x)=
k .
i +
j +
∂x
∂y
∂z
(2.207)
Dunque il gradiente della funzione f è un campo vettoriale 45 le cui componenti
sono le seguenti.
1. La componente x, indichiamola con (grad f )x è data dall’espressione:
(grad f )x =
∂f (x, y, z)
;
∂x
(2.208)
2. La componente y, indichiamola con (grad f )y è data dall’espressione:
(grad f )y =
∂f (x, y, z)
;
∂y
(2.209)
3. La componente z, indichiamola con (grad f )z è data dall’espressione:
(grad f )z =
∂f (x, y, z)
.
∂z
(2.210)
→
−
→
−
→
−
→
Se usiamo la notazione vettoriale, possiamo indicare con −
x = x i +y j +z k
il vettore che rappresenta il punto in cui si valuta la funzione f prima della
→
−
→
−
→
−
→
variazione, con ∆−
x = ∆x i + ∆y j + ∆z k il vettore che rappresenta la
→
−
→
variazione “finita”46 delle coordinate del punto e con il vettore d−
x = dx i +
→
−
→
−
dy j + dz k la variazione infinitesima47 delle coordinate. Quindi la funzione f
→
→
→
viene valutata prima nel punto −
x , poi nel punto −
x + ∆−
x oppure nel punto
→
−
→
−
→
→
x + d x e la variazione della funzione è data dall’espressione f (−
x + ∆−
x)−
→
−
→
−
→
f ( x ), nel caso della variazione finita, oppure dall’espressione df ( x ) = f (−
x +
→
−
→
−
d x ) − f ( x ) nel caso della variazione infinitesima.
Se introduciamo il campo vettoriale definito nella formula (2.207) e se ricordiamo
→
−
→
−
→
→
che il prodotto scalare (−
a · b ) di due vettori −
a e b è espresso dalla formula
−
→
→
(−
a · b ) = ax bx + ay by + az bz
vediamo che possiamo esprimere la formula (2.204) come
f (x + ∆x, y + ∆y, z + ∆z) − f (x, y, z) =
→
= grad f (x, y, z)·∆−
x + errore(∆x, ∆y, ∆z) ;
(2.211)
45 Ricordiamo che un campo vettoriale è una funzione definita in una regione dello spazio i
cui valori, invece di essere numeri sono vettori.
46 La variazione finita è quella per cui non si è ancora stabilito che l’errore è trascurabile e
la variazione della funzione è data dall’approssimazione (2.205).
47 La variazione infinitesima è quella per cui si è stabilito che l’errore è trascurabile e quindi
viene posto uguale a zero per cui la variazione della funzione è data dalla relazione (2.206).
98
la formula (2.205) come
→
f (x + ∆x, y + ∆y, z + ∆z) − f (x, y, z) ≈ grad f (x, y, z)·∆−
x
(2.212)
e la formula (2.206) come
→
df (x, y, z) = grad f (x, y, z)·d−
x .
(2.213)
Assegnata la funzione f , se ne calcoliamo il gradiente, la trasformiamo in
un nuovo oggetto, un campo vettoriale; questa operazione viene anche indicata
dicendo che si applica l’operatore gradiente alla funzione f .
Abbiamo visto una prima proprietà importantissima dell’operatore gradiente: esso permette di calcolare la variazione infinitesima o equivalentemente di
approssimare la variazione finita di una funzione quando si fa variare il punto in
cui si valuta la funzione. A mano a mano che procederemo con lo studio della
fisica, vedremo altre situazioni in cui esso è importantissimo.
2.14.1
La relazione tra l’energia potenziale e il campo di
forze
La prima situazione che incontriamo in cui è importante il gradiente, è la relazione che permette di calcolare un campo di forze conservativo quando ne sia
nota l’energia potenziale.
→→
−
Ricordiamo che se F (−
x ) è un campo di forze conservativo che agisce su un
→
−
punto materiale e U ( x ) ne è l’energia potenziale, il lavoro compiuto dal campo
→
→
sul punto materiale posto in −
x che subisce lo spostamento infinitesimo d−
x è
dato, per definizione di energia potenziale, dall’espressione:
→→ −
−
→
dL = F (−
x )·d→
x = −dU (−
x)
Se confrontiamo questa espressione della variazione infinitesima della funzione U
con l’espressione (2.213) per la variazione infinitesima di una funzione in termini
del gradiente, vediamo che deve valere la relazione:
→ −
−
→
F ·d→
x = − grad U ·d−
x .
Affinché questa identità sia soddisfatta per qualunque spostamento infinitesimo
→
d−
x , deve valere l’importantissima relazione:
→−
−
→
F (→
x ) = − grad U (−
x)
(2.214)
che si scrive per componenti:
→
→
∂U (−
x)
∂U (−
x)
→
→
;
Fy (−
x)=−
;
Fx ( −
x)=−
∂x
∂y
→
∂U (−
x)
→
Fz (−
x)=−
.
∂z
(2.215)
Queste relazioni permettono di calcolare il campo di forze nota che sia l’energia
potenziale; ricordiamo che se invece conosciamo il campo di forze conservativo, se ne calcola l’energia potenziale con l’integrale di linea (2.134) oppure,
equivalentemente, mediante l’integrale della potenza (2.135).
99
2.14.2
La quota ed il suo gradiente; le isoipse
La quota come funzione delle coordinate geografiche
Tutte le considerazioni fatte sopra per le derivate parziali, per il gradiente e
per l’approssimazione di una funzione valgono anche nel caso in cui il numero n
delle variabili sia diverso da tre, purché maggiore di uno (in realtà anche il caso
n = 1 è un caso particolare di quel che è svolto qui).
Per illustrare le proprietà geometriche del gradiente con un esempio concreto,
oltre al caso del campo di forze conservative, per cui il numero delle variabili
vale n = 3, scegliamo un caso in cui il numero n delle variabili vale n = 2.
Consideriamo la topografia di una certa regione: i punti della regione sono
determinati assegnandone le coordinate topografiche, coordinate cartesiane ortogonali che qui chiamiamo x e y; la quota h di un punto della regione è nota,
sulla base della mappa topografica, quando sono note le coordinate x e y del
punto, quindi la mappa rappresenta la quota dei punti della regione come funzione h = h(x, y) delle due variabili x e y. In modo assolutamente equivalente
→
rappresentiamo la funzione h = h(x, y) come funzione h = h(−
x ) della variabile
→
−
→
−
→
−
vettoriale x = x i + y j .
Il gradiente della quota è il vettore
grad h(x, y) =
→ ∂h(x, y) −
→
∂h(x, y) −
i +
j
∂x
∂y
dunque è un vettore che giace nel piano {x, y}, che è il piano della mappa.
Le superfici e le curve di livello
Le superfici di livello di una funzione di n variabili f = F (x1 , x2 , . . . xn ) sono le
superfici sulle quali la funzione è costante, dunque le superfici definite in forma
implicita dalla relazione:
f (x1 , x2 , . . . xn ) = c ,
(2.216)
dove c è una costante; al variare della costante c cambia la superficie di livello.
Nel caso in cui la funzione f sia l’energia potenziale di un campo di forze, o
il potenziale di un campo vettoriale, le superfici di livello si chiamano superfici
equipotenziali . Per esempio, il geoide è una particolare superficie equipotenziale
del campo gravitazionale della Terra, quello osservato, che tiene conto anche del
contributo della forza centrifuga studiato nel § 2.13.6.
Nel caso in cui le variabili siano solo due, le superfici di livello sono più propriamente curve, che chiamiamo curve di livello. In molti casi le curve di livello
hanno nomi specifici. Per esempio, nel caso che consideriamo esplicitamente qui,
→
in cui la funzione h(−
x ) rappresenta la quota dei punti di una regione, le curve
di livello si chiamano isoı̀pse 48 ; nel caso (in realtà identico al precedente) in cui
la funzione f (x, y) rappresenta la profondità (del mare di un lago) si chiamano
isòbate 49 ; se la funzione f rappresenta la misura della pioggia che cade (in un
48 Dal
49 Dal
greco “isos”=uguale e “hypsos”=elevato
greco “isos”=uguale e “batys”=profondo
100
mese, in una stagione, in un anno), le curve di livello si chiamano isoiète 50 ; nel
caso in cui la funzione f (x, y) rappresenta la potenza (spessore) di uno strato
geologico, le curve di livello si chiamano isòpache 51 , e cosı̀ via52 .
Se si rappresentano le curve di livello di una grandezza (potenziale, quota o altro) in una carta, se ne deve fissare il passo, ovvero la differenza di valore della
grandezza tra una curva e l’altra, e dove s’infittiscono la variazione per unità di
lunghezza della grandezza è maggiore. Perciò dove le curve di livello sono fitte,
il gradiente è più grande che non dove sono rade. Per esempio, sappiamo che
dove le isoipse s’infittiscono, la pendenza è forte.
2.14.3
Proprietà geometriche del gradiente
Il gradiente è perpendicolare alle superfici di livello Se un punto si sposta lungo una superficie o curva di livello di una funzione f , per definizione
la variazione della funzione f è nulla e questo vale ovviamente anche nel
caso infinitesimo. In questo caso la variazione è espressa dal prodotto
→
scalare (2.213) del gradiente di f con lo spostamento infinitesimo d−
x del
punto:
→
→
→
df (−
x ) = grad f (−
x )·d−
x .
Come abbiamo detto, questa variazione è nulla se lo spostamento infinite→
simo d−
x giace sulla superficie, o curva, di livello:
→
→
0 = grad f (−
x )·d−
x .
Siccome il prodotto scalare di due vettori nonulli si annulla se e solo se i due
vettori sono ortogonali tra di loro, questa relazione mostra che il vettore
grad f è ortogonale agli spostamenti infinitesimi lungo la superficie o curva
di livello. Dunque il vettore gradiente è sempre diretto perpendicolarmente
alle superfici e alle curve di livello.
• Esempio 2.14.3.1 Un campo di forze conservativo è ovunque diretto
perpendicolarmente alle superfici equipotenziali. Se conosciamo queste
superfici, sappiamo subito che le forze sono perpendicolari ad esse; per
esempio, la forza peso è punto per punto perpendicolare al geoide.
• Esempio 2.14.3.2 Il gradiente della quota di una regione è punto per
punto perpendicolare alle isoipse stesse (ricordiamo che tale vettore
giace nel piano della mappa).
Il gradiente della funzione f ha la direzione di massima variazione
della funzione e il verso di f crescente. Riprendiamo la relazione
50 Dal
greco “isos”=uguale e “hyein”=piovere
“pachys”=spesso (aggettivo, non avverbio)
52 Siccome i nomi specifici di tutte le curve di livello sono parole composte il cui primo
componente è “iso”, che in greco vuol dire uguale, si sta diffondendo il vezzo deprecabile di
chiamare “isocurve” o “isolinee” le curve di livello. Per quel che riguarda me e il corso di
Fisica I, è meglio evitare questo termine
51 Greco
101
(2.213) che esprime la variazione della funzione f mediante il prodotto
→
scalare del gradiente di f con lo spostamento infinitesimo d−
x del punto:
→
→
→
df (−
x ) = grad f (−
x )·d−
x .
→
→
Fissata la lunghezza |d−
x | del vettore d−
x , sappiamo che il prodotto
scalare
→
→
→
→
→
df (−
x ) = grad f (−
x )·d−
x = | grad f (−
x )||d−
x | cos θ
è massimo se l’angolo θ tra i due vettori è nullo. Questo vuol dire che
se si esegue uno spostamento infinitesimo lungo la direzione e il verso del
gradiente, la variazione di f è massima (perché cos θ = 1) ed f cresce,
perché la sua variazione è positiva.
Combiniamo questo punto con il precedente e otteniamo che la direzione
di massima variazione di una funzione è ortogonale alle sue superfici (o
curve) di livello.
2.14.4 Applicazioni: la direzione delle forze, delle linee di massima pendenza, dell’immersione di uno strato
La direzione di massima variazione dell’energia potenziale è la direzione del
campo di forze ed è dunque ortogonale alle superfici equipotenziali. A
causa del segno − nella relazione (2.214) tra la forza e il gradiente dell’energia potenziale, il verso del campo di forze è quello in cui l’energia
potenziale decresce.
La direzione di massima pendenza, massima variazione della quota, è quella del
gradiente, dunque nella carta topografica è quella ortogonale alle isoipse.
Se fosse possibile prescindere dall’attrito, un oggetto scivolerebbe dalla
vetta di una collina seguendo una curva in ogni punto perpendicolare alle
isoipse. Il gradiente indica la direzione della massima pendenza nel verso
della quota crescente, e per questo motivo si chiama “gradiente”, dal latino
“gradior”=salgo.
L’uso della bussola per misurare l’immersione di uno strato. Ricordo che l’immersione di uno strato piano è l’angolo formato tra la direzione del Nord
geografico53 , orientata da Sud a Nord, e la proiezione orizzontale della
direzione della massima pendenza dello strato, orientata dall’alto verso il
basso. L’angolo è misurato in verso orario. La sua misura si basa sul fatto
che le isoipse sono perpendicolari alle linee di massima pendenza, come
descritto qui.
53 Che differisce da quella dell’ago magnetico per la declinazione, il cui valor medio in Italia
è minore di due gradi, quindi minore dell’errore che si può commettere nella misura descritta
qui.
102
Coperchio della bussola, con specchio,
appoggiato allo strato.
S magnetico
L
C
C
180
90
O
270
5
22
5
S
13
W
75
N
30
15
31
45
5
60
Cassa della bussola, orizzontale
0
I
Massima pendenza
verso il basso
Imme
e
rsion
N magnetico
Figura 2.33: L’uso della bussola per la misura dell’immersione. Siccome la
scala della bussola è reciproca (antioraria), si legge direttamente la misura
dell’immersione senza far calcoli. Non ho segnato tutti i gradi della scala.
103
Si appoggia il coperchio, incernierato alla cassa, allo strato e si mette ”in
bolla” la cassa della bussola. Quando la cassa è in bolla è orizzontale e
quindi anche il cardine tra la cassa e il coperchio appoggiato sullo strato è
orizzontale; dunque il cardine è un’isoipsa e la linea di massima pendenza
dello strato gli è ortogonale. La direzione N-S segnata sulla bussola è ortogonale al cardine, quindi rappresenta la proiezione della linea di massima
pendenza sul piano orizzontale della bussola. L’angolo formato tra la direzione N-S e l’ago magnetico, che viene letto cominciando da N della scala
della bussola fino al Nord dell’ago magnetico, coincide con l’immersione,
purché la scala della bussola sia reciproca, cioè misuri gli angoli in verso
antiorario. Nella figura 2.33, si vede che la scala è reciproca, perché è
antioraria, e infatti Ovest (W) è segnato a destra del Nord della bussola.
La linea C-C è il cardine ed è un’isoipsa. La retta I-O-L perpendicolare
alla isoipsa rappresentata dal cardine è la linea di massima pendenza dello strato; essa coincide con la retta N-S della bussola, dove, siccome S è
dalla parte del cardine, N, dunque I, è dalla parte della discesa. L’angolo
\
IO(N
magnetico), il cui valore, 30°, si legge sulla punta del Nord dell’ago
(la metà bianca) è l’angolo misurato in verso antiorario tra la direzione
I-O-L di massima pendenza orientata nel verso della discesa e la direzione
Nord magnetico-Sud magnetico, orientata verso N magnetico. L’ango\
lo IO(N
magnetico) che viene misurato in verso antiorario da I verso N
magnetico, viene misurato, con lo stesso risultato, in verso orario da N
magnetico verso I 54 e dunque è proprio l’immersione.
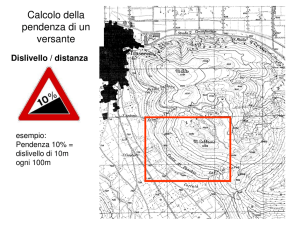
L’uso della carta topografica per il calcolo approssimato della pendenza di un
versante.
Si faccia riferimento alla figura 2.34. Nella figura è rappresentata in modo
ultrasemplificato una carta topografica in cui compaiono solo le isoipse,
scalate di 50 metri in 50 metri, e i punti in cui si vuole stimare la pendenza
del versante, A e C; la scala è 1:s, nel nostro caso vale s= 10 000.
Si procede nel seguente modo.
Stimiamo la pendenza p verso l’alto in A. Si traccia la semiretta in A
perpendicolare all’isoipsa che passa per A (l’isoipsa dei 75 m) e diretta
verso quella immediatamente superiore, dunque verso l’isoipsa dei 100
metri. Questa semiretta incontra l’isoipsa immediatamente superiore in
B. Si misura con un righello la lunghezza l in centimetri del segmento
AB; nel nostro caso vale l = 1, 7 cm. Si trasforma la misura l cm tra i
punti A e B della carta nella distanza55 in metri tra i punti del versante
rappresentati da A e B usando la scala s e passando poi al valore in metri:
L m = (l cm × s) × 10−2 m = (1,7 cm × 104 ) × 10−2 m = 1,7 × 102 m .
54 Detto in altro modo, se N magnetico è a sinistra di I, I è a destra di N magnetico, mentre
l’angolo è lo stesso.
55 Attenzione, questa distanza è misurata sul piano della carta, dunque in orizzontale e non
lungo il pendio.
104
B
150 m
125 m
100 m
A
75 m
50 m
D
C
Figura 2.34: Schema di carta topografica per illustrare l’uso del gradiente per il
calcolo approssimato della pendenza di un versante. Nella “carta topografica”
sono rappresentate solo le isoipse. La scala è 1:10 000.
La differenza di quota ∆h tra l’isoipsa immediatamente superiore rappresentata in carta (100 m) e quella in cui giace il punto A (75 m) vale 25 m.
Finalmente, la pendenza p e la pendenza percentuale p % verso l’alto in A
sono stimate approssimativamente dalle formule:
25
∆h m
=
≈ 0,15 ;
Lm
170
∆h m
p % = p × 100 ≈
× 100 ≈ 0,15 × 100 = 15 % .
Lm
p≈
(2.217)
(2.218)
Se procediamo nello stesso modo nel punto C della mappa, troviamo che
ivi la pendenza percentuale vale p(C) ≈ 63 %. Abbiamo anche ritrovato
il fatto che la pendenza è maggiore dove le isoipse sono più fitte, minore
dove si diradano.
Ora, con l’uso del gradiente, vediamo perché la formula (2.217) dà una
stima, e perché solo approssimata, della pendenza, e quindi perché la formula (2.218) dà una stima approssimata della pendenza percentuale.
Facciamo riferimento alla figura 2.35, che rappresenta la sezione del versante nel piano verticale {s , h} che contiene il punto A e la direzione di
massima pendenza nel punto A; l’ascissa h è la quota, l’asse s è orizzontale, la linea continua v rappresenta l’intersezione del versante con il piano
{s , h} e, ricordiamo, in A rappresenta la direzione di massima variazione
105
della quota. Codesto piano verticale interseca l’isoipsa dei 100 m in B, lo
stesso della figura 2.34.
h
v
h ( s + δ s)
h (x )
B
A
θ
φ
∆h
∆s
s
s + ∆s
s
v
Figura 2.35: Il profilo di un versante e la pendenza. La curva continua v, profilo
del versante, rappresenta l’intersezione del versante con il piano verticale che
passa per i punti A e B della figura 2.34, che è il piano della figura. Codesto
piano contiene la direzione di massima pendenza nel punto A. Si noti che codesto
piano verticale, in generale, non contiene la direzione di massima pendenza negli
altri punti del profilo: per esempio, la direzione di massima pendenza nel punto
B del versante potrebbe non giacere nel piano della figura. Qui la scala non è
rilevante.
La pendenza p in un punto A del versante è definita dal limite del rapporto
incrementale tra la variazione della quota h(s+δs)−h(s) e lo spostamento
δs:
h(s + δs) − h(s)
,
(2.219)
p = lim
δs→0
δs
dove, attenzione, l’asse s orizzontale dev’essere nella direzione della massima pendenza in A.
La determinazione dell’asse s è realizzata dal gradiente: sappiamo che
la direzione della massima pendenza in A è individuata dal gradiente e
quindi sappiamo che è perpendicolare alle isoipse; perciò nella figura 2.34
tracciamo la perpendicolare AB all’isoipsa in A56 . Allora l’asse s è l’asse
orizzontale del piano verticale che passa per AB. Ora conosciamo l’asse
s la cui variabile compare nell’equazione (2.219); a questo punto si tratta
solo di approssimare la derivata in (2.219) mediante un rapporto incrementale che possiamo valutare con i dati a disposizione, e questo rapporto
è:
h(s + ∆s) − h(s)
,
(2.220)
p≈
∆s
56 Si
noti che in generale essa NON è perpendicolare all’isoipsa in B.
106
dove ∆s è la distanza orizzontale tra il punto A e il punto B della figura 2.35 e quindi della figura 2.34. Nella figura vediamo che abbiamo
costruito un’approssimazione, perché questo rapporto incrementale è la
tangente trigonometrica dell’angolo φ della figura 2.35, mentre sappiamo
dal significato geometrico della derivata calcolata in A che la pendenza è
la tangente trigonometrica dell’angolo θ nella stessa figura.
Quindi abbiamo giustificato la costruzione indicata sopra per la pendenza
e visto come mai è approssimata. Se moltiplichiamo per 100 l’approssimazione di p otteniamo l’approssimazione di p %.
OSSERVAZIONE La pendenza non è altro che il modulo del gradiente.
→
→
Infatti vale la relazione tra infinitesimi: dh = grad h·d−
x Se il passo d−
x
ha la direzione della massima pendenza, ha la direzione del gradiente,
→
quindi in questo caso, e solo in questo, vale grad h·d−
x = | grad h|ds, dove
→
−
ds = |d x | se grad x è diretto verso l’alto, mentre se è diretto verso il basso
→
vale ds = −|d−
x |. In conclusione abbiamo la relazione: dh = | grad h|ds
dove la variabile s varia lungo l’asse diretto come grad h, dunque lungo la
linea di massima pendenza; ne segue che vale:
dh
= |gradh| .
ds
107