PLASMONI SUPERFICIALI
Un possibile approccio nello studio delle proprietà fisiche dei metalli
consiste nel considerare gli elettroni liberi presenti all’ interno del loro volume
come un liquido ad alta densità, ignorando, in prima approssimazione, il reticolo.
All’interno di tale liquido possono aver luogo oscillazioni, note come plasmoni di
volume.
Gli elettroni presenti invece sulla superficie del metallo, che sono
normalmente soggetti a fluttuazioni casuali, possono provocare, in presenza di un
opportuno campo elettromagnetico (e sotto certe condizioni), oscillazioni coerenti
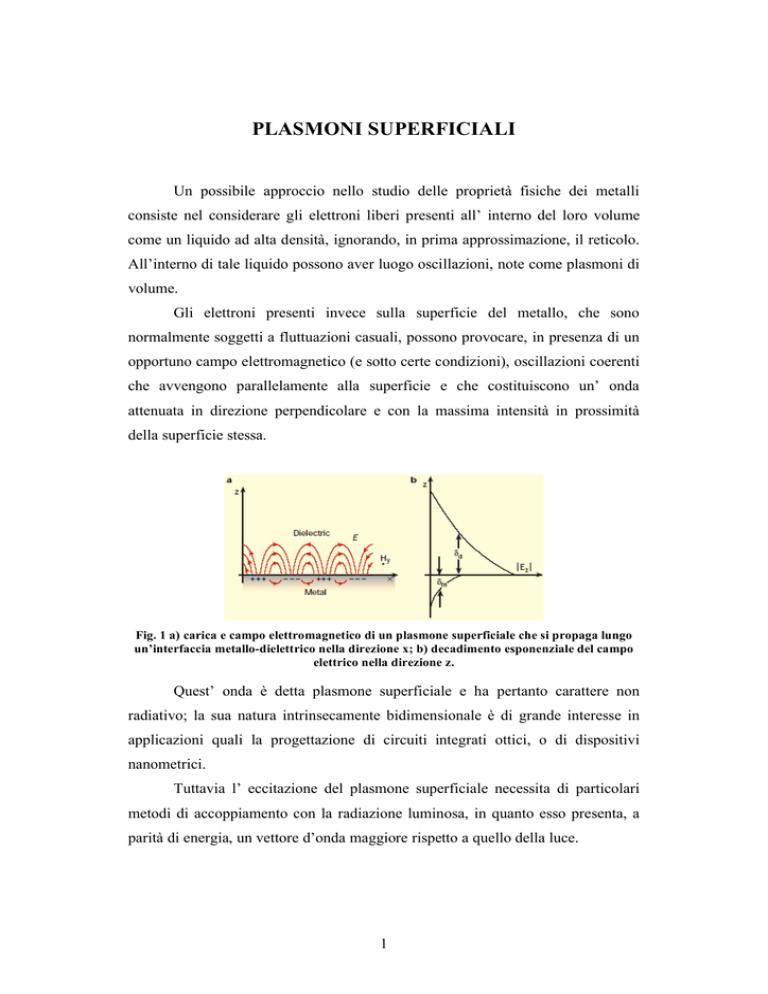
che avvengono parallelamente alla superficie e che costituiscono un’ onda
attenuata in direzione perpendicolare e con la massima intensità in prossimità
della superficie stessa.
Fig. 1 a) carica e campo elettromagnetico di un plasmone superficiale che si propaga lungo
un’interfaccia metallo-dielettrico nella direzione x; b) decadimento esponenziale del campo
elettrico nella direzione z.
Quest’ onda è detta plasmone superficiale e ha pertanto carattere non
radiativo; la sua natura intrinsecamente bidimensionale è di grande interesse in
applicazioni quali la progettazione di circuiti integrati ottici, o di dispositivi
nanometrici.
Tuttavia l’ eccitazione del plasmone superficiale necessita di particolari
metodi di accoppiamento con la radiazione luminosa, in quanto esso presenta, a
parità di energia, un vettore d’onda maggiore rispetto a quello della luce.
1
Ciò equivale a dire che la curva di dispersione del plasmone superficiale, (k),
giace alla destra della curva di dispersione della luce.
Per ricavare tale relazione di dispersione e introdurre alcuni importanti
parametri che caratterizzano i plasmoni di superficie consideriamo un sistema
costituito da un dielettrico isotropo, con costante dielettrica 1 reale e positiva,
occupante il semispazio z > 0, e un metallo, con funzione dielettrica complessa e
dipendente dalla frequenza, ( ) = ' ( ) + i " ( ) , occupante il semispazio z < 0
(fig. 2).
Supponiamo che la struttura in esame sia indefinita nella direzione y, in
modo che il campo elettrico e magnetico risultino indipendenti da tale variabile.
Prendiamo in esame dapprima un’ onda di tipo TM in polarizzazione p,
propagantesi nella direzione x; in tale onda il vettore campo magnetico è
perpendicolare al piano di incidenza (il piano individuato dalla direzione di
propagazione e dalla normale alla superficie, in questo caso il piano x-z).
Ez
z
x
ksp
Hy
1
Ex
()
Fig. 2
Il campo magnetico H e il campo elettrico E possono essere scritti nella
forma:
1
H1(x,z,t) = y0 A eik x x k z z it
E1(x,z,t) = x0 (
1
Ac 1 ik x x k z 1 z it
k Ac
+ z0 ( x ) eik x x k z z it
kz ) e
i 1
1
nel semispazio z > 0 (nel dielettrico), e:
m
Hm(x,z,t) = y0 B e ik x x + k z z it
Em(x,z,t) = x0
m
m
Bc
Bc
k zm e ik x x + k z z it + z0 (
)k x e ik x x + k z z it
i ( )
( )
2
nel semispazio z < 0 (nel metallo).
k 1z e k zm determinano il decadimento del campo elettromagnetico lontano
dall’interfaccia metallo-dielettrico e sono dati da:
k 1z = k x2 1 c
2
k zm = k x2 ( ) c
2
(1)
Le parti reali di k 1z e k zm devono dunque essere positive affinché i campi
descrivano un’ onda superficiale.
Imponiamo ora la continuità delle componenti tangenziali del campo
elettrico e magnetico all’ interfaccia metallo-dielettrico (z = 0).
Dalla condizione E 1x = E xm otteniamo:
Ak 1z
Bk zm
=
1
( )
Mentre dalla condizione H 1y = H ym si ha:
A=B
Otteniamo cioè un sistema omogeneo di due equazioni nelle due incognite A e B,
e affinché esso ammetta soluzioni diverse da quella banale è necessario imporre
che il determinante della matrice dei coefficienti associata sia nullo, condizione
che porta alla relazione di dispersione:
k zm
( )
=
1
1
kz
(2)
3
Se, in un primo momento, assumiamo che ( ) sia reale, k 1z e k zm devono
essere reali e positive affinché le espressioni del campo elettrico e di quello
magnetico descrivano onde che si attenuano al crescere della distanza dalla
superficie di separazione tra i due mezzi. Di conseguenza ( ) deve essere
negativa.
Elevando al quadrato entrambi i membri della relazione di dispersione (2),
e sostituendo le (1), otteniamo un’ espressione esplicita (in funzione di ) per k x ,
che rappresenta il numero d’ onda del plasmone superficiale e che indichiamo
dunque con k sp :
k sp =
1 ( )
c 1 + ( )
(3)
Tale relazione è valida anche se ( ) è complessa. k sp è complesso e, se
assumiamo reale e " ( ) < ' ( ) si ha k sp = k sp '+ik sp " con:
k sp ' =
' ( ) 1
c ' ( ) + 1
3
' ( ) 1 2 " ( )
k sp " = c ' ( ) + 1 2( ' ( )) 2
k sp " determina l’ assorbimento interno, mentre per avere k sp ' reale è necessario
avere ' ( ) < 0 e ' ( ) > 1 ; questa condizione è generalmente soddisfatta nei
metalli al di sotto della frequenza di plasma p, infatti in questo caso si può
scrivere:
p
' ( ) 1 2
4
e dunque ' ( ) < 0 .
Nel seguito si scriverà per comodità k sp al posto di k sp ' .
Dalla relazione di dispersione appena ricavata è dunque evidente il fatto
che il vettore d’ onda del plasmone superficiale sia maggiore, a parità di (e
quindi di energia), di quello della luce nel dielettrico, la cui ampiezza è pari a
1 . Il plasmone superficiale non può pertanto essere trasformato in luce (da
c
qui il suo carattere non radiativo), e non può essere eccitato con la semplice
illuminazione dal dielettrico.
Fig. 3 Curva di dispersione del plasmone superficiale all’interfaccia metallo-dielettrico.
Le perdite ohmiche nel metallo (descritte dalla parte immaginaria di
( ) ), fanno sì che l’ energia trasportata dal PS decada esponenzialmente quando
questo si propaga lungo l’ interfaccia dielettrico-metallo (nella direzione x). La
distanza dopo la quale l’ intensità dei campi diminuisce di
1
del suo valore
e
massimo è detta lunghezza di propagazione (Lsp) ed è legata a k sp " :
5
' ( ) ( ' ( ) 1 )2
3
Lsp =
c
1
=
2k sp " 3
1 2 " ( )
Un altro parametro che è utile introdurre è inoltre la profondità di
penetrazione del campo nel dielettrico e in aria, , che rappresenta la distanza
(lungo z) per la quale l’ intensità dei campi si riduce di
1
del suo valore massimo
e
(assunto in prossimità dell’ interfaccia):
=
1
kz
Nel dielettrico si ha:
d =
2
' ( ) + 1
12
e nel metallo:
m =
' ( ) + 1
.
( ' ( )) 2
Per elevati valori di k sp il campo risulta fortemente concentrato nei pressi
della superficie di separazione tra i due mezzi; per valori di k sp inferiori, il campo
ha nel dielettrico una forte componente traversa E z rispetto a quella longitudinale
E x , e si propaga per lunghe distanze, mentre nel metallo E z si mantiene piccolo
rispetto a E x .
Nelle seguenti tabelle sono riportati, a titolo di esempio, alcuni valori di
d , m e Lsp nel caso in cui il dielettrico sia aria:
6
d
m
ARGENTO
600 nm
390 nm
24 nm
ORO
600 nm
280 nm
31 nm
Lsp
ALLUMINIO
500 nm
2 μm
ARGENTO
500 nm
20 μm
ARGENTO
1.55 μm
1 mm
Consideriamo ora un’ onda TE (in polarizzazione s) che si propaghi nella
struttura di figura 2. Per una tale onda il vettore campo elettrico è perpendicolare
al piano di incidenza (è cioè lungo y).
Eventuali soluzioni di tipo plasmonico per quest’ onda possono essere
scritte come:
1
E(x,z,t) = y0 A e ik x x k z z it
Ack 1z ik x x k 1z z it
Ack x ik x x k 1z z it
H(x,z,t) = x0
+ z0
e
e
i
nel dielettrico (z > 0), e:
m
E(x,z,t) = y0 B e ik x x + k z z it
H(x,z,t) = -x0
Bck zm ik x x + k zm z it
Bck x ik x x + k zm z it
+ z0
e
e
i
nel metallo (z < 0).
Imponendo la continuità delle componenti tangenziali dei campi all’
interfaccia (per z = 0) otteniamo le equazioni:
7
A=B
A
c 1
c
k z = B k zm
i
i
che possono essere combinate nella singola equazione:
(k
1
z
)
+ k zm A = 0
(4)
Poiché le parti reali di k 1z e k zm devono essere entrambe positive per avere
un’ onda superficiale, l’ unica soluzione dell’ equazione (4) è A=0, e quindi B=0,
cioè un campo identicamente nullo.
Dunque un plasmone superficiale in polarizzazione s non può esistere
nella struttura considerata. E’ possibile solo la propagazione di plasmoni
superficiali in polarizzazione p, per eccitare i quali tramite semplice luce incidente
sulla superficie planare del metallo dal mezzo dielettrico adiacente è necessario
che la componente parallela alla superficie del vettore d’ onda della luce,
1
sin (dove è l’ angolo di incidenza), sia uguale al numero d’ onda del
c
1
1 ( ) 2
plasmone, pari a
. Dal momento che, come si è visto dalla
c ( ) + 1 relazione di dispersione, questa condizione non è verificata per la struttura
esaminata, è necessario ricorrere a particolari tecniche, quali ad esempio l’
accoppiamento tramite riflessione totale attenuata (accoppiamento ATR), o
tramite reticoli.
ACCOPPIAMENTO TRAMITE RIFLESSIONE TOTALE ATTENUATA
Un primo esempio di struttura che sfrutta tale metodo è la configurazione
di Kretschmann, costituita da un film metallico posto a contatto con un prisma di
8
vetro da cui proviene l’ onda in polarizzazione p incidente con un angolo maggiore dell’ angolo critico per la riflessione totale.
Fig. 4 Geometria di Kretschmann.
La riflessione totale all’ interfaccia metallo-vetro dà luogo ad un’ onda
evanescente del metallo con velocità di fase pari a v =
c
=
<c
kx
vetro sen
(onda lenta). Tale onda si attenua esponenzialmente in direzione perpendicolare
all’ interfaccia metallo-vetro, ma se il metallo è abbastanza sottile essa non è
completamente nulla quando raggiunge l’ interfaccia metallo-aria e riesce a
eccitare qui il plasmone superficiale nel caso in cui le velocità di fase delle due
onde coincidano:
v sp =
+ ( )
c
c aria
=v=
k sp
aria ( )
vetro sen
(5)
Nella (5) compare il in quanto si è usata l’ espressione di k sp ricavata
precedentemente per la struttura con metallo semiinfinito. In realtà nel caso di un
film metallico di spessore finito l’ interazione tra le due interfacce non può essere
trascurata, e il plasmone che propaga lungo un’ interfaccia “sente” l’ esistenza del
plasmone sull’ altra: ciò fa sì che la relazione di dispersione risulti modificata e si
ottiene un nuovo valore per k sp , pari a k sp0 + k sp , in cui k sp0 è pari al numero d’
onda per la struttura con metallo semiinfinito, e k sp è il termine “correttivo”,
9
complesso: la sua parte reale sposta il valore di k sp0 , mentre la parte immaginaria
inserisce un termine di smorzamento.
Per ricavare la relazione di dispersione esatta per la struttura di
Kretschmann si consideri quindi un sistema costituito da un semispazio vuoto (1
= 1) nella regione z > d, un film metallico, caratterizzato da una funzione
dielettrica () complessa nella regione 0 < z < d, e un dielettrico, con costante
dielettrica s reale e positiva nella regione z < 0 (fig. 5).
z
Ez
Ex
x
Fig. 5
Poichè si vuole studiare un’ onda superficiale TM in polarizzazione p che
propaga nella direzione x, l’ unica componente non nulla del campo magnetico
sarà Hy, e può essere scritta nel modo seguente:
1
Hy(x,z,t) = Ae ik x x k z z it
[
m
m
nel vuoto ( z d );
]
Hy(x,z,t) = e ik x x Be k z z + Ce k z z e it
nel metallo ( 0 z d );
s
Hy(x,z,t) = De ik x x + k z z it
nel dielettrico ( z 0 );
dove:
10
k = k 1 c
1
z
2
2
x
k zs = k x2 s c
2
k = k ( ) c
2
2
x
m
z
Le parti reali di k 1z , k zm e k zs devono essere positive per avere un’ onda
superficiale.
Imponiamo poi le condizioni al contorno per Hy su ciascuna interfaccia; si
deve avere:
-
Hy(x.z.t) continuo;
-
1 H y ( x, z , t )
continuo.
z
Applicando tali condizioni ai campi scritti precedentemente si ottiene un
sistema di equazioni lineari omogenee nelle incognite A, B, C, D. Affinché questo
ammetta soluzioni diverse dalla banale si deve uguagliare a zero il determinante
della matrice dei coefficienti, giungendo così alla relazione di dispersione:
m
( ) k 1z
( ) k zs
( ) k 1z
( ) k zs
+
+
=
1 e 2 k z d
1
1
1
m
m
m
m
1 k z
s k z
1 k z
s k z
Nel limite in cui d si ha:
( ) k 1z
+1 = 0
1 k zm
( ) k zs
+1 = 0
s k zm
11
(6)
Si riottengono cioè le relazioni di dispersione analoghe alla (2) per il plasmone
superficiale all’ interfaccia metallo-aria e metallo-dielettrico.
Dalla relazione (6) si può ottenere l’ espressione di k sp in funzione della
frequenza; la condizione per l’ accoppiamento luce-plasmone è sempre:
k sp =
s sen
c
(7)
Sotto questa condizione di risonanza si osserva un minimo accentuato
nella riflettività all’ interfaccia dielettrico-metallo, che corrisponde all’
eccitazione del plasmone all’ altra interfaccia. Questo minimo può essere nullo
per un certo valore di d, dipendente a sua volta da ( ) , mentre sparisce per
d .
Fig. 6 Andamento della riflettività in funzione dell’ angolo di incidenza per vari spessori d
del film metallico (Ag).
All’ interfaccia metallo-dielettrico invece il PS non può essere eccitato
perché il suo vettore d’ onda è ancora maggiore di quello della luce incidente per
ogni valore dell’ angolo .
12
Fig. 7 Curve di dispersione del plasmone superficiale alle interfacce di un film d’argento
(d=30nm) su substrato dielettrico ( s=2.25) in aria.
Un’ altra struttura che sfrutta l’ accoppiamento ATR è la configurazione di
Otto, adatta per metalli di spessore più elevato. In questo caso la superficie
metallica, caratterizzata da funzione dielettrica
( ) è separata dal prisma
dielettrico (con costante dielettrica s ) da una gap di aria di spessore h. Il campo
incidente in polarizzazione p proviene dal prisma e l’ angolo di incidenza è
maggiore dell’ angolo critico all’ interfaccia prisma-aria. Anche qui l’ onda
evanescente che viene eccitata in aria decade esponenzialmente verso il metallo,
ma se la gap è abbastanza stretta essa non svanisce completamente all’ interfaccia
aria-metallo ed eccita qui il plasmone superficiale.
Fig. 8 Configurazione di Otto.
13
La condizione di risonanza è analoga a quella ottenuta per la configurazione di
Kretschmann.
La larghezza della gap può essere dimensionata osservando l’ andamento
della riflettività nel prisma al variare di h per un angolo di incidenza fissato.
Fig. 9 Andamento dei coefficienti di riflessione d’ampiezza per la polarizzazione s e p in
funzione della larghezza della gap per diversi valori dell’angolo di incidenza .
ACCOPPIAMENTO TRAMITE RETICOLI DIFFRATTIVI
Un’ alternativa all’ eccitazione di plasmoni superficiali tramite
accoppiamento ATR sfrutta reticoli diffrattivi; se infatti la luce proveniente da un
mezzo dielettrico colpisce un reticolo metallico si osservano delle anomalie dello
spettro di riflessione. Tale fenomeno fu osservato per la prima volta da Wood, il
quale fu il primo a suggerire che esse potessero essere dovute all’ eccitazione di
onde superficiali, i plasmoni appunto.
Si consideri dunque una superficie metallica posta sul piano x-y, sulla
quale si abbia una modulazione periodica di periodo a, e sulla quale incida un
fascio di luce con un angolo 0 .
14
Fig. 10 Eccitazione di plasmoni superficiali tramite diffrazione su un reticolo.
Le componenti della luce diffratta il cui vettore d’ onda coincide con k sp
potranno eccitare il plasmone superficiale lungo la superficie del reticolo. Si deve
cioè avere:
kx =
sen 0 ± g = k sp
c
Dove è un intero e g =
2
.
a
Più in generale, nel caso di una generica perturbazione della superficie
metallica, si può scrivere:
kx =
sen 0 ± k x = k sp
c
dove k x tiene conto della variazione di k x introdotta dalla modulazione della
superficie liscia del metallo, e per k x =0 non si hanno soluzioni per la relazione
di dispersione.
Il fenomeno inverso è anch’ esso possibile: un PS che si propaghi
attraverso il reticolo (o più in generale attraverso una superficie corrugata) può
ridurre, proprio a causa della perturbazione, il suo vettore d’ onda di un k x in
modo da trasformarsi in luce.
15
EFFETTI DI LOCALIZZAZIONE DEL CAMPO
Se la perturbazione della superficie del metallo è sufficientemente
profonda i plasmoni superficiali vengono fortemente scatterati e si comportano in
modo disordinato di modo che la loro propagazione attraverso la superficie
assomiglia ad un processo di diffusione. Ciò provoca degli accumuli localizzati di
densità di campo elettromagnetico più elevati di quelli causati da un plasmone
superficiale che propaga su una superficie liscia o con perturbazione ridotta. Si
ottengono cioè delle eccitazioni superficiali confinate che prendono il nome di
plasmoni superficiali localizzati e che si sviluppano grazie all’ accentuata
modulazione del metallo, oppure possono aver luogo in particolari strutture dalla
geometria confinata, quali ad esempio particelle metalliche immerse nel
dielettrico. La relazione di dispersione per queste onde può essere ricavata nell’
approssimazione elettrostatica, risolvendo l’ equazione di Laplace con le relative
condizioni al contorno. Ciò ha senso se la dimensione caratteristica a del sistema
considerato è piccola rispetto alla lunghezza d’ onda del plasmone superficiale
localizzato ( a << ).
A titolo di esempio, si consideri una sfera metallica di raggio R, centrata
nell’ origine, e immersa in un mezzo di costante dielettrica 0 (fig. 11).
0
R
Fig. 11
Il potenziale elettrostatico (r , , ) all’ interno della sfera può essere
scritto come:
16
in (r , , ) = a
=0 m = m
r Ym ( , )
0rR
dove Ym ( , ) è un’ armonica sferica.
Similmente all’ esterno della sfera si ha:
out (r , , ) = b
=0 m = m
1
r +1
Ym ( , )
rR
Imponendo le condizioni al contorno sulla superficie della sfera, cioè la
continuità di (r , , ) e di si ottiene dunque la relazione di dispersione per
r
il plasmone localizzato:
( ) + 1
+
=0
0
E’ opportuno sottolineare che i plasmoni localizzati (anche detti risonanze
superficiali) sono eccitazioni notevolmente diverse dai plasmoni superficiali
propaganti; essi sono confinati in strutture metalliche curve e sono caratterizzati
da frequenza discreta e complessa dipendente dalla dimensione e dalla forma dell’
oggetto in cui si sviluppano. Possono essere inoltre eccitati per mezzo di luce di
adeguata frequenza e polarizzazione, indipendentemente dal vettore d’ onda di
tale luce. I plasmoni superficiali propaganti invece possono essere eccitati se sia la
frequenza che il vettore d’ onda della luce incidente sono appropriati.
I due tipi di eccitazioni possono presentarsi sovrapposti oppure
separatamente, come si vedrà in seguito.
A tale proposito si consideri una struttura, nella quale i due effetti si
manifestano separatamente, costituita da un reticolo metallico nel quale si
vogliono studiare gli effetti risonanti legati all’ eccitazione di plasmoni localizzati.
17
Supponiamo che il semispazio per z > 0 (regione 1) sia riempito da un
dielettrico privo di perdite di costante dielettrica 1 , mentre per z < 0 (regione 2)
si ha un metallo con funzione dielettrica 2 ( ) . Per z = 0 la superficie del metallo
è modulata secondo la funzione z = f(x), periodica in x con periodo g (fig. 12).
z
Regione 1
1
z = f(x)
x
Regione 2
2()
Fig. 12
Dal dielettrico proviene un’ onda TM di lunghezza d’ onda 0 e frequenza
che incide normalmente sul reticolo. Il campo incidente può allora essere
espresso nella seguente forma:
Ei(x,z,t) = x0 E xi e i ( k0
1 z + t )
Hi(x,z,t) = y0 H yi e i ( k0
1 z + t )
dove k 0 =
+ z0 E zi e i ( k0
1 z + t )
2
è il modulo del vettore d’ onda nello spazio libero. Il campo
0
riflesso (per z > max f(x)) e quello trasmesso (per z < min f(x)) possono essere
scritti come sovrapposizione di onde diffratte:
Er(x,z,t) =
N = Hr(x,z,t) =
N = (x0 E 1xN + z0 E 1zN ) e [i ( N x + N z t )]
1
1
y0 H 1yN e [i ( N x + N z t )]
18
Et(x,z,t) =
M = Ht(x,z,t) =
M = 2
2
(x0 E xM
+ z0 E zM
) e [i ( M x M z t )]
2
2
2
y0 H yM
e [i ( M x M z t )]
in cui N = NK g (con N intero e K g =
2
) e Ni = i k 02 N2 (i = 1,2) sono le
g
componenti del vettore d’ onda del N-esimo ordine diffratto nelle direzioni x e z,
rispettivamente.
E’ necessario ora imporre le condizioni di continuità sulla superficie di
separazione metallo-dielettrico, e per fare ciò conviene introdurre una
trasformazione di coordinate (x, y, z ) (u , v, w) che porti l’ interfaccia z = f(x)
nella superficie piatta v = z - f(x) = 0.
Imponendo le condizioni, è possibile ricavare (con passaggi che qui non
riportiamo) il campo elettrico e quello magnetico totali all’ interno delle
scanalature del reticolo e la riflettività totale.
Se la modulazione della superficie metallica è del seguente tipo:
z = f ( x) = a 2 7 1
2Nx
g 2 cos
N =1 N
g
(dove lo sviluppo è stato arrestato al settimo termine per semplicità di calcolo e
variando a è possibile variare la profondità delle scanalature del reticolo), e il
metallo è argento ( 2 = 6.5329 + 0.7373i ) l’ andamento della riflettività Rp in
funzione della profondità delle scanalature del grating dg è quello riportato in
figura 13 per due valori del periodo, g =30nm e g =100nm e per radiazione
incidente di lunghezza d’ onda pari a 0 =459.3nm.
19
Fig. 13 Riflettività in funzione della profondità dg delle scanalature per la struttura di fig. 12.
Le curve presentano una serie di minimi per quelle dg per le quali l’ onda
incidente eccita il plasmone superficiale localizzato, cioè per quei valori di dg per
cui le cavità costituite dalle scanalature del reticolo diventano risonanti, e al loro
interno si eccita un’ onda stazionaria con (m-1) nodi nella cavità nel caso della
risonanza m-esima. La differenza (d gm d gm 1 ) tra due valori risonanti successivi
di dg è pari a metà della lunghezza d’ onda del plasmone nella cavità e si ha che
per g più bassi la parte reale della componente z del vettore d’ onda del
plasmone è maggiore.
La figura 14 mostra invece la distribuzione del modulo del campo
magnetico totale |Htot(x,z)|=|Hy(x,z)| all’ interno di un periodo del reticolo in
funzione di x e z per g =100 nm alla terza risonanza.
20
z (nm)
|Hy(x,z)|
Fig. 14
Sono presenti due nodi nel dielettrico nella cavità, come ci si aspetta per la
terza risonanza. La riflettività è Rp=0.3838 e nelle zone più scure vi è un aumento
del campo di un fattore 4.
La figura 15 mostra invece la corrispondente distribuzione di |Etot(x,z)|. Il
campo, come ci si aspetta, assume il suo valore massimo sul fondo della cavità,
dove è presente un aumento di un fattore 26.
z (nm)
|Etot(x,z)|
Fig. 15
21
Dall’ analisi della struttura appena considerata è dunque evidente il ruolo
giocato
dai
plasmoni
localizzati
nella
concentrazione
dell’
energia
elettromagnetica all’ interno delle scanalature, con conseguente aumento locale
dell’ intensità del campo, e nell’ assorbimento di radiazione polarizzata con il
campo H nella direzione delle scanalature. Tale assorbimento avviene per un
vasto range di angoli di incidenza, in quanto i plasmoni localizzati presentano
curve di dispersione piatte.
Consideriamo ora un’ altra struttura periodica in cui sia possibile l’
eccitazione di plasmoni superficiali di entrambi i tipi; in particolare, studiando le
curve di dispersione si vedrà che in tale struttura le due eccitazioni compaiono
sovrapposte, dando origine a modi ibridi.
Il sistema è costituito da un reticolo metallico riflettente con una
perturbazione periodica di tipo “onda quadra”. Le scanalature hanno una
larghezza a, una profondità h e il periodo è d.
La regione di spazio per z > 0 (regione 1) è riempita d’ aria, mentre per z <
0 abbiamo il reticolo, che supponiamo in oro.
Fig. 16
Sul reticolo incide luce in polarizzazione p (con H parallelo alle
scanalature), con angolo di incidenza .
Per analizzare le proprietà di tale sistema facciamo due approssimazioni:
22
-
imponiamo
condizioni
di
impedenza
superficiale
sulle
superfici
metalliche, fatta eccezione per le pareti verticali delle scanalature, che
assumiamo perfettamente conduttrici;
-
poiché la lunghezza d’ onda della luce incidente sul reticolo è molto
maggiore di a, nell’ espansione modale dei campi all’ interno delle
scanalature consideriamo solo il modo fondamentale.
Con queste ipotesi si può scrivere la componente lungo y del campo
magnetico nella regione 1 (z > 0) come sovrapposizione di onde piane ed
evanescenti (trascurando la dipendenza dal tempo):
H 1y ( x, z ) = e ik0 (xsen z cos ) +
rn e
ik 0 n x + 1 n2 z n = n in cui rn è l’ ampiezza dell’ n-esimo ordine diffratto e n = sen + .
d Nella regione 2 l’ ampiezza del modo fondamentale all’ interno delle
scanalature è data da:
1 02 e ik0 h
a
A0 =
1+
sin c k 0 0 2 Dsenk 0 h 2
1 02 + con =
1
metallo
.
Il denominatore di A0 può essere espresso nella forma seguente:
a sin c k 0 n 2 cot (k 0 h ) i
ia
D=
(1 + ) 1 d n = 1 n2 + 23
2
e poichè gli zeri della sua parte reale governano il comportamento della riflettività
della struttura, dalla sua analisi è possibile studiare l’ eccitazione dei plasmoni
superficiali; in particolare si può ottenere la curva di dispersione (k x ) .
Si consideri dapprima il caso in cui si abbia d = 3.5 μm, a = 0.5 μm e h =
0.6 μm. Nella figura 17 è mostrato il diagramma di dispersione relativo e, per
confronto, anche la curva per h 0 , caso in cui sono eccitati solo plasmoni
superficiali che si propagano.
Fig. 17
La presenza delle scanalature introduce una gap tra la prima e la seconda
banda, all’ interno della quale compare un nuovo modo. La relativa curva è
abbastanza piatta, mostra cioè una piccola dispersione rispetto a kx, ed è legata ad
un plasmone superficiale localizzato. Il campo elettromagnetico è fortemente
concentrato nelle scanalature, come ci si aspetta per un fenomeno risonante.
L’ andamento del coefficiente di riflessione in funzione dell’ energia dell’
onda piana in polarizzazione p incidente con un angolo pari a 21° è mostrato
invece nella figura 18:
24
Fig. 18
La linea tratteggiata è stata ottenuta con il metodo dell’ espansione
modale, quella a puntini con il metodo della matrice di trasferimento e quella
continua deriva dal risultato sperimentale.
Il primo minimo, per E 0.25eV corrisponde ad un modo nella prima
banda, e dovrebbe perciò avere carattere propagante; in realtà esso presenta invece
un carattere ibrido, combinazione di un plasmone propagante e localizzato. Il
campo ha infatti picchi di intensità molto elevati agli angoli superiori delle
scanalature, dove è circa 300 volte maggiore dell’ intensità della luce incidente.
Il minimo più pronunciato, per E 0.37eV è invece associato al plasmone
localizzato (linea piatta tra la prima e la seconda banda); in questo caso il campo
elettrico è concentrato principalmente all’ interno della cavità, dove arriva ad
essere 100 volte maggiore del campo incidente, ed è praticamente zero nelle altre
regioni.
Se si considera ora una struttura analoga alla precedente, ma con
scanalature molto strette e profonde (in particolare si ponga d = 1.75 μm, a = 0.3
μm e h = 1 μm), si ottiene il seguente diagramma di dispersione:
25
Fig. 19
In questo caso il modo a energia minore è un plasmone localizzato, con
curva di dispersione molto piatta per E 0.266eV . Al variare dell’ angolo di
incidenza dunque l’ energia di tale modo rimane pressoché inalterata.
La seconda e la terza banda corrispondono a energie maggiori e sono
estremamente vicine per incidenza normale. Il ramo inferiore E 0.693eV ha
ancora carattere ibrido, il campo è concentrato sia nelle scanalature che sulla
superficie metallica orizzontale e raggiunge intensità fino a 400 volte maggiori
della luce incidente.
Nelle figure seguenti si può osservare il campo elettrico nella struttura per
E 0.266eV
(fig. 20), corrispondente al plasmone localizzato, e per
E 0.693eV (fig. 21), corrispondente al modo ibrido, per incidenza normale.
Nel caso del plasmone localizzato (fig. 20) solo le pareti verticali delle
cavità hanno un ruolo attivo nel processo di scattering: la luce incidente induce un
dipolo alternante su di esse a causa della vicinanza delle due superfici.
26
Fig. 20
Il campo elettrico è notevolmente amplificato nelle scanalature, e il valore
di questo incremento è legato al rapporto
a
: quando la lunghezza d’ onda della
d
luce è maggiore del periodo del reticolo ( > d ) e molto maggiore della larghezza
delle scanalature ( >> a ) la parte immaginaria del denominatore D, alla
frequenza per la quale la parte reale di D è nulla, è proprio
a
(assumendo pareti
d
perfettamente conduttrici = 0 ). Dunque si ha:
d e ik0 h
A0 =
a senk 0 h
(8)
Poiché la condizione di risonanza nella cavità prevede cos k 0 h =0, ne
deriva che senk 0 h = 1 , dunque l’ incremento dell’ intensità del campo all’ interno
2
d delle scanalature è volte l’ intensità del campo incidente. E’ quindi evidente
a
come, dimensionando adeguatamente la struttura, sia possibile ottenere campi
elettrici localmente molto elevati.
Nel caso del modo ibrido (fig. 21) per E 0.693eV il campo elettrico è
distribuito sia sulle superfici metalliche orizzontali che all’ interno delle cavità, ed
è molto elevato agli angoli superiori di queste.
27
Fig. 21
La relazione (8) per A0 continua a essere valida, ma in questo caso, poiché
abbiamo un modo ibrido e non una pura risonanza, senk 0 h 1 , dunque A0 può
essere estremamente elevato. Ciò spiega le grandi intensità di campo raggiunte da
questi modi.
APPLICAZIONI
RETICOLI DI TRASMISSIONE
La sempre maggiore miniaturizzazione dei dispositivi negli ultimi anni ha
focalizzato l’ attenzione sulla capacità dei fenomeni plasmonici di propagarsi in
strutture di dimensioni minori della lunghezza d’ onda.
In particolare è di grande interesse per lo sviluppo di dispositivi
nanofotonici lo studio del ruolo dei plasmoni superficiali nell’ elevata
trasmissione ottica osservata attraverso reticoli trasmissivi di dimensioni inferiori
a . In questi ultimi è possibile infatti osservare, per alcune lunghezze d’ onda
della luce incidente, un’ efficienza di trasmissione molto maggiore di quella
attesa, in alcuni casi prossima al 100%. Questo incremento è dovuto a meccanismi
28
direttamente collegati con l’ eccitazione di plasmoni superficiali sulle due
superfici del reticolo.
A tale proposito prendiamo in considerazione una struttura reticolare
metallica bidimensionale per la quale vogliamo studiare il comportamento della
trasmittanza al variare della funzione dielettrica del metallo; in particolare, poiché
sappiamo che, affinché di abbia eccitazione di plasmoni superficiali, è necessario
che la parte reale della funzione dielettrica sia negativa, si può vedere che per
metalli che non verificano tale condizione, come il tungsteno, e quindi non
supportano plasmoni superficiali, la trasmittanza è notevolmente ridotta.
La struttura considerata (fig. 22) è composta da un substrato di vetro su cui
è depositato un array metallico di 400 fori spesso 250 nm. Il periodo P varia da
200 nm a 500 nm e il diametro dei fori d è tale che il rapporto
P
= cos t = 1.75 .
d
Fig. 22 Immagine realizzata mediante microscopio a scansione elettronica (SEM) dell’array
metallico per diversi valori del periodo P.
L’ andamento dell’ intensità trasmessa per vari metalli e per incidenza
normale in funzione della lunghezza d’ onda è riportato in figura 23 e mostra una
serie di picchi corrispondenti all’ eccitazione di plasmoni superficiali sulle due
interfacce, aria-metallo e metallo-vetro.
29
Fig. 23
Esaminiamo dunque il picco corrispondente all’ energia più bassa
( maggiore), indicato nella figura 23 dalla freccia. Questo picco è associato il
modo (1,0) nel substrato di vetro ed è sufficientemente isolato dagli altri in modo
da poter essere studiato senza difficoltà. La posizione spettrale del picco (figura
24) varia con il periodo e si sposta verso lunghezze d’ onda maggiori al crescere
di quest’ ultimo; per P grandi le curve tendono asintoticamente alla linea di
dispersione del plasmone, mentre per piccoli valori di P le curve dei metalli nobili
divergono verso valori definiti delle particolari proprietà ottiche del metallo. Il
tungsteno presenta invece un’ andamento lineare.
30
Fig. 24 Posizione del picco per diversi metalli in funzione del periodo dell’array.
L’ intensità di trasmissione normalizzata, mostrata in figura 25-a) in
funzione della posizione spettrale del picco, è notevolmente diversa per i metalli
nobili e di transizione. Per i primi si nota che essa cresce quando il picco si sposta
verso lunghezze d’ onda maggiori; ciò può essere spiegato considerando che allo
stesso tempo aumenta anche il valore assoluto della parte reale di m (funzione
dielettrica del metallo), il cui andamento è mostrato in figura 25-b), anche se in
realtà il meccanismo è più complicato; bisogna infatti considerare l’ attenuazione
all’ interno di ogni buco, che si comporta come una guida d’ onda cilindrica di
raggio r =
d
in cui si propaga un modo sotto cut-off. Al crescere di tale
2
attenuazione diminuisce e la trasmissione aumenta. A ciò bisogna aggiungere che
il raggio effettivo dei buchi è in realtà maggiore di r a causa della profondità di
penetrazione finita del metallo (a sua volta dipendente dalla funzione dielettrica).
31
a)
b)
Fig. 25
I metalli di transizione presentano invece un’ intensità di trasmissione
estremamente bassa. Per il Co e il Ni ciò è dovuto all’ elevato valore della parte
immaginaria della costante dielettrica che provoca uno smorzamento. Nel caso del
tungsteno invece la bassa trasmissione è da attribuire al fatto che la funzione
dielettrica nel range di frequenze considerato ha parte reale positiva e di
conseguenza esso non può supportare plasmoni superficiali. Il fenomeno di
trasmissione è pertanto puramente diffrattivo ed estremamente debole .
Per comprendere il ruolo fisico giocato dai plasmoni nel processo di
trasmissione consideriamo ora per semplicità una struttura unidimensionale
costituita da un reticolo metallico, su cui siano state praticate delle fessure
longitudinali molto sottili, posto su un substrato dielettrico. Il metallo è l’ oro, il
periodo del reticolo è d, le fessure hanno larghezza a e profondità h (fig. 26). Su
tale sistema incide normalmente radiazione in polarizzazione p. Assumiamo
inoltre a << d e la frequenza della luce incidente al di sotto della frequenza di
plasma del metallo.
32
Fig. 26
Siamo interessati all’ andamento della trasmittanza di ordine zero del
reticolo in funzione di . Questa è riportata nella figura seguente per vari valori di
h, per d = 3.5μm , a = 0.5μm e nel caso in cui il sistema sia nel vuoto.
Fig. 27
Per fessure abbastanza profonde ( h 0.6 μm ) si osserva un picco
pronunciato in corrispondenza di lunghezze d’ onda poco più grandi del periodo.
Tale picco si sposta verso lunghezze d’ onda maggiori e si allarga al crescere di h.
33
Quando h diviene sufficientemente grande ( h 2 μm ) si osservano inoltre anche
altri picchi per successive .
L’ origine fisica di questi picchi di trasmissione può essere studiata
osservando a curva di dispersione (k x ) , mostrata in figura 28 per h = 0.6 μm .
Fig. 28
Il ramo più in basso è associato a un modo di natura plasmonica che
propaga su ogni faccia del reticolo con E 0.348eV per kx=0. La sua posizione
spettrale corrisponde al primo picco di trasmissione, per d e in questo caso si
parla di plasmoni superficiali accoppiati.
Aumentando h nel diagramma di dispersione (fig. 29) compaiono, come
nel caso del reticolo riflettente, nuove bande, corrispondenti all’ eccitazione di
plasmoni localizzati. Per h = 3μm è presente una banda piatta per E = 0.17eV ,
dovuta a un plasmone localizzato associato al picco di trasmissione a = 7.5μm ,
mentre il picco a 4 μm è legato al ramo inferiore della banda dopo la prima
gap.
34
Fig. 29
Si può dunque dedurre che i meccanismi che concorrono alla formazione
dei picchi di trasmissione sono due: i plasmoni accoppiati sono responsabili del
picco per d , mentre i plasmoni localizzati del picco per >> d . Nel primo
caso, a differenza del secondo, la banda non è molto piatta, dunque vi è una forte
dipendenza dall’ angolo di incidenza .
Il processo di trasmissione avviene nel modo seguente: la luce incidente
eccita il plasmone sulla superficie superiore del reticolo; tale modo si accoppia
attraverso le fessure con il plasmone sulla superficie sottostante e questo eccita a
sua volta radiazione luminosa della stessa frequenza e con lo stesso momento di
quella incidente. Questo meccanismo è molto sensibile alla presenza del substrato
sulla superficie inferiore, e se le energie dei due plasmoni coinvolti non
coincidono l’ accoppiamento è meno efficace; inoltre, da un’ analisi della
trasmittanza al variare di a, sarebbe possibile vedere che è necessario un valore
minimo della larghezza delle fessure per accoppiare i plasmoni sulle due superfici
del reticolo.
Il meccanismo di trasmissione associato ai plasmoni localizzati è invece
molto diverso: il campo incidente induce densità di corrente sulle pareti delle
35
fessure, con segno opposto su ogni lato. Il processo non è molto sensibile all’
indice di rifrazione del substrato. Il campo localizzato nelle fessure riesce poi a
riemettere radiazione dal lato opposto del reticolo con alta efficienza.
Le configurazioni di campo nei due casi sono mostrate in figura 30:
Fig. 30 Configurazione di campo elettrico per due periodi del reticolo di trasmissione nei casi
h=0.6μ m (in alto) e h=3μ m (in basso) nel vuoto.
Le straordinarie proprietà trasmissive dei reticoli metallici come quello
appena descritto possono avere importanti applicazioni pratiche: la posizione
spettrale dei picchi di trasmissione e la loro larghezza possono infatti essere
36
controllate variando fattori geometrici, e ciò consente ad esempio di ottenere filtri
per la radiazione elettromagnetica senza effetti diffrattivi.
CIRCUITI PLASMONICI
L’ idea di circuiti basati sui plasmoni superficiali è legata al problema
della miniaturizzazione dei circuiti elettronici, che, se da un lato ha portato a
componenti con prestazioni sempre migliori, dall’ altro è stata accompagnata da
un peggioramento dal punto di vista delle interconnessioni, i cui ritardi limitano la
velocità dei circuiti digitali.
La fotonica offre una parziale soluzione al problema implementando
sistemi basati su fibre ottiche, che non sono però integrabili, in quanto le loro
dimensioni sono molto maggiori di quelle dei circuiti elettronici, inferiori ai 100
nm. Un ulteriore problema è dato dalla diffrazione ottica, dal momento che le
lunghezze d’ onda utilizzate nei circuiti fotonici sono dell’ ordine dei 1000 nm. I
plasmoni superficiali offrono l’ opportunità di confinare la luce in dimensioni
minori di , e consentono di progettare circuiti in cui i segnali elettronici vengono
convertiti in plasmoni superficiali che propagano e vengono processati dagli
elementi ottici, per poi essere riconvertiti in segnali elettronici.
Un primo problema da affrontare riguarda dunque le tecniche per guidare i
plasmoni in strutture metalliche di dimensioni inferiori alla lunghezza d’ onda.
Una possibile sistema è costituito da un sottile film metallico di larghezza
finita immerso nel dielettrico (figura 31); tale geometria offre buoni risultati in
termini di lunghezza di propagazione (circa 13.6 mm per una lunghezza d’ onda di
1550 nm), ma non in termini di confinamento del campo nelle due direzioni
trasverse (x e y), lungo le quali si ha una propagazione non desiderata su distanze
maggiori di .
37
z
r
y
Fig. 31
Riducendo lo spessore del film fino a ottenere un filo nanometrico si riesce
invece a ottenere un’ attenuazione del campo entro distanze minori di lungo x e
y, ma in questo caso le perdite associate al riscaldamento del metallo limitano
fortemente la massima lunghezza di propagazione (lungo z) ottenibile.
Per evitare le perdite ohmiche è possibile ricorrere a un array di
nanoparticelle metalliche circondate da dielettrico che consentono di guidare il
plasmone e allo stesso tempo di limitare le perdite grazie al ridotto volume del
metallo.
In figura 32 è mostrato un esempio di tale guida in cui particelle d’ oro
sono poste su un wafer di silicio-isolante e la lunghezza d’ onda di lavoro è di
1500 nm.
Fig. 32 Campo elettrico (A) ottenuto tramite simulazione FDTD all’interno della guida (B).
La struttura della guida non è uniforme lungo y, in quanto la dimensione
delle particelle metalliche è ridotta da 80nm 80nm al centro fino a 50nm 50nm
38
ai bordi della guida. Ciò permette di concentrare maggiormente il campo al
centro, anche se in realtà tale effetto è limitato sostanzialmente solo alla direzione
x, mentre lungo y si ha un’ estensione dell’ ordine di .
Un metodo per ottenere confinamento in entrambe le direzioni trasverse è
quello di guidare i plasmoni in scanalature metalliche a forma di V (figura 33). In
questo modo si riesce a combinare una forte localizzazione trasversa con una
propagazione unimodale, possibilità di trasmissione del 100% nei tratti curvie alta
tolleranza a imperfezioni strutturali.
x
y
Fig. 33
Per guidare il campo è necessario che l’ angolo sia minore dell’ angolo
critico, e in questo caso si ottengono valori soddisfacenti anche per la lunghezza
di propagazione.
Ad esempio, per una struttura con scanalature larghe 0.6 μm e profonde
1μm (
17° ), nel caso in cui il metallo sia oro, si ottiene una lunghezza di
2
propagazione tra i 90 μm e i 250 μm .
Un punto molto importante nella progettazione di chip plasmonici, è la
conversione di segnali ottici provenienti da dispositivi fotonici in plasmoni
superficiali. Questo processo necessita di accoppiatori che devono presentare alta
efficienza di conversione. Una possibile soluzione prevede la combinazione di
particelle metalliche semisferiche che facciano da focalizzatore plasmonico e di
una guida a nanoparticelle. Nella figura 34 è mostrato un esempio in cui 19
particelle disposte lungo un semicerchio del raggio di 5μm convertono la luce
incidente (che ha una lunghezza d’ onda di 532 nm ed è in polarizzazione p) nel
plasmone e lo focalizzano in una zona ad elevata intensità di campo dove questo
39
si accoppia con una guida metallica. Il campo si propaga nella guida e penetra
parzialmente nella biforcazione finale, larga 100 nm e dunque di dimensioni
inferiori a .
Fig. 34 Immagine ottenuta al SEM dell’ array focalizzante di nanoparticelle metalliche
accoppiato con una guida in Ag di larghezza 250nm.
Sono possibili altre configurazioni, ma la combinazione di array
focalizzanti e di guide nanometriche è, per ora, un elemento fondamentale nel
progetto di circuiti planari plasmonici.
Infine sono ovviamente necessari elementi che consentano il controllo
attivo dei segnali, che costituiscono uno degli obiettivi dell’ attuale ricerca nel
campo della plasmonica.
SORGENTI LUMINOSE
Le possibili applicazioni dei plasmoni superficiali non sono limitate alla
sola progettazione di strutture nanometriche; essi possono infatti essere utilizzati
per risolvere il problema della bassa efficienza nei diodi ad emissione di luce
(LED). In tali dispositivi la produzione di radiazione luminosa prevede l’
iniezione di elettroni e lacune in un semiconduttore, nel quale essi si ricombinano
40
emettendo luce. L’ emissione avviene pertanto all’ interno del materiale, ma solo
la luce che fuoriesce da questo costituisce radiazione effettivamente utilizzabile.
Una rappresentazione schematica della struttura di un LED è mostrata nella figura
35:
Fig. 35
Solo l’ emissione che avviene per angoli compresi tra - c e + c (dove
c è l' angolo critico per la riflessione totale) risulta in emissione dal dispositivo,
mentre la restante parte rimane intrappolata nel materiale sotto forma di modi
guidati. Un’ espressione approssimata per la frazione di luce effettivamente
emessa è data da
1
, dove n è l’ indice di rifrazione del materiale in cui avviene
2n 2
l’ emissione. Per un semiconduttore, come ad esempio GaAs, n = 3.5, e dunque
solo il 5% dell’ emissione è utilizzabile.
Un modo per risolvere il problema è quello di includere lo strato emissivo in
una cavità ottica: la struttura mostrata nella figura 35 infatti costituisce già di per
sé una cavità, delimitata però da “specchi” molto deboli (le superfici del
dielettrico), con la conseguenza che lo spettro di modi all’ interno è continuo;
ponendo invece il materiale in una microcavità costituita da specchi metallici ad
elevata riflettività si ottiene uno spettro di modi discreto, e si può dunque fare in
modo di lavorare in propagazione unimodale. Se nella cavità è presente solo il
modo fondamentale è più semplice ottimizzare l’ emissione, e si riducono i
possibili meccanismi di perdita. Con questo approccio si hanno dunque
principalmente due alternative:
41
-
bloccare l’ emissione che avviene attraverso modi che non contribuiscono
alla radiazione utile (modi guidati); ciò può essere fatto introducendo
microstrutture periodiche nel piano della cavità che impediscano la
propagazione di modi guidati introducendo una band-gap.
-
Invece di bloccare i modi guidati, si può provare a recuperarli cercando di
fare in modo che essi si trasformino in radiazione, e ciò avviene sempre
grazie a opportune strutture periodiche.
Il secondo metodo è in realtà più efficiente e si basa sull’ uso di un modo
guidato che faccia da gradino intermedio tra il processo di emissione nel materiale
e la radiazione. Tale modo è appunto il plasmone superficiale.
Consideriamo quindi una microcavità, la cui rappresentazione schematica è
riportata nella figura 36.
Fig. 36
Lo strato di dielettrico in cui avviene l’ emissione è incastrato tra due
specchi. All’ interno di esso è presente l’ emettitore vero e proprio, che possiamo
considerare come un dipolo oscillante forzato (dal momento che il campo
prodotto dal dipolo viene riflesso dalla struttura circostante e si riaccoppia con il
dipolo) immerso nella cavità.
Lo spettro della potenza dissipata è mostrato in figura 37:
42
Fig. 37
La potenza dissipata nell’ intervallo 0 < u < 0.5 è quella che può essere
irradiata (e della quale solo una parte alla fine sarà utilizzabile); per
0.5 < u < 0.75 si ha potenza intrappolata tra gli specchi superiori, mentre il picco
per u = 1.02 corrisponde all’ eccitazione del plasmone superficiale all’ interfaccia
tra lo specchio inferiore e il dielettrico. Ciò che si vuole fare è dunque:
-
massimizzare l’ accoppiamento tra la sorgente e il plasmone superficiale, e
cioè aumentare il più possibile la potenza trasferita dall’ emettitore a
quest’ ultimo.
-
massimizzare l’ accoppiamento tra il plasmone e la radiazione luminosa.
Per quanto riguarda il primo punto, consideriamo per semplicità il caso di una
sorgente immersa in un semispazio dielettrico limitato superiormente da un
semispazio metallico; il trasferimento di energia dall’ emettitore al plasmone può
essere ottimizzato variando la distanza del primo dal metallo, come è evidente dai
grafici seguenti (figura 38), in cui è mostrata la potenza trasferita dalla sorgente al
plasmone, alle onde superficiali dissipative e alla radiazione, in funzione della
suddetta distanza e per varie orientazioni del dipolo.
43
Fig. 38
Osservando poi la curva di dispersione del plasmone (k x ) , si può notare
che al crescere di kx aumenta la densità dei modi plasmonici attorno a un valore
asintotico di . A questa frequenza è dunque possibile l’ accoppiamento dell’
emettitore con un gran numero di modi.
44
Fig. 39 Curva di dispersione del plasmone all’ interfaccia metallo-dielettrico
Il problema di questa frequenza asintotica è che essa non è accordabile con
la frequenza della sorgente; vi sono tuttavia strutture più efficaci della singola
interfaccia metallo-dielettrico per supportare plasmoni superficiali, che offrono
inoltre anche una certa accordabilità, quali ad esempio strutture planari
multistrato.
Queste ultime si basano sull’ utilizzo di plasmoni superficiali accoppiati e tra
di esse si possono distinguere principalmente in due tipi di dispositivi:
-
strato metallico circondato da dielettrico;
-
cavità dielettrica delimitata da due sottili film metallici.
In entrambi i casi si hanno due possibili configurazioni di campo per i
plasmoni accoppiati (figura 40), associati a una distribuzione di carica simmetrica
o antisimmetrica sulle due interfacce.
Nel caso di strato metallico circondato da dielettrico, la configurazione
simmetrica (caso (a) nella figura 40) ha uno zero di campo nel metallo, quella
asimmetrica (caso (b)) ha invece più perdite in quanto presenta una maggiore
concentrazione di campo in esso.
La soluzione più efficace tuttavia è la cavità dielettrica delimitata da film
metallici, in quanto si può dimostrare che in questo caso, e in particolare per la
configurazione asimmetrica (caso (d)), si riesce ad accoppiare fino al 90% della
potenza emessa dalla sorgente con i plasmoni.
45
Fig. 40
Una volta trasferita la potenza i plasmoni accoppiati è ovviamente
necessario trasformare questi ultimi in radiazione luminosa. Anche in questo caso
vi sono varie possibilità, di cui si è già discusso, come l’ accoppiamento ATR o l’
introduzione di strutture periodiche. Le seconde sono particolarmente intressanti
in quanto consentono di ottenere l’ accordabilità in frequenza di cui si è parlato
poco fa, sfruttando la struttura a bande della curva di dispersione. Le bande sono
infatti in genere piatte ai bordi, dove si ha quindi un’ elevata densità di modi, e la
loro posizione spettrale può essere controllata variando il periodo del reticolo.
46
CONCLUSIONI
L’ esistenza dei plasmoni superficiali non è una scoperta degli ultimi anni; essi
furono studiati per la prima volta nel 1902 da Wood, che osservò delle anomalie
nello spettro di riflessione di un reticolo illuminato con luce in polarizzazione p.
Nel 1907, Rayleigh fu il primo a tentare una trattazione teorica del fenomeno con
un approccio basato sullo scattering, secondo il quale, in corrispondenza di certe
lunghezze d’ onda, la formazione di un nuovo ordine diffratto provocava una
ridistribuzione di energia negli altri ordini e le conseguenti anomalie nello spettro
di riflessione. Il concetto di eccitazione collettiva superficiale risale però solo agli
anni 50, quando venne introdotto per la prima volta da Pines e Bohm, e poi da
Ritchie. Ma è negli ultimi anni che la ricerca sui plasmoni superficiali ha avuto
maggior impulso, specialmente grazie alle potenziali opportunità che essi
sembrano offrire nel campo della progettazione di circuiti fotonici e delle
nanotecnologie. Tuttavia le applicazioni comprendono aree molto più vaste, dallo
sviluppo di sorgenti luminose, come LED e OLED (organic light-emitting diode),
e di lenti super-risolutive, alla progettazione di componenti non lineari. Nel
prossimo futuro, gli sforzi maggiori sono rivolti al raggiungimento dei seguenti
obiettivi:
-
progettare circuiti con interconnessioni metalliche di dimensioni minori
della lunghezza d’onda e dalle perdite confrontabili con quelle delle
tradizionali guide ottiche;
-
permettere il controllo attivo di segnali plasmonici mediante la
modulazione elettro-ottica, ottica e piezoelettrica, e tramite meccanismi di
guadagno, nelle strutture plasmoniche;
-
progettare componenti ottici plasmonici 2D in grado di accoppiare fibre a
singolo modo con circuiti plasmonici;
-
sviluppare nanolitografia plasmonica a dimensioni molto inferiori alla
lunghezza d’onda su larghe superfici.
47
BIBLIOGRAFIA
[1] H. Raether, “Surface plasmons on smooth and rough surfaces and on
gratings”, (Springer-Verlag, Berlin, 1998)
[2] A. V. Zayats, I. I. Smolyaninov, A. A. Maradudin, “Nano-optics of suface
plasmon polaritons”, Physics Reports vol.408, 2005, pp 131-314
[3] H. J. Simon, D.E. Mitchell, J. G. Watson, “Surface plasmons in silver films –
A novel undergraduate experiment”, American Journal of Physics vol.43, No.7,
July 1975, pp 630-636
[4] W. L. Barnes, A. Dereux, T. W. Ebbesen, “Surface plasmon subwavelength
optics”, Nature vol.424, 14 August 2003, pp 824-830
[5] M. Mansuripur, Lifeng Li, “What in the world are surface plasmons?”, Optics
& Photonics News, May 1997
[6] F. J. Garcìa-Vidal et al., “Localized surface plasmons in lamellar metallic
gratings”, Journal of Lightwave technology vol.17, No.11, IEEE November 1999,
pp 2191-2195
[7] M.B. Sobnack, W.C. Tan, N.P. Wanstall, T.W. Preist and J.R. Sambles,
“Stationary surface plasmons on a zero-order metal grating”, Physical Review
Letters vol.80, No.25, 22 June 1998, pp 5667-5670
[8] F. Przybilla, A. Degiron, J.Y. Laluet, C. Genet and T.W. Ebbesen, “Optical
transmission in perforated noble and transition metal films”, Journal of Optics
A:Pure and Applied Optics vol.8, 2006, pp 458-463
[9] J.A. Porto, F.J. Garcìa-Vidal, J.B. Pendry, “Transmission resonances on
metallic gratings with very narrow slits”, Physical Review Letters vol.83, No.14,
4 October 1999, pp 2845-2848
[10] E. Ozbay, “Plasmonics: merging photonics and electronics at nanoscale
dimensions”, Science vol.311, 13 January 2006, pp 189-193
[11] W.L. Barnes, “Electromagnetic crystals for surface plasmon polaritons and
the extraction of light from emissive devices”, Journal of Lightwave Technology
vol.17, No.11, IEEE November 1999, pp 2170-2182
48











