Università di Bologna - Corsi di Laurea Triennale in Ingegneria, II Facoltà - Cesena
Sessione invernale 2006 - Secondo appello - Prova scritta del corso di Fisica Generale L-B
(11 gennaio 2007)
Prof. Maurizio Piccinini
p
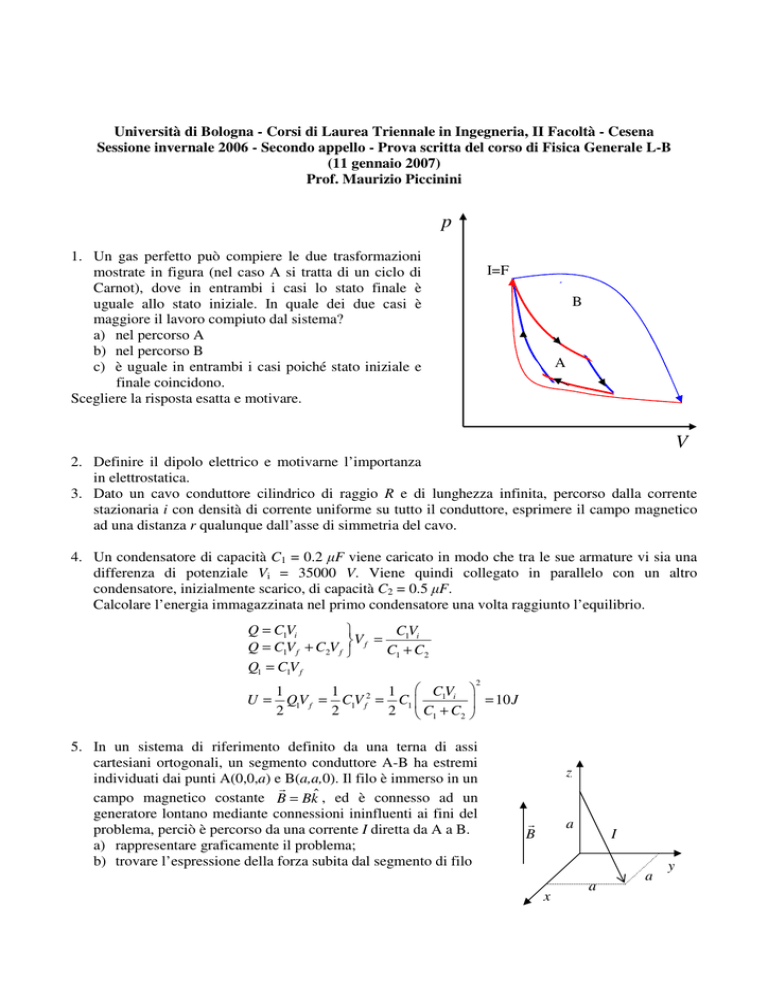
1. Un gas perfetto può compiere le due trasformazioni
mostrate in figura (nel caso A si tratta di un ciclo di
Carnot), dove in entrambi i casi lo stato finale è
uguale allo stato iniziale. In quale dei due casi è
maggiore il lavoro compiuto dal sistema?
a) nel percorso A
b) nel percorso B
c) è uguale in entrambi i casi poiché stato iniziale e
finale coincidono.
Scegliere la risposta esatta e motivare.
I=F
B
A
V
2. Definire il dipolo elettrico e motivarne l’importanza
in elettrostatica.
3. Dato un cavo conduttore cilindrico di raggio R e di lunghezza infinita, percorso dalla corrente
stazionaria i con densità di corrente uniforme su tutto il conduttore, esprimere il campo magnetico
ad una distanza r qualunque dall’asse di simmetria del cavo.
4. Un condensatore di capacità C1 = 0.2 µF viene caricato in modo che tra le sue armature vi sia una
differenza di potenziale Vi = 35000 V. Viene quindi collegato in parallelo con un altro
condensatore, inizialmente scarico, di capacità C2 = 0.5 µF.
Calcolare l’energia immagazzinata nel primo condensatore una volta raggiunto l’equilibrio.
Q = C1Vi
C1Vi
Vf =
Q = C1V f + C2V f
C1 + C2
Q1 = C1V f
2
1
1
1 CV
U = QV
C1V f2 = C1 1 i = 10 J
1 f =
2
2
2 C1 + C2
5. In un sistema di riferimento definito da una terna di assi
cartesiani ortogonali, un segmento conduttore A-B ha estremi
individuati dai punti A(0,0,a) e B(a,a,0). Il filo è immerso in un
campo magnetico costante B = Bkˆ , ed è connesso ad un
generatore lontano mediante connessioni ininfluenti ai fini del
problema, perciò è percorso da una corrente I diretta da A a B.
a) rappresentare graficamente il problema;
b) trovare l’espressione della forza subita dal segmento di filo
z
a
B
x
I
a
a
y
dF = Idl ∧ B ⇒ F = I ( B − A) ∧ B = I (aiˆ + ajˆ − akˆ) ∧ B
iˆ ˆj kˆ
F = I a a − a = IBa(iˆ − ˆj )
0 0
B
6. Un gas perfetto si trova inizialmente in uno stato
definito dai valori pA, VA e TA delle variabili
termodinamiche pressione, volume e temperatura. Il gas
subisce prima una espansione isobara fino ad uno stato
B caratterizzato dal volume VB = 2 VA, quindi una
trasformazione isoterma che lo porta allo stato C con
pressione pC = pA/2 e finalmente una trasformazione
isocora che lo porta ad uno stato D con pressione pD =
pA.
a) Rappresentare le trasformazioni in un diagramma p
– V.
b) Esprimere i valori di p, V e T negli stati B,C e D in
funzione di pA, VA e TA.
A
p pA
V VA
T TA
B
pA
2VA
2TA
C
pA/2
4VA
2TA
pV = nRT
VB / TB = VA / TA
pV = nRT
pD / TD = pC / TC
p
⇒ TD = ( pD / pC ) TC = 2TC = 4TA
B
pA/2
pV = nRT
pCVC = pBVB
D
C
VA
D
pA
4VA
4TA
⇒ TB = (VB / VA ) TA = 2TA
A
pA
2VA
⇒ VC = ( pB / pC ) VB = 2VB = 4VA
V












