Onde piane a più dimensioni
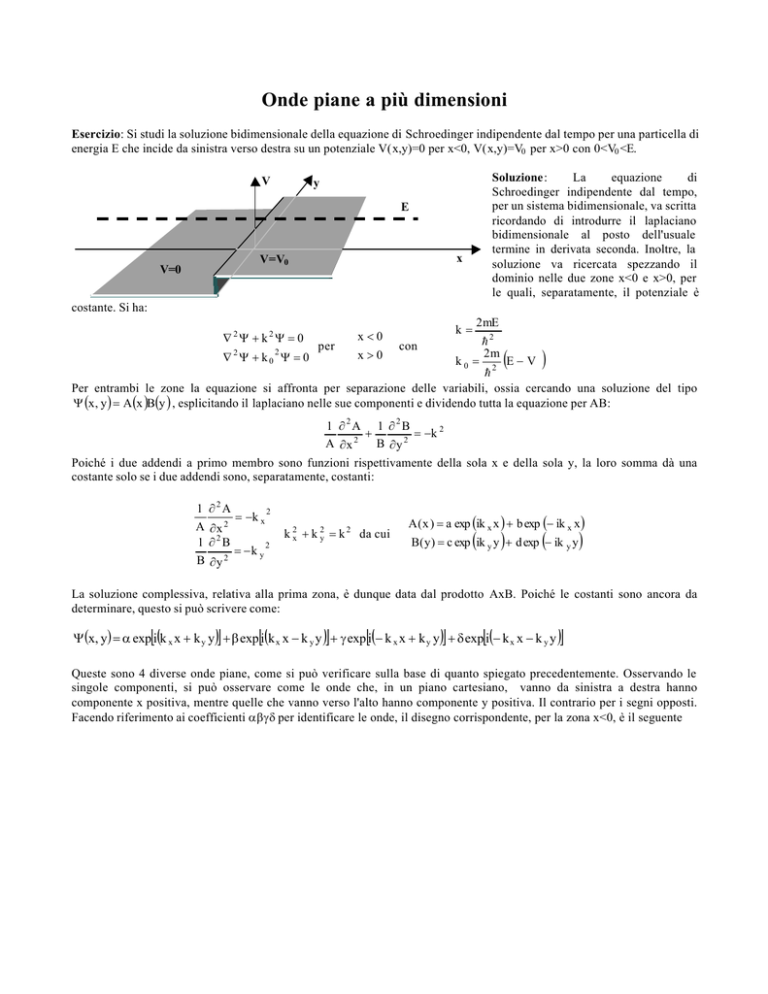
Esercizio: Si studi la soluzione bidimensionale della equazione di Schroedinger indipendente dal tempo per una particella di
energia E che incide da sinistra verso destra su un potenziale V(x,y)=0 per x<0, V(x,y)=V0 per x>0 con 0<V0 <E.
V
Soluzione:
La
equazione
di
Schroedinger indipendente dal tempo,
per un sistema bidimensionale, va scritta
ricordando di introdurre il laplaciano
bidimensionale al posto dell'usuale
termine in derivata seconda. Inoltre, la
soluzione va ricercata spezzando il
dominio nelle due zone x<0 e x>0, per
le quali, separatamente, il potenziale è
y
E
x
V=V0
V=0
costante. Si ha:
∇2Ψ + k2Ψ = 0
2
∇ Ψ + k0 Ψ = 0
2
per
x<0
x>0
k=
2 mE
con
k0 =
h2
2m
(
)
E−V
h2
Per entrambi le zone la equazione si affronta per separazione delle variabili, ossia cercando una soluzione del tipo
Ψ (x , y ) = A (x )B(y ) , esplicitando il laplaciano nelle sue componenti e dividendo tutta la equazione per AB:
1 ∂2A 1 ∂2B
+
= −k 2
A ∂x 2
B ∂y 2
Poiché i due addendi a primo membro sono funzioni rispettivamente della sola x e della sola y, la loro somma dà una
costante solo se i due addendi sono, separatamente, costanti:
1
A
1
B
∂2A
= −k x
2
2
= −k y
2
2
∂x
∂2B
∂y
k 2x + k 2y = k 2 da cui
A ( x ) = a exp (ik x x ) + b exp (− ik x x )
(
)
(
B( y ) = c exp ik y y + d exp − ik y y
)
La soluzione complessiva, relativa alla prima zona, è dunque data dal prodotto AxB. Poiché le costanti sono ancora da
determinare, questo si può scrivere come:
[
]
[
]
[
]
[
]
Ψ (x, y) = α exp i(k x x + k y y) + β exp i(k x x − k y y ) + γ exp i(− k x x + k y y) + δ exp i(− k x x − k y y )
Queste sono 4 diverse onde piane, come si può verificare sulla base di quanto spiegato precedentemente. Osservando le
singole componenti, si può osservare come le onde che, in un piano cartesiano, vanno da sinistra a destra hanno
componente x positiva, mentre quelle che vanno verso l'alto hanno componente y positiva. Il contrario per i segni opposti.
Facendo riferimento ai coefficienti αβγδ per identificare le onde, il disegno corrispondente, per la zona x<0, è il seguente
y
β
γ
x
α
δ
Si noterà il parallelismo α−δ e β−γ, corrispondente ad una completa inversione dei segni delle componenti x e y nelle
esponenziali, mentre la inversione di uno solo di questi dà la specularità rispetto all'asse x.
Il medesimo risultato si otterrebbe, con un disegno speculare rispetto all'asse y, per la soluzione nel semipiano x>0,
naturalmente con k0 a sostituire k (e quindi k0x al posto di kx e k0y al posto di ky ), e diverse costanti α0 , β0 , γ0 , δ0 , ad indicare
la combinazione lineare di altrettante onde piane.
[
]
[
]
[
]
[
]
Ψ0 (x, y) = α 0 exp i(k 0 x x + k 0 y y ) + β0 exp i (k 0 x x − k 0 y y ) + γ 0 exp i(− k 0 x x + k 0 y y) + δ0 exp i(− k 0 x x − k 0 y y)
∂Ψ
∂x
Ψ (0 , y ) = Ψ0 (0 , y ) ,
Le due condizioni di raccordo
=
x= 0
∂Ψ0
∂x
in x>0
danno subito una indicazione: vi sono 6 costanti
x= 0
su 8 che non verranno determinate, e che quindi si possono scegliere a piacere.
Andiamo quindi secondo convenienza: ci aspettiamo che il sistema, nella sua forma più semplice, tratti il caso di un'onda
inclinata che incide da destra, che in parte viene riflessa ed in parte trasmessa. In questo sistema, tre onde in tutto saranno
presenti, e quella che prendiamo come onda incidente può essere presa di ampiezza unitaria.
Scegliendo come onda incidente quella identificata da α (e quindi α=1), si esclude subito l'altra incidente da sinistra, β, ed
entrambe le onde incidenti da destra a sinistra nella regione x>0 (δ0 e γ0 ) perché qui sopravviverà solo un'onda trasmessa,
che quindi si propagherà verso le x crescenti (k0x positivo).
Le soluzioni, quindi, sono momentaneamente semplificate in
[
]
[
]
[
y)]
]
Ψ (x, y) = exp i(k x x + k y y ) + γ exp i(− k x x + k y y) + δ exp i(− k x x − k y y)
[
]
[
Ψ0 (x, y) = α 0 exp i(k 0 x x + k 0 y y) + β0 exp i(k 0 x x − k 0 y
x<0
x>0
Tuttavia, vi sono ancora 4 costanti, mentre possiamo determinarne solo due dalle condizioni al contorno.
Un modo abbreviato per vedere cosa eliminare è quello che prevede, in analogia con quanto è noto nei fenomeni ondulatori
classici, che se l'onda incidente viaggia dal basso all'alto, anche l'onda riflessa e quella trasmessa faranno altrettanto. In
conseguenza di questo, le onde con ky negativo possono essere eliminate. In conclusione:
[
]
[
]
Ψ (x, y) = exp i(k x x + k y y) + Re xp i(− k x x + k y y)
[
]
Ψ0 ( x, y ) = T exp i(k 0 x x + k 0 y y)
x<0
x>0
Le due costanti ancora indeterminate sono state ribattezzate T e R ad indicare l'onda trasmessa e quella riflessa
rispettivamente.
La prima condizione di raccordo, ora, dà subito: (1 + R ) exp(ik y y) = T exp(ik 0 y y) che può essere soddisfatta per qualsiasi
valore di y solo se k0y =ky , così da poter semplificare le esponenziali ed avere solo la relazione tra le costanti T=1+R.
Aggiungendo la condizione sulla derivata rispetto a x calcolata in x=0, si ottiene: k x(1-R)=k0xT da cui
R=
T=
k x − k 0x
k x + k 0x
2k x
k x + k 0x
La soluzione finale, che include le espressione di R e T e la uguaglianza di ky tra le due regioni è quindi:
[(
)]
Ψ (x , y ) = exp i k x x + k y y +
Ψ 0 (x , y ) =
[(
2k x
k x − k 0x
k x + k 0x
[(
exp i − k x x + k y y
)]
)]
exp i k 0 x x + k y y
k x + k 0x
La relazione ha molte analogie (come è ovvio) con quella del caso undimensionale, al quale peraltro si riconduce se si
considerano onde incidenti perpendicolarmente allo scalino di potenziale (ky =0, per cui k=kx, k0 =k0x).
Tuttavia, nella forma bidimensionale, la relazione tra i coefficienti R e T e le energie E e V0 è più complessa. Infatti le
componenti x del vettore d'onda dipendono da E, V0 e k y.
kx =
2 mE
h
2
− ky
2
, k 0x =
2m
h
2
(E − V0 ) − k y 2
Al discostarsi della inclinazione dell'onda incidente dalla direzione perpendicolare allo scalino sopra considerata, ky
aumenta e corrispondentemente kx diminuisce. Al limite, per onde radenti, si ha ky =k e kx =0.
Tuttavia, prima di raggiungere questo estremo, nella regione in cui si propaga l'onda trasmessa la radice si annulla, e k0x va
a zero. In questo caso il coefficiente di riflessione diventa unitario, ossia si ha riflessione totale. Oltre questa inclinazione di
incidenza, in x>0 si propagano solo onde evanescenti, che scompaiono esponenzialmente a breve distanza dall'interfaccia.
2m
E' facile calcolare l'angolo critico: quando k0x si annulla, si ha k y =
h
2
(E − V0 ) , e quindi
kx =
2m
h2
V0 , per cui la
tangente dell'angolo θc di incidenza è data da ky /kx ,
E − V0
ϑ c = a tan
V0
Infine, riconoscendo nel termine ky /k il seno dell'angolo di propagazione delle onde rispetto all'asse x, si ha la versione
E − V0
sen ϑ
meccanica della legge di Snell:
=
.
E
sen ϑ 0
La figura a fianco mostra le relazioni tra
onda incidente, onda riflessa e onda
trasmessa, tramite le componenti dei vettori
d'onda.
ky
-ky
La costruzione coincide a quella usata per la
θ0
k0x
legge di Snell per la rifrazione. Si noti come
-kx
nell'ultima formula il rapporto tra gli indici
x
di rifrazione sia rappresentato dal rapporto
θ
tra i valori di E-V(x) (sotto radice quadrata).
Questo apre la porta alla costruzione di
sistemi "ottici" (lenti, prismi, microscopi)
ky
basati su onde di Schroedinger.
Sapendo che il più piccolo oggetto
kx
osservabile in un microscopio (limite di
risoluzione) è dell'ordine di una lunghezza d'onda (il che limita la microscopia ottica alla osservazioni di dettagli non più
piccoli di 1 µm), si provi a calcolare il limite di risoluzione teorico di un microscopio elettronico che usi elettroni di energia
pari a 100 keV.
R
y
T










