SECONDA LEZIONE:
interazione della radiazione con la materia
misure sperimentali e loro statistica
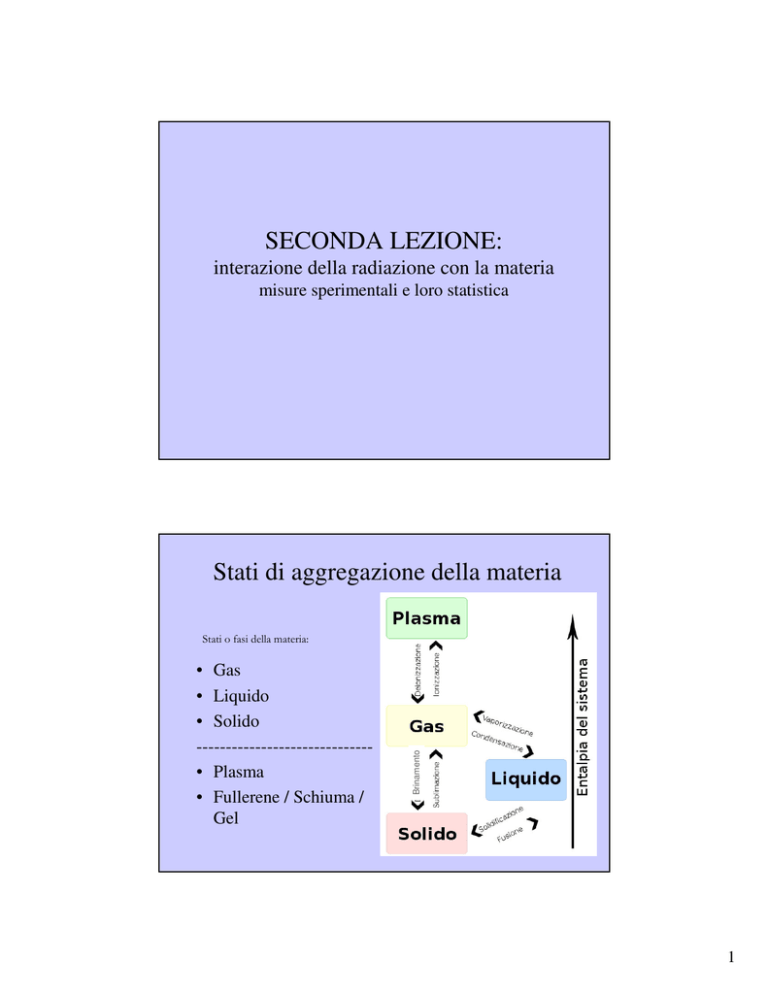
Stati di aggregazione della materia
• Gas
• Liquido
• Solido
-----------------------------• Plasma
• Fullerene / Schiuma /
Gel
Brinamento
Stati o fasi della materia:
1
RADIAZIONI E MATERIA
lunghezza d’onda
λ (m)
10-11
10-10
10-9
1Å
10-8
10-7
10-6
10-5
10-4
1 µm
1 nm
10-3
10-2
10-1
1
102
10
103
1 mm
energia
1 MeV
1 keV
1 eV
Regioni spettrali
RAGGI X
transizioni
elettroni
interni
Processi fisici coinvolti
ULTRAVIOLETTO
transizioni
elettroni
esterni
VISIBILE
RAGGI γ
eccitazione
nucleare e
atomica
INFRAROSSO
vibrazioni
molecolari
(bending, stretching)
ONDE RADIO
MICROONDE
rotazioni
molecolari
risonanza
spinelettrone
risonanza
magnetica
nucleare
ROSSI
GIALLI
VERDI
BLU
VIOLA
590-780
560-590
490-560
450-490
380-450
regioni spettrali dei principali colori (in nanomentri)
INFRAROSSO
ULTRAVIOLETTO
N.B.: colori spettrali cioè cui corrisponde una singola lunghezza d’onda
2
PROCESSI DI INTERAZIONE TRA RADIAZIONE E MATERIA
radiazione
incidente
radiazione
riflessa
diffusa
radiazione
riflessa
speculare
radiazione assorbita
radiazione
trasmessa
rifrazione,
diffusione e
assorbimento
trasmissione
incidenza e
riflessione
INTERAZIONE RADIAZIONE-MATERIA
Oggetto o campione
x (spessore)
I0
energia
entrante
fenomeni
di interazione
energia
assorbita
I
energia
uscente
Legge di assorbimento
I = I 0 e −α x
α = coefficiente di assorbimento
1
x
I0
I
α = ln
3
• Rappresentazione grafica delle misure: lo SPETTRO:
Ag (scattering)
2000
1800
1600
CPS
1400
PICCHI: l’altezza è proporzionale al segnale
1200
1000
800
600
400
Sr
Pb
Zn
Fe
200
Zr
0
0
1
2
3
4
5
6
7
8
9
10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27
Energy (KeV)
• indicazione di ascissa, ordinata e u.d.m., risoluzione, ...
L’analisi dimensionale
Uso delle unità di misura
GRANDEZZE FISICHE
Tempo
spazio
massa (peso)
Unità di misura
fondamentali:
Secondi
Metro
Kilogrammo
Unità di misura derivate p.es. energia [Joule]=[kg m2 s2] o la frequenza
Hz = [s-1]
Unità convenzionali NON fondamentali e non direttamente derivate
p.es. keV per l’energia
4
La misura
incertezza sulla misura
- errori sistematici (eliminabili, ad es. di taratura dello strumento, ...)
- errori casuali (NON eliminabili)
I numeri: cifre decimali e cifre significative (sensibilità dello strumento)
L=5,45m +0,54
4,91<L< 5,99
sensibilità=0,01m
ha tre cifre significative
Caratteristiche della strumentazione:
- SENSIBILITÀ: minima grandezza rilevabile
- RISOLUZIONE: capacità di distinguere
- INTERVALLO operativo (=range)
- PORTATA: massima quantità rilevabile (problemi di saturazione, ...)
- LIMITI di applicazione (profondità di penetrazione, applicabilità in aria
ecc)
Misura qualitativa e quantitativa:
• Qualitativo: identificazione degli elementi caratteristici presenti
• Quantitativo: misura della coincentrazione relativa dei vari composti trovati.
Dati ed errori
g = 9,82 + 0,02385 m/s2
Gli errori sperimentali dovrebbero essere arrotondati
a una cifra significativa
L’ultima cifra significativa deve essere dello stesso
ordine di grandezza (cioè nella stessa posizione
decimale) dell’errore
Non 6051,78 + 30
ma
6050 + 30
5
Cifre significative
stipendio = 1330,27 €
7 centesimi è una cifra significativa ?
In generale la cifra significativa è l’ultima letta dallo strumento, ovvero
quella su cui vi è indeterminazione
L’altezza di un uomo è 177 cm
c.s. è il secondo 7
Il numero di battute su un foglio A4 è 2000
c.s. è il terzo 0
Attenzione non è la risoluzione dello strumento anche se ne è determinata
Principio generale maggiore è il numero di cifre significative in un dato
meno chi fornisce la misura è credibile.
LA MISURA E LA SUA INCERTEZZA
• Un risultato senza errore non significa molto e può
essere fuorviante
– Ad es. il mese scorso 25 omicidi a Milano e questo mese
solo 20, grande successo!!
– Come valutare bontà risultato?
• “Prof. La mia misura è 93035 invece che 96485, aiuto, cosa
faccio?” ma l’errore tipico è 4000 circa…
A che precisione mirare? Come valutare precisione di
una strumentazione, errore di un risultato?
•
•
•
•
– L’incompreso mondo della probabilità:
% di cosa?
Attenzione alla probabilità condizionata!
Il rischio medico e i falsi positivi
“la fallacia dell’accusatore”
6
Notazione esponenziale
1 m = 103 mm = 106 µm ...
1 µm = 10-3 mm = ?? m
Ordini di grandezza
Grafici con assi logaritmici: riportano
sull’asse il valore dell’esponente in base 10
Misure accurate
Misure ripetibili hanno
una bassa incertezza cioè
i dati si discostano poco
da un valor medio
Misure ripetibili
Misure accurate
PRECISIONE
Misure ripetibili
Misure accurate
hanno un buon grado
di approssimazione al
valor vero
Valor medio
Valor vero
7
statistica
N dati: x1, x2, x3……xn
Media:
x=
x1 + x2 + ... x n
N
Media pesata:
x=
x1 ⋅ f1 + x 2 ⋅ f 2 + ... x n ⋅ f n
f1 + f 2 + ... f n
Deviazione standard: quanto mediamente un dato differisce dal valor medio, è un
buon indice dell’errore di una misura realizzata attraverso più misure sperimentali.
x ±σ x
Valore di una misura sperimentale dedotta da N misure :
Come si distribuiscono dei dati con
un errore casuale?
distribuzione gaussiana
Frequenza del dato
12
10
8
6
4
2
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Valore del dato
8
Statistica
Distribuzione “Gaussiana”
Valor medio Deviazione standard
Il risultato di una misura fornisce i seguenti valori
xM= 3,5 σ=5,0
È affidabile?
--------------------------------------------------------------Il valor medio di due misure 2,0 e 5,1 è
xM = 3,55
Ma la a misura media vale 3,5 !
9












