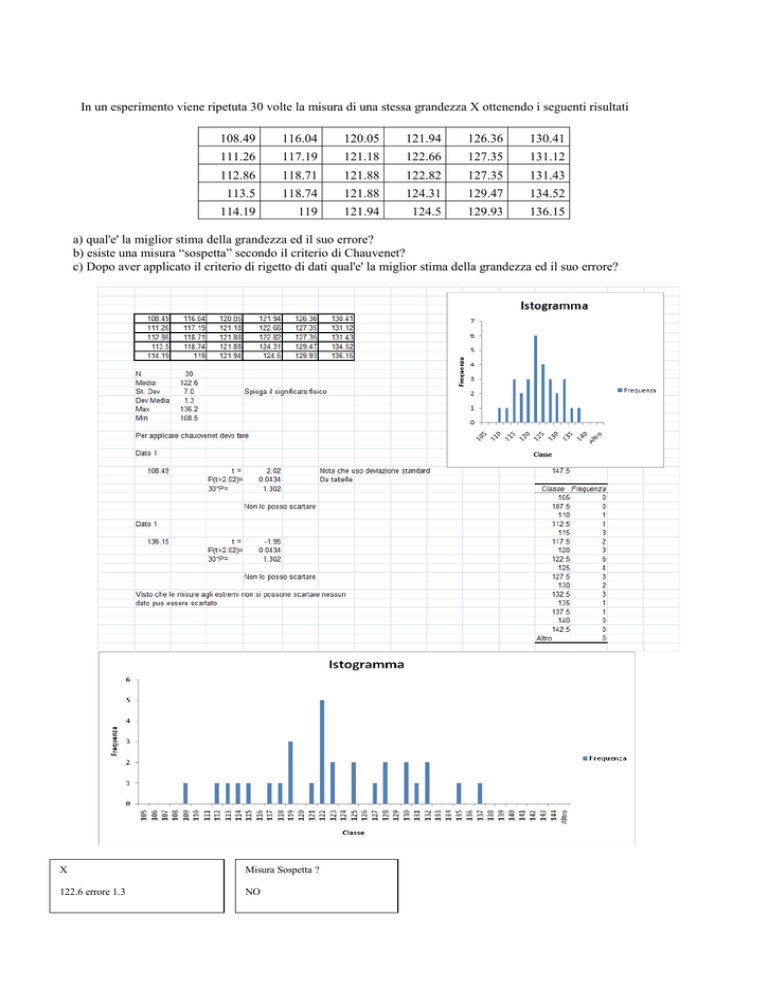
In un esperimento viene ripetuta 30 volte la misura di una stessa grandezza X ottenendo i seguenti risultati
108.49
116.04
120.05
121.94
126.36
130.41
111.26
117.19
121.18
122.66
127.35
131.12
112.86
118.71
121.88
122.82
127.35
131.43
113.5
118.74
121.88
124.31
129.47
134.52
114.19
119
121.94
124.5
129.93
136.15
a) qual'e' la miglior stima della grandezza ed il suo errore?
b) esiste una misura “sospetta” secondo il criterio di Chauvenet?
c) Dopo aver applicato il criterio di rigetto di dati qual'e' la miglior stima della grandezza ed il suo errore?
X
Misura Sospetta ?
122.6 errore 1.3
NO
Poiché l‟intercetta è differente da zero allora esiste evidenza di errore sistematico
La densità di un liquido viene misurata da 3 studenti differenti con metodologie e strumentazione
differente. I valori medi e gli errori delle medie sono riportati in tabella :
Studente A
Studente B
Studente C
348.8 ± 2.5 Kg/m3
352.0 ± 4.0 Kg/m3
353.2 ± 2.0 Kg/m3
Per 10 misure
Per 10 misure
Per 10 misure
a) si dica se i 3 valori della densità sono compatibili a livello di confidenza del 5%
b) si calcoli il miglior valore della densità ed il suo errore tenendo conto del risultato del punto
precedente.
c) Se lo studente B ripetesse la misura 20 volte (nelle stesse condizioni sperimentali) di quanto
si ridurrebbe la sua incertezza?
Sono consistenti ?
densità
sigma
Una distanza K dipende dalle osservabili „a‟, „‟ secondo la legge K = a tan(). Si supponga che si
voglia ottenere una stima sperimentale dell‟osservabile K e del suo errore attraverso la misura di
„a‟, e „‟. Si supponga anche che nella misura in questione a 0.732 m (a 1 mm) e /3
radianti ( 0.0001 radianti). Stimare l‟errore percentuale su K che si otterrebbe con una misura e
identificare se nella misura pesa di più un errore nella misura della lunghezza o nella misura
dell‟angolo
Un campione radioattivo contiene n=3.4 1017 nuclei ciascuno dei quali ha, ogni secondo, la
probabilità p=0.4 10-16 di decadere. Calcolare:
1) il numero medio di decadimenti al secondo ed al minuto
2) La deviazione standard attese nelle due distribuzioni
3) la probabilità di non osservare in un secondo alcun decadimento
4) la probabilità di osservare 834 decadimenti in un minuto
Poiche la distribuzione ha un valore medio molto superiore ad uno, uso una gaussiana. Attenzione che la
Poissoniana è definita per numeri interi mentre la gaussiana è definita nel campo reale