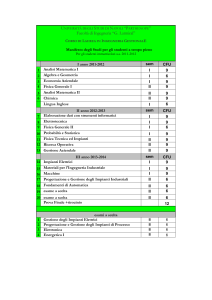
Ingegneria dei Sistemi Elettrici_2b
(ultima modifica 08/03/2010)
M. Usai
Ingegneria dei Sistemi Elettrici_2b
27
L’integrale ∫ A ⋅ d s
S
è un integrale superficiale ed è un integrale doppio in due
dimensioni. Esso è il flusso del vettore A attraverso la
superficie di area S.
Il versore d s normale alla superficie S
• è uscente dalla superficie se la superficie è chiusa e
• dipende dalla direzione nella quale è percorso il contorno
della superficie se la superficie è aperta e si determina con al
regola della mano destra.
an
an
an
M. Usai
Ingegneria dei Sistemi Elettrici_2b
28
Le grandezze elettromagnetiche generalmente sono grandezze
scalari e vettoriali che dipendono dal tempo e dal punto o posizione
( coordinate spaziali), ossia complessivamente dipendono da
quattro variabili:
•il tempo e
•le tre coordinate spaziali.
Sono quindi importanti i metodi per definire la velocità spaziale
di variazione di un campo scalare per un tempo stabilito.
Si devono sviluppare le derivate parziali rispetto alle tre coordinate
e poiché la velocità di variazione può essere diversa nelle diverse
direzioni, sarà necessario introdurre un vettore che definisca la
velocità spaziale di cambiamento del campo scalare in un
determinato punto e un determinato tempo.
M. Usai
Ingegneria dei Sistemi Elettrici_2b
29
V(u1,u2,u3)
Gradiente di un campo scalare
V è una grandezza scalare funzione di tre
coordinate ui ( potenziale elettrico, temperatura ,
pressione, tasso di umidità).
P2
α
dl
P1 d n
P3
an
V+dV
V
dV
Per la stessa variazione dV, la velocità di variazione è dl diversa
lungo d n , perché dn è il percorso più piccolo per passare dalla
superficie a potenziale V a quella a potenziale V+dV.
M. Usai
Ingegneria dei Sistemi Elettrici_2b
30
Sulla base di queste considerazioni sorge l’esigenza di definire
un vettore che rappresenti sia l’ampiezza che la direzione della
massima velocità spaziale di incremento di una grandezza
scalare come; gradiente della grandezza scalare,
ossia il vettore che rappresenta il rapporto massimo fra la
variazione di V e la lunghezza dl
dV
grad V = ∇ V = a n
dn
dV dV dn
dV
dV
=
=
cosα =
an ⋅ al
dl
dn dl
dn
dn
∂
∂
∂
⎧
⎪∇ = a x ∂x + a y ∂y + a z ∂z
⎪
in coordinate cartesiane
⎨
⎪∇ V = ⎛⎜ a x ∂ + a y ∂ + a z ∂ ⎞⎟V
⎪⎩
∂z ⎠
∂y
⎝ ∂x
M. Usai
Ingegneria dei Sistemi Elettrici_2b
31
Si definisce divergenza di un vettore di campo A in un punto il
flusso netto uscente dalla superficie A per unità di volume,
quando il volume tende a zero:
A⋅d s
∫
div A = ∇ ⋅ A = lim
S
∆v →0
In coordinate cartesiane:
M. Usai
∆v
∂Ax ∂Ay ∂Az
∇ ⋅ A = div A =
+
+
∂x
∂y
∂z
Ingegneria dei Sistemi Elettrici_2b
32
La divergenza in coordinate cilindriche:
1 ∂r ∂Ar 1 ∂Aφ ∂Az
∇ ⋅ A = div A =
+
+
r ∂r
r ∂φ
∂z
La divergenza in coordinate sferiche :
1 ∂ (R 2 AR )
1 ∂ ( Aθ sinθ )
1 ∂ Aφ
∇ ⋅ A = div A = 2
+
+
R
∂R
R sinθ
∂θ
R sinθ ∂φ
M. Usai
Ingegneria dei Sistemi Elettrici_2b
33
Teorema della divergenza
Il flusso totale di un vettore uscente da una superficie chiusa
qualunque A è uguale all’integrale della divergenza del vettore,
esteso al volume V racchiuso dalla superficie stessa:
∫ A ⋅ d s = ∫ div A dv
S
V
Se la divergenza è uguale a zero in tutti i punti del campo, il
campo è solenoidale.
Se il campo è solenoidale, il flusso attraverso una qualunque
superficie contenuta nel campo è uguale a zero.
M. Usai
Ingegneria dei Sistemi Elettrici_2b
34
Integrale lineare di un vettore
L’integrale lineare di un vettore A lungo un tratto di curva
delimitato da due punti M e N é:
N
N
∫ A ⋅ d l = ∫ A cosβ dl
M
M
Il valore dell’integrale dipende :
• dal tratto di curva percorso tra M e N
• dalle posizioni di punti M e N
M. Usai
A
P
β
t
N
M
Ingegneria dei Sistemi Elettrici_2b
35
Il campo è irrotazionale quando l’integrale lineare tra due punti
qualsiasi appartenenti al campo, non dipende dal tratto di curva
che unisce i due punti M e N, ma solo dalla posizione dei due
punti:
N
∫ A ⋅ dl = k per qualsialsi percorso M N
M
in particolare
N
M
M
N
∫ A ⋅ dl = − ∫ A ⋅ dl
inoltre
∫ A ⋅ dl = 0
dove l é un percorso chiuso
l
M. Usai
Ingegneria dei Sistemi Elettrici_2b
36
Se A è irrotazionale ammette un potenziale V, ossia:
dV = A ⋅ d l
N
VM − V N = ∫ − dV
M
A = − gradV
M. Usai
Ingegneria dei Sistemi Elettrici_2b
37
Il rotazionale o rotore di un vettore A nel punto P é:
rot A = ∇ × A
ossia, é un vettore la cui
•ampiezza è la massima circuitazione del vettore A per unità di
area, quando questa tende a zero e
•la cui direzione è normale alla direzione dell’area orientata che
rende massima la circuitazione.
In coordinate cartesiane:
⎛ ∂Az ∂A y ⎞
⎛ ∂Ay ∂Ax ⎞
⎛ ∂Ax ∂Az ⎞
⎟⎟ + a y ⎜
∇ × A = a x ⎜⎜
−
−
−
⎟
⎟ + az⎜
∂x ⎠
∂y ⎠
∂z ⎠
⎝ ∂z
⎝ ∂x
⎝ ∂y
ax
∂
∇× A =
∂x
Ax
M. Usai
ay
∂
∂y
Ay
az
∂
∂z
Az
Ingegneria dei Sistemi Elettrici_2b
38
Il rotore in coordinate cilindriche:
ar
1 ∂
∇× A =
r ∂r
Ar
aφ r
∂
∂φ
rAφ
az
∂
∂z
Az
Il rotore in coordinate sferiche:
aR
∂
1
∇× A = 2
R sinθ ∂R
AR
M. Usai
aθ R a φ R sinθ
∂
∂
∂θ
∂φ
RAθ RsinθAφ
Ingegneria dei Sistemi Elettrici_2b
39
Il rot A gode delle seguenti importanti proprietà:
I° Identità nulla: rot (grad (V)) = ∇ × (∇ V) ≡ 0
Il rotore del gradiente di un campo scalare è uguale a zero.
II° Identità nulla: div (rot (A)) = ∇ ⋅ (∇ × A) ≡ 0
La divergenza del rotore di un campo vettoriale é uguale a zero.
Teorema di Stokes:
∫ (∇ × A )⋅ ds = ∫ A ⋅ dl
S
C
L’integrale superficiale del rotore di un campo vettoriale su una
superficie aperta è uguale all’integrale lineare del vettore lungo
la linea chiusa che delimita il contorno della superficie.
M. Usai
Ingegneria dei Sistemi Elettrici_2b
40
Nello studio dei campi vettoriali è conveniente rappresentare le
variazioni di campo graficamente con linee di campo
direzionali o orientate chiamate linee di campo o linee di
flusso.
Esse danno una visione della distribuzione del campo, indicando
in ciascun punto:
• la direzione del campo vettoriale con il verso delle linee
• l’ampiezza attraverso la densità delle linee ( nei punti dove le
linee sono più fitte il campo è più intenso).
La superficie di un volume definito all’interno di un campo,
racchiude una sorgente (source), se le linee di flusso sono
uscenti.
M. Usai
Ingegneria dei Sistemi Elettrici_2b
41
Se la divergenza di una grandezza vettoriale che definisce
un campo è nulla, il campo è solenoidale,
Se il rotore di una grandezza vettoriale che definisce un
campo è nullo, il campo è irrotazionale.
I campi vettoriali possono essere classificati in base al fatto
che essi siano solenoidali, irrotazionali e non.
M. Usai
Ingegneria dei Sistemi Elettrici_2b
42
Un campo vettoriale generico ha sia la divergenza che il
rotore diversi da zero e può essere considerato come la somma
di un campo solenoidale e di un campo irrotazionale.
Teorema di Helmhotz
Un campo vettoriale (funzione vettoriale puntuale) è
determinato dalla somma della divergenza del potenziale
scalare e del rotore del potenziale vettoriale, quando la sua
divergenza e il suo rotore sono ovunque definiti:
F = −∇V + ∇ × A
M. Usai
Ingegneria dei Sistemi Elettrici_2b
43
I campi possono essere classificati in :
• Campi variabili rapidamente: nei quali i fenomeni di
propagazione spaziale non sono trascurabili;
• Campi Statici: nei quali le grandezze che caratterizzano il
campo sono costanti al variare del tempo. Essi sono tempoinvarianti e in essi sono nulle le correnti di spostamento e le
f.e.m indotte;
• Campi quasi statici: nei quali le grandezze variano lentamente,
ossia le derivate temporali delle grandezze di campo sono
trascurabili rispetto alla loro velocità di propagazione nello
spazio. Inoltre le grandezze che caratterizzano il campo variano
nello stesso modo in un qualunque punto dello spazio.
M. Usai
Ingegneria dei Sistemi Elettrici_2b
44
I campi quasi statici si classificano in:
• Campi tempovarianti con legge armonica stazionaria
(sinusoidale). Per essi è conveniente rappresentare le variabili in
forma vettoriale.
• Campi tempovarianti con legge non armonica stazionaria.
• Nel caso di campi quasi statici le leggi di Maxwell si riducono ad
equazioni di diffusione.
Saranno trattati campi statici e quasi statici.
M. Usai
Ingegneria dei Sistemi Elettrici_2b
45
Lo studio dei campi statici o quasi statici trova applicazione
in:
• macchine elettriche rotanti;
• trasformatori;
• attuatori (relé contattori);
• testine magnetiche;
• schermature;
• bobine per acceleratori e macchine da fusione;
• potenziali elettrostatici: isolatori, passanti, connettori.
M. Usai
Ingegneria dei Sistemi Elettrici_2b
46
Lo studio dei campi rapidamente variabili o dinamici trova
applicazione in:
• Guide d’onda,
• Antenne,
• Cavità risonanti,
• Filtri
M. Usai
Ingegneria dei Sistemi Elettrici_2b
47
Un generico problema di campo può essere risolto facendo
ricorso a metodi analitici oppure a metodi numerici.
I metodi analitici sono particolarmente indicati nel caso
bidimensionale ed in presenza di mezzi lineari omogenei ed
isotropi. Essi sono stati ampiamente sviluppati durante il
secolo scorso e consentono di ottenere delle soluzioni esatte.
I principali metodi analitici utilizzati per la risoluzione di
problemi di campo elettromagnetico sono:
• metodo delle immagini;
• soluzioni in forma chiusa delle equazioni di Maxwell
espresse in forma di serie convergenti;
• metodi di trasformazioni conformi.
M. Usai
Ingegneria dei Sistemi Elettrici_2b
48
I metodi numerici sono applicabili anche nel caso tridimensionale
e nel caso di mezzi non lineari, non omogenei ed anisotropi.
Essi consentono di ottenere delle soluzioni approssimate e si sono
sviluppati con l'avvento dei calcolatori elettronici, quindi da circa
trent'anni, ma solo negli ultimi dieci anni hanno trovato uno
sviluppo nell'ambito progettuale-industriale.
I principali metodi numerici utilizzati per la risoluzione di
problemi di campo elettromagnetico sono:
• metodo delle differenze finite
• metodo degli elementi finiti
• metodo BEM ( Boundary Elements Method ).
M. Usai
Ingegneria dei Sistemi Elettrici_2b
49
Il problema della risoluzione di equazioni integrodifferenziali di campo è comune alle diverse aree
scientifiche dell’ingegneria e della fisica.
Gli studi e i risultati ottenibili in un settore diventano
spendibili nelle descrizioni di fenomeni fisici in
termini di campi, che presentino forti analogie ed in
particolare nel fenomeno della trasmissione del
calore.
M. Usai
Ingegneria dei Sistemi Elettrici_2b
50