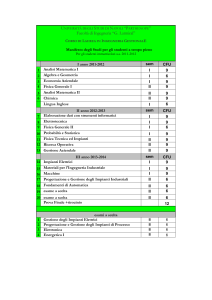
Potenza volumica. Legge di Joule in forma locale
Si consideri un tubo di flusso elementare all’interno di un corpo
conduttore nel quale ha sede un campo di corrente.
E
P
J
dA
n
dl
V
V-dV
La potenza elettrica che fluisce nel bipolo infinitesimo è:
⎧dV = -E ⋅ dl
dP = −dV ⋅ dI ed essendo ⎨
⎩dI = J ⋅ dA
dP = E ⋅ J dl dA = E ⋅ J dVol
con dl dA = dVol volume del cilindretto infinitesimo.
M. Usai
Ingegneria dei Sistemi Elettrici_4b
1
La potenza volumica, ossia la potenza assorbita per unità di
volume:
p = EJ = ρ J 2 = γE 2
(essendo: dP = E ⋅ J dl dA = E ⋅ J dVol = p dVol )
che esprime la legge di Joule in forma locale
I materiali passivi in regime stazionario si classificano in
dielettrici, isolanti e semiconduttori.
I materiali conduttori sono quelli con ρ < 2 µΩm
e ρ(θ) é legata alla temperatura da una legge empirica:
ρ
2
ρ rame = 0,0175
Ω ⋅ mm
m
ρ(θo)
θ1
M. Usai
θ1- θ0
θ0
Ingegneria dei Sistemi Elettrici_4b
θ
2
Se ρ(θ0 ) è la resistività alla temperatura θ0 di riferimento.
ρ alla temperatura θ è ricavabile da una relazione approssimata
lineare:
ρ ( θ ) = ρ ( θ 0 ) ⎡⎣1 + α ( θ 0 ) ⋅ ( θ − θ 0 ) ⎤⎦
Essendo α (θ 0 ) il coefficiente di variazione della resistività in
funzione della temperatura (C-1)
M. Usai
Ingegneria dei Sistemi Elettrici_4b
3
Metodo generale per la determinazione della resistenza di un conduttore di forma qualsiasi:
1.
Scelta del sistema di coordinate
2.
Definizione della geometria delle superfici
orientate A, attraversate dalla corrente elettrica
I,in funzione del sistema di riferimento scelto.
a)
Calcolo della densità di corrente J in funzione
della corrente elettrica I
b) Calcolo del campo elettrico E in funzione della
densità di corrente J:
c)
Calcolo della differenza di potenziale in
funzione del campo
⎛ dI ⎞ dI
J=⎜
n
⎟=
⎝ d A ⎠ dA
E = J /γ = ρ J
d) Calcolo della resistenza elettrica:
M. Usai
l2
U1 − U 2 = ∫1 E ⋅ dl
Ingegneria dei Sistemi Elettrici_4b
1
U1 -U 2
R=
I
4
Esempi di campi di corrente
a) Campo di corrente uniforme all’interno di un tubo cilindrico
conduttore.
l
dA
E
J
d
P
I
+
U
Si suppone l >> d;
•che il materiale del tubo sia omogeneo isotropo e passivo e;
•che il tubo sia circondato da materiale di resistività infinita.
M. Usai
Ingegneria dei Sistemi Elettrici_4b
5
Con queste ipotesi:
• le linee di forza risultano parallele all’asse del cilindro e
• le superfici equipotenziali sono perpendicolari ad esse.
Il campo e la densità di corrente risultano indipendenti dal punto,
per cui si può scrivere
U El
l
U = E ⋅l I = J ⋅ A ⇒ R = =
=ρ
I JA
A
R= ρ
l
A
relazione valida per i conduttori filiformi.
M. Usai
Ingegneria dei Sistemi Elettrici_4b
6
b) Campo di corrente cilindrico
Si considerino due conduttori perfetti cilindrici coassiali di raggi
r1 ed r2 separati da un mezzo isolante.
l
r2
r
+
P
J
E
r1
U
In queste condizioni se si applica una differenza di potenziale tra
le due armature si genera un campo radiale.
M. Usai
Ingegneria dei Sistemi Elettrici_4b
7
In ciascun punto del materiale isolante si può scrivere:
J = γ ⋅ E e J = γ E con J =
I
2πrl
e per l = 1
I
J=
⇒ E=
2π r
γ2πr
I
r2
r2
1
1
U1 − U 2 = ∫r E dr = ∫r
I
I
r2
dr =
ln
γ2πr
2πγ r1
U1 -U 2
r2
l
R=
=
ln
I
2πγ r1
Questa è l’espressione della resistenza di isolamento dei cavi
coassiali
M. Usai
Ingegneria dei Sistemi Elettrici_4b
8
c) Campo di corrente sferico
r2
r
+
P
J
E
r1
U
Se il mezzo interposto tra due sfere è isotropo-omogeneo e le
superfici metalliche equipotenziali, il campo tra le due sfere è
radiale e se U1 > U2 , il fasore densità di corrente J è rivolto
verso l’esterno. Per una generica sfera di raggio r con r1 < r < r2
la densità di corrente relativa è:
I
J=
4π r 2
M. Usai
Ingegneria dei Sistemi Elettrici_4b
9
Per la legge di Ohm generalizzata:
E = ρ J ⇒ E = ρJ avendo E e J la stessa direzione e verso
l
I
essendo ρ =
E = ρJ =
2
γ4πr
γ
La differenza di potenziale tra i due elettrodi sarà:
r2
U 1 − U 2 = ∫ Edr =
r1
I
4πγ
⎛1 1⎞
I ⎛
r ⎞
⎜1− 1 ⎟
⎜ − ⎟=
r2 ⎠
⎝ r1 r2 ⎠ 4πγr1 ⎝
Per il calcolo della resistenza di terra si suppone r2 >> r1:
U l2
l ⎛1 1⎞
=
Rt =
⎜ − ⎟ e per r2 >> r1
I 4πγ ⎝ r1 r2 ⎠
M. Usai
Ingegneria dei Sistemi Elettrici_4b
Rt =
1
4πγ r1
10
Il potenziale di una sfera concentrica di raggio r > r1 sarà:
I
U r = U1 −
4πγ
U1 =
⎛ 1 1⎞
⎜⎜ − ⎟⎟
⎝ r1 r ⎠
I
4πγr1
o
M. Usai
⎧
⎛ I ⎞
⎪ per r = r1 ⇒ U r = ⎜ 4πγ r ⎟ = U 1
⎪
⎝
1⎠
⎨
⎪ per r = ∞ ⇒ U = U − I = 0
r
1
⎪⎩
4πγ r1
r1
=1
r1
Ingegneria dei Sistemi Elettrici_4b
r
=1
r1
11
Per un dispersore semisferico:
I ⎛ 1 1⎞
⎜ − ⎟
2πγ ⎝ r1 r ⎠
I
Rt =
2πγ r1
U lr =
La resistenza di terra risulta doppia.
M. Usai
Ingegneria dei Sistemi Elettrici_4b
12
Con riferimento ai campi di corrente creati da dispersioni di
corrente sul terreno le norme CEI definiscono:
Tensione di passo: la tensione che, durante il funzionamento
di un impianto di terra, può risultare applicata tra i piedi di una
persona a distanza di passo fissata convenzionalmente uguale
ad 1 m.
Tensione di contatto: la tensione alla quale può essere
soggetto a corpo umano in seguito a contatto con carcasse e
strutture metalliche delle macchine o apparecchiature,
normalmente non in tensione.
M. Usai
Ingegneria dei Sistemi Elettrici_4b
13