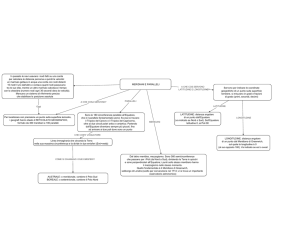
Una nuova geometria:
Un viaggio virtuale
sulla superficie sferica
Polo ed Equatore
Polo ed Equatore
Ogni retta (cerchio
massimo), ha due
centri sulla sfera
detti punti polari o
più semplicemente
poli della retta.
Ogni punto sulla sfera lo possiamo pensare come un
polo, pertanto per ogni punto potremo costruire uno e
uno solo cerchio massimo chiamato equatore.
1
Polo ed Equatore
L’idea corretta di polo ed equatore è proprio quella
che abbiamo dalla geografia:
L'equatore è la circonferenza massima
della superficie di un corpo celeste
(approssimativamente
sferico)
perpendicolare all'asse di rotazione e
quindi equidistante dai poli. La latitudine
dell'equatore è, per definizione, pari a 0
quindi non ha senso, se ci si trova in
corrispondenza dell' equatore, parlare di
latitudine Nord o Sud. L'equatore divide
un corpo celeste in due emisferi
comunemente
detti
emisfero
settentrionale e meridionale.
Polo ed Equatore
PROBLEMA:
Come possiamo
costruire i poli di
un dato cerchio
massimo sul quale
giacciono due
punti A e B (dato
quindi un
equatore)?
2
Polo ed Equatore
Dati i due punti
posso costruire la
retta a (ossia il
cerchio massimo)
passante per i due
punti A e B.
Polo ed Equatore
Traccio quindi la
retta
perpendicolare b
alla retta a appena
costruita e
passante per il
punto A.
3
Polo ed Equatore
Eseguo lo stesso
procedimento per il
punto B e
l’intersezione delle
due rette
perpendicolari b e c
ad a appena
costruite, sarà
proprio il polo
dell’equatore
passante per a e b.
Polo ed Equatore
Osservazione:
Tutte le rette
passanti per il polo
formano angoli retti
quando intersecano il
rispettivo l’equatore.
4




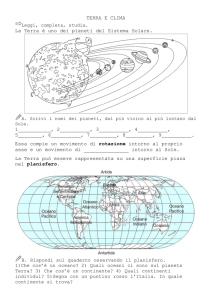
![reticolato geografico[1].D20a](http://s1.studylibit.com/store/data/001724247_1-5bb062e1e71aac389a17cb5e10e7351d-300x300.png)