ELETTROTECNICA
2 Test in itinere del 11/01/2006
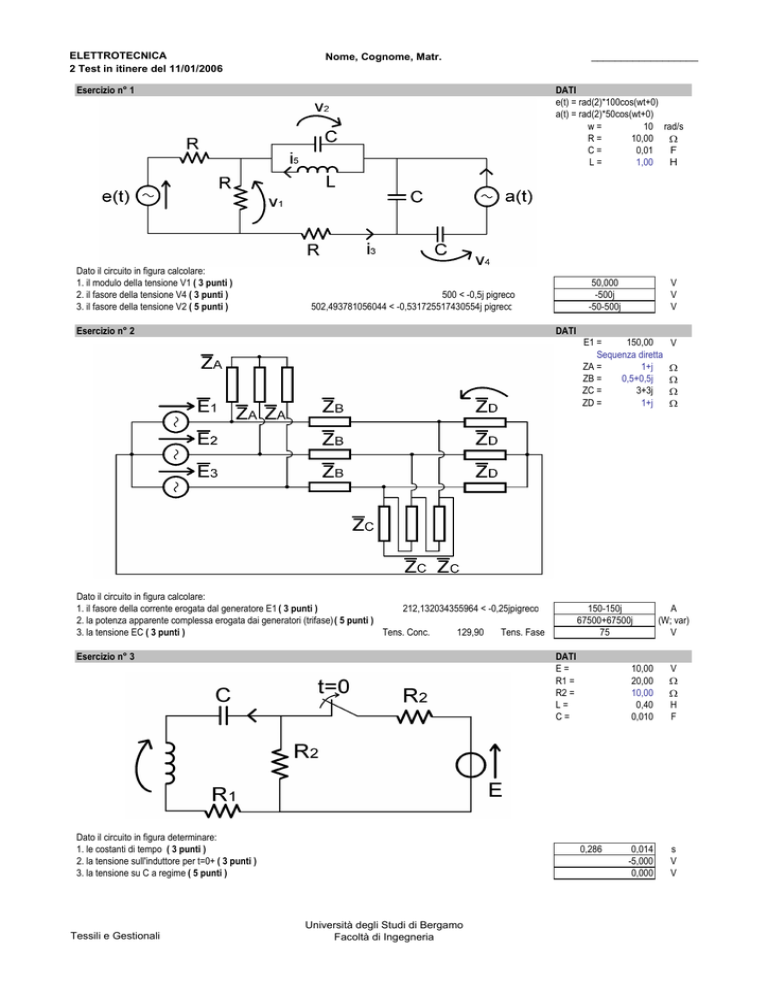
Esercizio n° 1
Dato il circuito in figura calcolare:
1. il modulo della tensione V1 ( 3 punti )
2. il fasore della tensione V4 ( 3 punti )
3. il fasore della tensione V2 ( 5 punti )
__________________
Nome, Cognome, Matr.
DATI
e(t) = rad(2)*100cos(wt+0)
a(t) = rad(2)*50cos(wt+0)
w=
10 rad/s
R=
10,00
Ω
F
C=
0,01
H
L=
1,00
50,000
-500j
-50-500j
500 < -0,5j pigreco
502,493781056044 < -0,531725517430554j pigreco
Esercizio n° 2
V
V
V
DATI
E1 =
150,00
Sequenza diretta
ZA =
1+j
ZB =
0,5+0,5j
ZC =
3+3j
ZD =
1+j
Dato il circuito in figura calcolare:
212,132034355964 < -0,25jpigreco
1. il fasore della corrente erogata dal generatore E1 ( 3 punti )
2. la potenza apparente complessa erogata dai generatori (trifase) ( 5 punti )
3. la tensione EC ( 3 punti )
Tens. Conc.
129,90
Tens. Fase
Esercizio n° 3
DATI
E=
R1 =
R2 =
L=
C=
Dato il circuito in figura determinare:
1. le costanti di tempo ( 3 punti )
2. la tensione sull'induttore per t=0+ ( 3 punti )
3. la tensione su C a regime ( 5 punti )
Tessili e Gestionali
150-150j
67500+67500j
75
0,286
Università degli Studi di Bergamo
Facoltà di Ingegneria
V
Ω
Ω
Ω
Ω
A
(W; var)
V
10,00
20,00
10,00
0,40
0,010
V
Ω
Ω
H
F
0,014
-5,000
0,000
s
V
V
ELETTROTECNICA
2 Test in itinere del 11/01/2006
Esercizio n° 1
Dato il circuito in figura calcolare:
1. il modulo della tensione V1 ( 3 punti )
2. il fasore della tensione V4 ( 3 punti )
3. il fasore della tensione V2 ( 5 punti )
__________________
Nome, Cognome, Matr.
DATI
e(t) = rad(2)*100cos(wt+0)
a(t) = rad(2)*50cos(wt+0)
w=
10 rad/s
R=
20,00
Ω
F
C=
0,02
H
L=
0,50
50,000
-250j
-50-250j
250 < -0,5j pigreco
254,950975679639 < -0,562832958189001j pigreco
Esercizio n° 2
V
V
V
DATI
E1 =
200,00
Sequenza inversa
ZA =
3+j
ZB =
1,5+0,5j
ZC =
9+3j
ZD =
3+j
Dato il circuito in figura calcolare:
126,491106406735 < -0,102416382349567jpig
1. il fasore della corrente erogata dal generatore E1 ( 3 punti )
2. la potenza apparente complessa erogata dai generatori (trifase) ( 5 punti )
3. la tensione ED ( 3 punti )
Tens. Conc.
173,21
Tens. Fase
Esercizio n° 3
DATI
E=
R1 =
R2 =
L=
C=
Dato il circuito in figura determinare:
1. le costanti di tempo ( 3 punti )
2. la tensione sull'induttore per t=0+ ( 3 punti )
3. la tensione su C a regime ( 5 punti )
Tessili e Gestionali
120-40j
72000+24000j
100
0,439
Università degli Studi di Bergamo
Facoltà di Ingegneria
V
Ω
Ω
Ω
Ω
A
(W; var)
V
10,00
30,00
15,00
0,50
0,010
V
Ω
Ω
H
F
0,011
-5,000
0,000
s
V
V
ELETTROTECNICA
2 Test in itinere del 11/01/2006
Nome, Cognome, Matr.
Esercizio n° 1
Dato il circuito in figura calcolare:
1. il modulo della tensione V1 ( 3 punti )
2. il fasore della tensione V4 ( 3 punti )
3. il fasore della tensione V2 ( 5 punti )
__________________
DATI
e(t) = rad(2)*100cos(wt+0)
a(t) = rad(2)*50cos(wt+0)
w=
R=
C=
L=
50,000
-62,5j
-50-62,5j
62,5 < -0,5j pigreco
80,0390529679106 < -0,714776712522723j pigreco
Esercizio n° 2
20 rad/s
30,00
Ω
F
0,04
H
0,06
V
V
V
DATI
E1 =
200,00
Sequenza inversa
ZA =
3+3j
ZB =
1,5+1,5j
ZC =
9+9j
ZD =
3+3j
Dato il circuito in figura calcolare:
1. il fasore della corrente erogata dal generatore E1 ( 3 punti )
94,2809041582064 < -0,25jpigreco
2. la potenza apparente complessa erogata dai generatori (trifase)( 5 punti )
3. la tensione ED ( 3 punti )
Tens. Conc.
173,21
Tens. Fase
Esercizio n° 3
Tessili e Gestionali
1,483
Università degli Studi di Bergamo
Facoltà di Ingegneria
Ω
Ω
Ω
Ω
66,6666666666667-66,6666666666667j
A
40000+40000j
(W; var)
100
V
DATI
E=
R1 =
R2 =
L=
C=
Dato il circuito in figura determinare:
1. le costanti di tempo ( 3 punti )
2. la tensione sull'induttore per t=0+ ( 3 punti )
3. la tensione su C a regime ( 5 punti )
V
100,00
20,00
10,00
0,50
0,050
V
Ω
Ω
H
F
0,017
-50,000
0,000
s
V
V
ELETTROTECNICA
2 Test in itinere del 11/01/2006
Nome, Cognome, Matr.
Esercizio n° 1
Dato il circuito in figura calcolare:
1. il modulo della tensione V1 ( 3 punti )
2. il fasore della tensione V4 ( 3 punti )
3. il fasore della tensione V2 ( 5 punti )
__________________
DATI
e(t) = rad(2)*100cos(wt+0)
a(t) = rad(2)*50cos(wt+0)
w=
R=
C=
L=
rad/s
Ω
F
H
50,000
-31,25j
-50-31,25j
31,25 < -0,5j pigreco
58,9623820753538 < -0,822192315510647j pigreco
Esercizio n° 2
40
40,00
0,04
0,02
V
V
V
DATI
E1 =
230,00
Sequenza inversa
ZA =
2+3j
ZB =
1+1,5j
ZC =
6+9j
ZD =
2+3j
Dato il circuito in figura calcolare:
1. il fasore della corrente erogata dal generatore E1 ( 3 punti )
127,581045131803 < -0,312832958189001jpigreco
2. la potenza apparente complessa erogata dai generatori (trifase) ( 5 punti )
3. la tensione ED ( 3 punti )
Tens. Conc.
199,19
Tens. Fase
Esercizio n° 3
DATI
E=
R1 =
R2 =
L=
C=
Dato il circuito in figura determinare:
1. le costanti di tempo ( 3 punti )
2. la tensione sull'induttore per t=0+ ( 3 punti )
3. la tensione su C a regime ( 5 punti )
Tessili e Gestionali
70,7692307692308-106,153846153846j
48830,7692307693+73246,1538461537j
115
0,252
Università degli Studi di Bergamo
Facoltà di Ingegneria
V
Ω
Ω
Ω
Ω
A
(W; var)
V
200,00
10,00
5,00
0,60
0,020
V
Ω
Ω
H
F
0,048
-100,000
0,000
s
V
V
ELETTROTECNICA
2 Test in itinere del 11/01/2006
Esercizio n° 1
Dato il circuito in figura calcolare:
1. il modulo della tensione V1 ( 3 punti )
2. il fasore della tensione V4 ( 3 punti )
3. il fasore della tensione V2 ( 5 punti )
__________________
Nome, Cognome, Matr.
DATI
e(t) = rad(2)*100cos(wt+0)
a(t) = rad(2)*50cos(wt+0)
w=
10 rad/s
R=
50,00
Ω
F
C=
0,04
H
L=
0,25
50,000
-125j
-50-125j
125 < -0,5j pigreco
134,629120178363 < -0,621118941590843j pigreco
Esercizio n° 2
V
V
V
DATI
E1 =
110,00
Sequenza inversa
ZA =
2+2j
ZB =
1+j
ZC =
6+6j
ZD =
2+2j
Dato il circuito in figura calcolare:
77,7817459305202 < -0,25jpigreco
1. il fasore della corrente erogata dal generatore E1 ( 3 punti )
2. la potenza apparente complessa erogata dai generatori (trifase) ( 5 punti )
3. la tensione ED ( 3 punti )
Tens. Conc.
95,26
Tens. Fase
Esercizio n° 3
DATI
E=
R1 =
R2 =
L=
C=
Dato il circuito in figura determinare:
1. le costanti di tempo ( 3 punti )
2. la tensione sull'induttore per t=0+ ( 3 punti )
3. la tensione su C a regime ( 5 punti )
Tessili e Gestionali
55-55j
18150+18150j
55
1,190
Università degli Studi di Bergamo
Facoltà di Ingegneria
V
Ω
Ω
Ω
Ω
A
(W; var)
V
100,00
40,00
20,00
0,60
0,020
V
Ω
Ω
H
F
0,010
-50,000
0,000
s
V
V
ELETTROTECNICA
2 Test in itinere del 11/01/2006
Esercizio n° 1
Dato il circuito in figura calcolare:
1. il modulo della tensione V1 ( 3 punti )
2. il fasore della tensione V4 ( 3 punti )
3. il fasore della tensione V2 ( 5 punti )
__________________
Nome, Cognome, Matr.
DATI
e(t) = rad(2)*50cos(wt+0)
a(t) = rad(2)*100cos(wt+0)
w=
10 rad/s
R=
60,00
Ω
F
C=
0,05
H
L=
0,20
Esercizio n° 2
V
V
V
25,000
-200j
-25-200j
200 < -0,5j pigreco
201,556443707464 < -0,539583424160566j pigreco
DATI
E1 =
1000,00
Sequenza inversa
ZA =
1+2j
ZB =
0,5+j
ZC =
3+6j
ZD =
1+2j
Dato il circuito in figura calcolare:
1. il fasore della corrente erogata dal generatore E1 ( 3 punti )
894,427190999916 < -0,352416382349567jpigreco
2. la potenza apparente complessa erogata dai generatori (trifase) ( 5 punti )
3. la tensione ED ( 3 punti )
Tens. Conc.
866,03
Tens. Fase
Esercizio n° 3
DATI
E=
R1 =
R2 =
L=
C=
Dato il circuito in figura determinare:
1. le costanti di tempo ( 3 punti )
2. la tensione sull'induttore per t=0+ ( 3 punti )
3. la tensione su C a regime ( 5 punti )
Tessili e Gestionali
400-800j
1200000+2400000j
500
1,180
Università degli Studi di Bergamo
Facoltà di Ingegneria
V
Ω
Ω
Ω
Ω
A
(W; var)
V
50,00
20,00
10,00
0,60
0,040
V
Ω
Ω
H
F
0,020
-25,000
0,000
s
V
V










