Le forze in gioco
Prima di parlare direttamente di quali sono le forze in gioco in una nanostruttura è meglio
descrivere esempi di oggetti che possono essere ottenuti in laboratorio e di quelli con cui si è già in
contatto nella vita di tutti i giorni.
Un modo per ottenere un nano-cristallo è quello di avere a disposizione il materiale di base in una
soluzione diluita. Successivamente si aumenta la temperatura della soluzione in modo tale che le
molecole si muovano e formino per collisione i primi germi di aggregazione del cristallo 3D. In
ultimo si blocca il processo allo stadio “nano” e si isolano i nanocristalli. Un esempio di questo
avviene con catene polimeriche in soluzione con le quali si possono formare nano-micelle nei loro
punti di contatto creatisi per agitazione termica.
micelle
Un altro esempio di formazione di nano strutture è l’HBC. Questo composto, formato
dall’autoaggregazione di più molecole di HBC impilate una sull’altra, si è dimostrato un ottimo
conduttore di corrente. Infatti, applicando un campo elettrico con l’uso di due elettrodi sulla
soluzione contenente HBC si formano nano-fili conduttori orientati secondo la polarità del campo.
Più vicino all’esperienza quotidiana è invece il caso dei cristalli liquidi. Le loro molecole sono
costituite da 2 anelli benzenici (sui quali si forma un dipolo elettrico) ed da una lunga coda
costituita da gruppi CH2. Questi composti sono lineari e in grado di disporsi parallelamente gli uni
agli altri, alternando la posizione della testa e della coda di molecole adiacenti. Ad alte temperature
la catena dei CH2 è in grado di disporsi linearmente nello spazio mantenendo le molecole vicine fra
loro e conferendo colore “scuro” al materiale; mentre a quelle basse le code si arrotolano su se
stesse, distanziano le molecole e rendono il materiale trasparente. Questo switch (coloretrasparenza) avviene in brevissimo tempo e con l’applicazione di un bassissimo voltaggio
(nell’ordine dei milionesimi di Volt) altrimenti, ad esempio, la pila degli orologi si esaurirebbe in
pochi secondi.
Alta T
Bassa T
code
Oggetto di interesse e di studio per i nanomateriali sono soltanto i cristalli e i cristalli liquidi per cui
le forze in gioco ricadono nella tipologia dei solidi.
Consideriamo l’interazione fra due atomi, anche perchè l’estensione al caso pluriatomico e solo un
problema di calcolo risolvibile con un qualsiasi computer.
La forza F di interazione atomo-atomo dipende dalla distanza alla quale essi si trovano e verrà
descritta dalla derivata di una funzione potenziale V supposta nota:
F(r)= - dV/dr
dove di V si conosce solo l’andamento qualitativo della parte attrattiva e repulsiva, l’re, il punto di
minimo e il delta di dissociazione.
La curva V può essere descritta solo da modelli che ne approssimano l’andamento qualitativo che a
sua volta è stato dedotto dalla proprietà delle dilatazione dei corpi all’aumentare dell’energia.
Infatti, se si incrementa il valore di E sulla curva V rispetto al minimo, il sistema oscilla tra due
punti distinti, ma il punto medio di equilibrio di tale oscillazione si sposta verso destra. In termini
fisici significa che il contributo repulsivo diventa più forte dell’attrattivo.
V
r’eq
r
Delta E
req
L’estensione di V al caso pluriatomico in formula è:
V=∑ V(rij)
Il modello più usato per l’approssimazione della curva V è quello di Lenner-Jones:
V(r) = 4ε[σ/r12 – σ/r6]
Dove ε e σ sono dati noti in funzione dei due atomi considerati. Trattandosi di un modello ci sono
casi in cui la formulazione viene limitatamente rimaneggiata e corretta soprattutto nei due esponenti
di r allo scopo di meglio adattarla al singolo caso.
Nell’interazione atomo-atomo oltre a Lenner-Jones c’è da tener conto anche di un contributo
elettrostatico descritto da Stockmayer. Nella formulazione generale quindi le interazioni atomoatomo vengono descritte da LJ+elettr.
È necessario fare una considerazione anche sul raggio di azione delle diverse forze presenti e,
quando possibile, fornire per ognuna di esse una formulazione matematica.
Le forze a short-range sono quelle che agiscono tra atomi vicini e alla distanza di 2 o 3 unità non
vengono più percepite.
• Forze di valenza: sono forze di legame chimico, valgono 300 kcal /mol. Non vengono
percepite dal secondo atomo vicino a meno che non vi sia la presenza di due doppi legami
consecutivi con elettroni π.
Le forze a long-range vengono percepite anche a 30-40 unità di distanza.
• Interazioni elettrostatiche fra cariche supposta puntiformi:
Vab=(Ca Cb)/r, dove C sono le cariche.
• Interazioni carica-dipolo
Vab= - (Ca µb)/r2 cos θ, dove C è la carica e µ il dipolo.
• Interazione dipolo-dipolo
Vab= - (µa µb)/r3 GF, dove µ sono i dipoli.
• Interazione dipolo indotto-dipolo indotto
Sono le forze di dispersione di Van der Walls, valgono 0,5- 2 Kcal/mole.
• Forze di polarizzazione
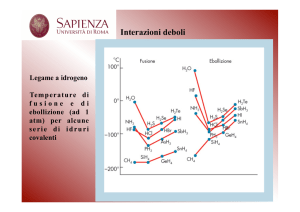
Sono i legami H, valgono 7-10 kcal/mole.