Cariche in movimento.Corrente elettrica.
Correnti elettriche: cariche che si muovono in un mezzo conduttore quando in
esso viene mantenuto un campo Elettrico per esempio se viene connesso tra i poli
di una batteria.
Correnti continue cc: vengono prodotte da batterie o generatori che forniscono
una ddp unidirezionale costante tra i poli e convertono energia chimica,
meccanica o di altro tipo in energia elettrica
Correnti alternate ca: vengono prodotte da generatori che hanno tra i poli una ddp
che cambia segno ad una frequenza caratteristica (50Hz)
Corrente Elettrica: Flusso di carica attraverso una superficie
l
Grandezza fisica scalare
I =
I = dq/dt: corrente elettrica istantanea
!
!
"q
"t
[I ] =
C
=A
s
Corrente media
unità fondamentale SI
1
Punto di vista microscopico
l
n: numero di cariche e per unita di volume
A
ΔQ : carica totale mobile nel tratto l del
conduttore
ΔQ=nelA
I=
!
"Q nelA
=
= neAv d
"t l /v d
Δt: tempo necessario a ΔQ per attraversare la
sezione A
Δt=l/vd
vd : velocita` media con cui si
muovono i portatori di carica sotto
l’effetto del campo elettrico
vd :quanto vale?? vd =I/neA per un filo di rame n=8.5x 1028elettroni/m3 di
diametro d=2mm per una corrente I=10A
Confrontare il risultato con la velocita` media termica a temp. ambiente
vt≈105m/s
2
Esempio
Una cella elettrochimica è costituita da due elettrodi di
argento posti in una soluzione acquosa di nitrato
d’argento. Una corrente costante I=0.5A passa
attraverso la cella per un’ora. Calcolare:
a)
La carica totale che attraversa la cella in C e in
multipli di carica elettronica
Ciascun elettrone che raggiunge la cella neutralizza uno
ione d’argento carico positivamente che quindi si
deposita come argento metallico sull’elettrodo
negativo (catodo). Calcolare:
b) La massa totale dell’argento depositato. (massa
atomica dell’ Ag 107.9amu)
3
Generatori di tensione
Per mantenere una corrente serve un generatore: strumento che mantiene una d.d.p. (tensione)
costante ai suoi capi (f.e.m.)
A
ε
+
-
ΔV=VA-VB= ε
B
Circuito aperto: separa cariche positive e negative.
Compie lavoro contro il campo elettrico finché ddp=fem
A
Qui ci vuole
un “carico”
i
ε
Il verso convenzionale della
corrente è quello nel quale
si muoverebbero le cariche
positive
B
Circuito chiuso: le cariche portate da B ad A sono riportate da A a B dal campo elettrico.
Il generatore compie lavoro, finché non abbia esaurito la sua riserva di energia.
Potenza erogata da un generatore (lavoro compiuto/tempo):
d W = dq ! "V =
dW
P=
=
i
dt
#
#dq
4
Corrente elettrica
Per molti conduttori (es. conduttori metallici) vale la
Legge di Ohm
A
!V = Ri
ε
i
B
ΔV=VA-VB
[R]= V
A
=
kg m 2
=!
A2 s 3
ddp o “caduta di tensione” ai capi di un resistore.
Rappresentazione schematica
di un resistore di resistenza R
R
i
123
ΔV=Ri
La resistenza dipende dal materiale e dalla geometria. Per un filo di lunghezza l e sezione S:
R=!
l
S
ρ resistività: dipende solo dal materiale (e dalla temperatura)
[" ]= !m
5
Effetto Joule
A
Il circuito più semplice:
Generatore ideale
! = V = Ri
ε
R
B
Da A a B il campo elettrico compie un lavoro -qΔV >0.
La velocità di deriva non cambia (legge di Ohm): dissipazione
di energia.
Ltot = "q#V + Ld = #K = 0
Ld = q#V
i
PDISS = i!V = i " Ri = Ri
2
V2
=
R
Generatore reale
!
La ddp ai capi di un generatore con circuito aperto (detta
anche f.e.m), è diversa (maggiore) dalla ddp con circuito
chiuso. Ciò è dovuto alla resistenza interna del generatore:
A
"V = # ! ri i
ε
ri
B
R
i
ri è responsabile del
riscaldamento del generatore
6
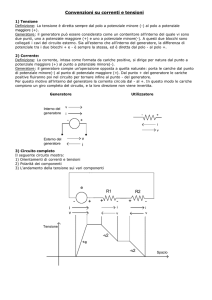
Circuiti elettrici
Simbologia
condensatore
resistore
generatore ideale di tensione
generatore di tensione reale
ε
R1
R3
R2
nodo
maglia (ma non solo)
Legge di Kirchoff dei nodi:
!i
Legge di Kirchoff delle maglie:
# !V = #" + # R i
k
=0
k
k
k
k
k
k k
=0
m
7
Serie e parallelo di resistenze
i
R1
R2
V = V1 + V2 = ( R1 + R2 ) i
V = Reqi ! Req = R1 + R2
REQ = ! Rk
k
i1
R1
R2
i2
Resistenze in serie
Vk = Rk ik = V
i = ! ik "
k
1
1
=!
Req
k Rk
Resistenze in parallelo
8
Circuito RC
R
Inizio:
C
ε
i =0
Q = 0 ! VC = 0
U=0
R
Fine:
i =0
C
ε
VC = ! " Q = C!
1
U = C! 2
2
C si è caricato: è passata corrente.
C possiede energia potenziale: è stato compiuto lavoro.
!
Q =
"
i (t )dt
0
Studio del regime transitorio
!
1
Q!
2
WG = Q
U =
Dov’è finita l’energia
mancante?
9
Circuito RC
R
i
ε
L. Kirchoff maglie:
C
con
Q !
+
RC R
!
i ( 0) =
Q(0) = 0
i="
Q
"
= Ri +
$
C
#
dQ
$i =
%
dt
!
R
di
i
=!
dt
RC
derivando ...
?
i = i0 exp(!t / RC ) =
" exp(!t / RC )
R
Q(t ) = " C [1 ! exp(! t / RC )]
i
!
R
RC: tempo caratteristico
!
eR
RC
t
10
Circuito RC
i
ε
R
Carica di un condensatore
C
i
Q
εC
t
VR ! i
t
VC ! Q
Dissipazione per effetto Joule
t
"
0
Ri 2 dt =
1
2
!C
#
WG = U C + WJ
11
Circuito RC
Scarica di un condensatore
i
R
!0 = Ri + Q
#
C
"
dQ
#i =
$
dt
C
ε
con
i (0) =
Q ( 0) = Q 0
|i|
Q0
V0
=
RC
R
Q
t
t
12
Alcuni Esempi:
L’Electrophorus:un pesce che vive nei fiumi dell’America del Sud ha un potente generatore
fisiologico di fem. Uccide i pesci di cui si nutre con potenti scariche di corrente fino a 1A.
Produce infatti una ddp di parecchie centinaia di Volts lungo la sua lunghezza , la corrente
passa dalla sua testa alla coda attraverso l’acqua.
Shock elettrico: una corrente elettrica che attraversa il corpo produce diversi effetti a
seconda dell’intensita` . La corrente dipende dalla ΔV e dalla resistenza R che attraversa.
Possiamo distinguere i seguenti casi:
Corrente Elettrica
(1 sec di contatto)
1mA
10-20 mA
100-300mA
Effetto Fisiologico
Soglia di percezione
Senzazione di formicolio
Sostenute contrazioni muscolari
Corrente che impedisce il distacco
Fibrillazione ventricolare, può essere
fatale se prolungata nel tempo
13
Perche` gli uccellini possono appoggiarsi sui fili dell’alta tensione senza danno?
Se inseriamo le dita nelle prese di casa 220V si possono evitare seri danni se
abbiamo scarpe con suola isolante che impedisce quindi alla corrente di
attraversare il nostro corpo con bassa resistenza
Infatti:
Se il nostro corpo oppone una resistenza di 100kΩ allora saremmo
attraversati da una corrente
I=220V/100kΩ = 2.2mA che produce solo una senzazione di formicolio
Ma se siamo sudati e a piedi scalzi la nostra resistenza verso massa potrebbe
essere di soli 1000Ω che significa
I=220V/1000Ω= 220mA che produce fibrillazione ventricolare e può essere
fatale
14
Corrente
(1 secondo di
contatto)
Effetti Fisiologici
Voltaggio richiesto per
produrre la corrente con
una resistenza corporea
di:
100kΩ
1kΩ
1mA
Soglia di percezione
Senzazione di formicolio
100V
1V
5mA
Corrente massima che non produce
dolore
500V
5V
10-20mA
Inizio di sostenute contrazioni
muscolari (“can’t let go” current)
1kV
10V
100-300mA
Fibrillazione ventricolare, fatale se
continuata nel tempo. La funzione
respiratoria continua
10kV
100V
6A
Sostenuta contrazione ventricolare
seguita da un normale ritmo
cardiaco (defibrillazione).
Temporanea paralisi respiratoria e
possibili bruciature
600kV
6kV
15