Le principali proprietà dei neutroni

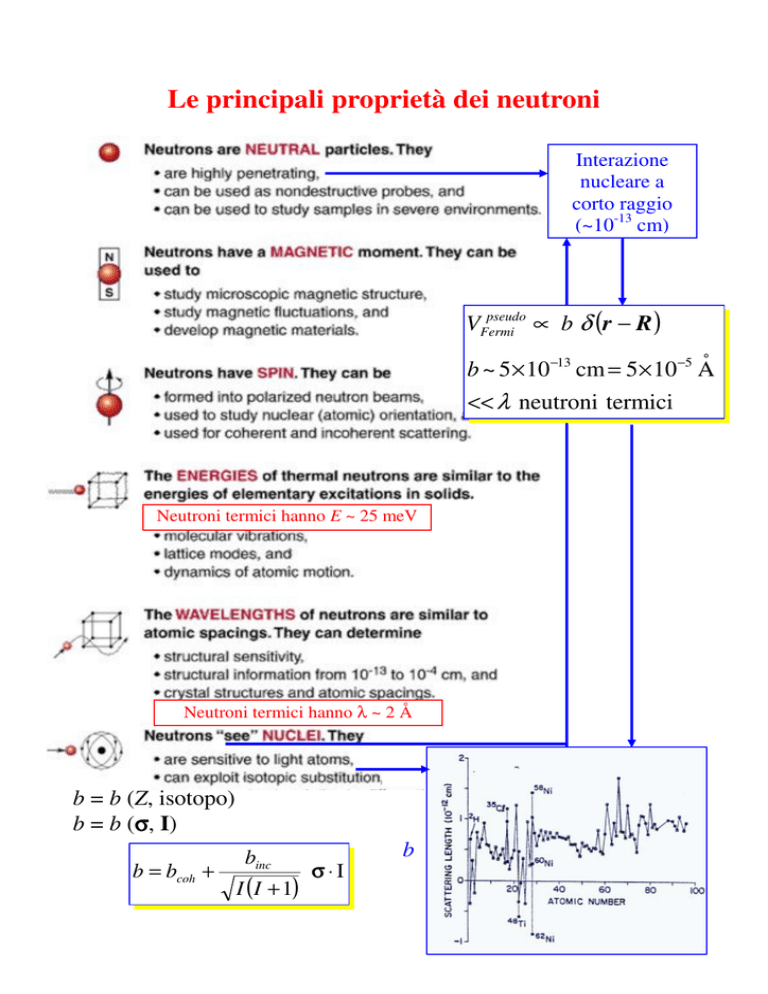
Le principali proprietà dei neutroni
Interazione
nucleare a
corto raggio
(~10-13 cm)
pseudo
VFermi
∝ b δ (r − R )
°
b ~ 5 × 10 −13 cm = 5 × 10 −5 A
<< λ neutroni termici
Neutroni termici hanno E ~ 25 meV
Neutroni termici hanno λ ~ 2 Å
b = b (Z, isotopo)
b = b (σ
σ, I)
b = bcoh +
binc
I (I + 1)
σ⋅I
b
Anticipando qualcosa sullo scattering
coerente e incoerente
G (r , t ) = Gd (r , t ) + Gs (r , t )
1
S (Q ,ω ) =
2π
∫
∫
d t e− i ω t dr e iQ⋅r [G (r , t ) − ρ ]
3
S (Q ,ω ) = S d (Q ,ω ) + Ss (Q ,ω ) − ρ (2π ) δ (Q )δ (ω )
Lo scattering incoerente sonda esclusivamente la parte self di S(Q,ω)
Quello coerente è invece proporzionale alla S(Q,ω) complessiva.
Ciò è generalmente un problema, a meno che una delle due
componenti nello scattering (coh o incoh) non sia dominante.
Esempi:
Campione monoisotopico ma con
I = 0 (come 36Ar, 86Kr…) è
TOTALMENTE coerente
L’idrogeno (ma non il deuterio!) ha
bcoh << binc ed è quindi
PREVALENTEMENTE incoerente
Lo scattering incoerente è una peculiarità dei neutroni e in certi
casi rappresenta un vantaggio perché permette di misurare
Ss(Q,ω). Ci sono poi metodi che consentono di accedere
separatamente ai due contributi di S(Q,ω): sostituzione isotopica;
neutroni polarizzati
incoerente
sample
coerente
Vantaggi/svantaggi dei neutroni
6) Self structure-related properties are accessible (kinetic properties: momentum distribution, velocity correlations,…)
Il confronto con altre sonde (I)
Neutroni
Grandezza
E (meV)
T (K)
λ (Å)
k (Å-1)
v (m s-1)
X
Freddi
Termici
Caldi
Epitermici
1
12
9.0
0.7
440
25
290
1.8
3.5
2200
150
1740
0.7
9
5400
1000
12000
0.29
22
14000
2
Luce
(vis.)
12400000
2480
1
6.3
5000
0.00126
2
hk
1
2
E= mv =
2
2m
E=
λ = 2π k = h
hc
λ = 2π k =
E
2mE
hc
λ
= hck
Il confronto con altre sonde (II)
(as with neutrons)
0) Intrinsic unsuitability to studies on excitations (few tens of meV) in matter, overcome by new X-HRS
X-rays High Resolution
Spectrometers
∆E ~ 3 ÷ 5 meV
∆E / E ~ 10-6 – 10-7
5) NULL possibility of measuring Self structure-related properties
La tipica geometria dello scattering
k1
k0
θ
La sonda scambia, in generale, sia energia che impulso con il campione.
Conservazione dell’energia
Conservazione dell’impulso
E = E0 – E1 =
h2
=
k02 − k12
2m
(
)
energia scambiata
Q = k0 – k1
vettore d’onda scambiato
Scattering anelastico e elastico
Un evento di scattering caratterizzato da scambio di energia
(E ≠ 0) e impulso è detto ANELASTICO. Ciò significa che il
vettore d’onda k del neutrone cambia sia in modulo che in
direzione, a seguito del processo di diffusione.
Q
k1
k1
θ
θ
k0
k0
k0 > k1 ⇒ E0 > E1 ⇒ E > 0
il neutrone CEDE energia al campione
Q
k0 < k1 ⇒ E0 < E1 ⇒ E < 0
il neutrone ACQUISTA energia dal campione
Nel caso particolare in cui k cambia solo in direzione ma non in
modulo (cioè k0 = k1), l’energia scambiata è zero (E = 0) e l’evento
è detto ELASTICO.
k1
Qel
θ
θ
Qel = 2 k0 sin
2
k0
Regione cinematica accessibile
2
2
0
2
1
Q = k0 – k1 ⇒ Q = k + k − 2 k1 k0 cosθ ⇒
Q
=
k0
 ω 
1 + 1 −  − 2 cosθ
 ω0 
E
E
Limitazione matematica e fisica
, ω 0 = 0 e, dalla
h
h
ω 
2
2 
conservazione dell’energia, k1 = k 0  1 −  .
ω0 

dove ω =
Diversamente, per un’onda elettromagnetica
(fotoni: luce, raggi X ⇒E = h c k, ω = c k) :
ω
ω0
ω < ω0 !!
180°
Q k0

ω 
k1 = k 0  1 − 
ω0 

Q
=
k0
1−
30°
2

ω 
 − 2 cosθ
1 + 1 −
 ω0 

ω 
1 −

 ω0 
Come prima, ω < ω0 … ma solo per una limitazione fisica.
ω ω0
A ciascun angolo di scattering θ è associato
un set di valori di Q e ω determinato dalla
relazione scritta sopra.
Definizione fenomenologica delle sezioni d’urto differenziali
In generale, in un esperimento di scattering anelastico in cui un fascio di neutroni caratterizzato da un flusso Φ
uniforme incide su un campione di N atomi identici, l’intensità (numero di conteggi nell’unità di tempo) misurata
nell’intervallo di frequenza ∆ω da un rivelatore di efficienza ε che sottende l’angolo solido ∆Ω intorno alla
direzione Ω(θ,ϕ) è, di fatto, proporzionale alle quantità menzionate.
rivelatore
La costante di proporzionalità è la sezione d’urto
differenziale doppia ed è una proprietà del
campione in studio:
d 2σ
I (θ ,ω )
(θ ,ω ) =
d Ωdω
Φ N ε ∆Ω∆ω
neutroni diffusi
k1
k0
neutroni incidenti
campione
neutroni trasmessi
N
Il suo integrale su tutti i possibili valori di ω, ad
un k0 fissato e per un angolo θ fissato, è la
sezione d’urto differenziale:
dσ
(θ ) =
dΩ
ω0
∫
−∞
d σ
I (θ )
≈
dΩ dω
Φ N ε ∆Ω
2
dω
θ =cos tan te
La sezione d’urto di scattering totale è
σs = ∫
dσ
dΩ =
dΩ
∫∫
d 2σ
d Ω dω
d Ωdω
La sezione d’urto totale è
σt = σs +σa
scattering
assorbimento
Connessione fra sezioni d’urto differenziali e proprietà strutturali (I)
La sezione d’urto differenziale doppia misura la probabilità (per unità di tempo) di un qualsiasi
processo di scattering in cui il vettore d’onda neutronico subisce la transizione k0 → k1,
indipendentemente da Φ, dallo stato del sistema atomico e dallo stato di spin del neutrone,
rispettando la conservazione dell’energia.
Dalla teoria delle perturbazioni al primo ordine, si trova:
 d σ 
1  m

=


2
 d Ωd E  k 0 → k 1 N  2π h
2
2
 k1

 k0
∑p
λ0
ps0
λ0 s0
∑
2
k1 s1 λ 1 V k 0 s 0 λ 0
[
× δ E + Eλ 0 − Eλ1
]
λ1 s1
Potenziale di interazione neutrone-nucleo
(a corto range ~ 10-13 cm)
pseudo
∝
Inserendo allora lo pseudopotenziale di Fermi per un sistema di N atomi [ VFermi
∑b
α
δ (r − Rα ) ],
α
usando la rappresentazione integrale della δ e facendo il cambiamento di variabile E = hω , si
arriva a scrivere:
2
k1
d σ
1
=
dΩdω 2π N k 0
+∞
∫
−∞
dt e −iω t
∑
bα∗ bβ e −iQ⋅Rα (0 ) e
i Q ⋅ Rβ (t )
α ,β
∑p
λ 0 ,s0
λ0
ps0 λ 0 s0 bα∗ bβ e −iQ⋅ Rα (0 )e
iQ ⋅ R β (t )
λ 0 s0
Connessione fra sezioni d’urto differenziali e proprietà strutturali (II)
Avevamo trovato dalla teoria delle funzioni di correlazione
1
1
1
1
− i ω t F (Q ,t ) ≈
−iω t
(
)
(
)
ρ
ρ
t
=
0
t
t
,
ω
S (Q ) =
d e
d e
d t e− i ω t
−Q
Q
N
2π
2π
2π N
∫
∫
∫
∑
e −iQ⋅Rα (0 ) e
iQ⋅ Rβ (t )
α ,β
Adesso, dalla teoria dello scattering di neutroni, abbiamo:
1 k1
d 2σ
=
dΩdω 2π N k 0
+∞
∫
dt e −iω t
−∞
∑
bα∗ bβ e −iQ⋅Rα (0 ) e
α ,β
Si somigliano molto!!
k ~
d 2σ
= 1 S (Q ,ω )
dΩ dω k 0
~
S (Q ,ω ) =
1
2π N
+∞
∫
−∞
dt e −iω t
∑
bα∗ bβ e −iQ⋅Rα (0 ) e
i Q⋅ Rβ (t )
α ,β
Se la sonda che sto utilizzando (neutroni) non apparisse esplicitamente attraverso
le lunghezze di scattering, questo sarebbe il fattore di struttura dinamico
i Q ⋅ Rβ (t )
Connessione fra sezioni d’urto differenziali e proprietà strutturali (III)
Avevamo trovato dalla teoria delle funzioni di correlazione nel caso statico:
S (Q ) ≈
1
ρ −Q ρ Q
N
=
1
N
∑
e −iQ⋅Rα (0 ) e
iQ⋅Rβ ( 0 )
=
α ,β
∫ dω S (Q ,ω )
Q cos tan te
Adesso, dalla teoria dello scattering di neutroni, abbiamo:
dσ
=
dΩ
ω0
∫
ω0
2
d σ
dω
dΩ dω
−∞
θ =cos tan te
=
∫
k ~
dω 1 S (Q ,ω ) ≠
k0
−∞
θ =cos tan te
+∞
1
~
dω S (Q ,ω ) =
N
−∞
∫
∑
α ,β
Q =cos tan te
dσ
~
≠ S (Q )
dΩ
1
~
S (Q ) =
N
∑
bα∗ bβ e −iQ⋅Rα (0 ) e
i Q ⋅ Rβ ( 0 )
α ,β
Se la sonda che sto utilizzando (neutroni) non apparisse esplicitamente attraverso
le lunghezze di scattering, questo sarebbe il fattore di struttura statico
bα∗ bβ e −iQ⋅Rα (0 ) e
i Q⋅ Rβ (0 )
Al di là delle ulteriori difficoltà che si incontrano nel caso statico per
ottenere la relazione fra sezioni d’urto misurate e quantità strutturali, sia
nel caso statico che in quello dinamico si presenta il problema
~
S
comune di trovare la relazione che intercorre fra
eS.
Si ricorda che le lunghezze di scattering b dipendono
dall’orientazione relativa fra lo spin del nucleo e quello del
binc
neutrone, e dal particolare isotopo.
b = bcoh +
I (I + 1)
σ⋅I
Si assume:
• bα∗ bβ e −iQ⋅Rα (0 ) e iQ⋅Rβ (0 ) ≈ bα∗ bβ e −iQ⋅Rα (0 ) e iQ⋅Rβ (K)
•
che i possibili diversi valori delle lunghezze di scattering (a causa
dello stato di spin e/o della specie isotopica) siano distribuiti in
modo casuale fra i vari atomi
Si assume, di fatto, di avere a che fare con una distribuzione casuale di
spin e isotopi (assenza di correlazione fra le lunghezze di scattering
associate a siti diversi) e di utilizzare neutroni non polarizzati.
2
α≠β
= bα*
bβ = b * b = b
2
= bcoh +
binc
I (I + 1)
σ⋅I
2
= bcoh
*
bα bβ =
α=β
*
2
= bα
bα bβ = b
2
2
Parte uguale per tutti gli atomi.
Hanno importanza, allora, solo
le relazioni di fase fra le onde
scatterate
(posizioni
degli
atomi) e quindi la struttura. Per
questo è detta coerente.
2
= b =
binc
bcoh +
σ⋅I
I (I + 1)
2
+ δ αβ  b − b

2
2
2
= bcoh
+ binc
 = b 2 + δ b 2
αβ inc
 coh
L’incoerente nasce dalle fluttuazioni della lunghezza di
scattering attorno al valor medio. Tali fluttuazioni sono
dovute sia alla distribuzione degli isotopi (incoerenza
isotopica), sia alla orientazione degli spin nucleari rispetto
allo spin del neutrone (incoerenza di spin), e sono
distribuite casualmente. Non porta informazioni strutturali
Connessione fra sezioni d’urto differenziali e proprietà strutturali (IV)
~
2
S (Q ,ω ) = bcoh
+∞

dt e −iω t 
2π N −∞
 β ,α ≠ β
1
~
S (Q ,ω ) =
1
2π N
∑
∫
bα∗ bβ
α ≠β
e −iQ⋅Rα (0 ) e
i Q ⋅ Rβ (t )
−∞
∑
bα
2
α
+∞
∫
+

e −iQ⋅ Rα (0 ) e iQ⋅ Rα (t ) 

+∞
dt e −iω t
∑
e −iQ⋅Rα (0 ) e
i Q ⋅ Rβ (t )
(
2
2
+ bcoh
+ binc
α ,β ≠α
) 2π1N ∫ dt e
Sd(Q,ω)
−∞
−iω t
∑
e −iQ⋅Rα (0 ) e iQ⋅Rα (t )
α
Ss(Q,ω)
Alternativamente, dato che S(Q,ω) = Sd(Q,ω) + Ss(Q,ω), si ha:
2
2
~
b
+
b
,
ω
,
ω
S (Q ) = coh S (Q ) inc S s (Q ,ω )
Da cui anche:
2
2
~
b
+
b
S (Q ) = coh S (Q ) inc
Entrambi i contributi, coerente e
incoerente,
possono
portare
informazioni di interesse.
L’unica componente di interesse è lo
scattering coerente
Il problema del caso statico
dσ
=
dΩ
ω0
∫
ω0
2
d σ
dω
dΩ dω
−∞
θ =cos tan te
=
∫
k ~
dω 1 S (Q ,ω ) ≠
k0
−∞
θ =cos tan te
+∞
∫
~
~
2
2
dω S (Q ,ω ) ≡ S (Q ) = bcoh
S (Q ) + binc
−∞
Q =cos tan te
dσ
~
≠ S (Q ) perché dipende dalla dinamica del sistema, seppur attraverso un integrale.
dΩ
Per ciascun angolo di scattering θ, eventi di scattering con tutti i possibili valori dell’energia
scambiata contribuiscono al valore di dσ / dΩ ⇒ gli eventi anelastici influenzano la sezione d’urto
differenziale misurata.
Se fosse ω << ω0, si avrebbe
Q = k0

ω
1 + 1 −
 ω0

 − 2 cosθ

ω
θ
1−
→ 2k 0 sin = Qel
2
ω0

ω 
 → k 02
k12 = k 02  1 −
ω0 

Da cui:
 dσ 


=
 d Ω ω << ω0
∫
ω0
k1 ~
S (Q ,ω ) dω
k0
−∞
Q cos tan te =Qel
∫
ω0
~
−∞
θ cos tan te
∫
+∞
−∞
Q cos tan te = Qel
k1 = k 0
~
= S (Q )
Caso ideale in cui gli
eventi di scattering sono
tutti ELASTICI
Il problema del caso statico: correzione anelastica
Nel caso ideale in cui tutti gli eventi fossero, di fatto, elastici avremmo relazione diretta fra sezione
d’urto misurata e fattore di struttura statico.
Ma lo scattering da liquidi è in generale anelastico. Si deve allora trovare un modo per estrarre dalla
dσ / dΩ effettivamente misurata (e affetta dai processi anelastici) il comportamento limite (legato a S(Q)) che si
avrebbe se lo scattering fosse elastico. Tale procedura è nota come correzione anelastica.
Si può individuare immediatamente una correzione anelastica additiva come quella quantità per cui
la dσ / dΩ misurata differisce da (dσ / dΩ)ω << ω0, cioè:
Viene calcolata tramite l’uso di
modelli, ad esempio il gas perfetto
 dσ  dσ 
  dσ
~ 
(Q )
P=
−
=
−
S

 

 dΩ  dΩ ω << ω 0   dΩ
di modo che:
dσ
~
= S (Q ) + P
dΩ
1  dσ
⇒ S (Q ) = 2 
bcoh  dΩ
exp
2
inc
− P −b
calcolata



Pg . p .
 ω0
d 2σ
~ 

 dσ
= 
− S (Q ) = 
dω
dΩ dω
 dΩ
 g . p.  −∞
θ = cos tan te


=



k1 ~
~

S (Q ,ω )g . p . dω − S (Q ) g . p . 
k0
−∞

θ cos tan te

∫
∫
~
− S (Q )


 =

 g . p.
ω0
2
 Mβ 
1 Mβ
hQ 2  
2
2
2
2
~
ω −
 
exp −
S (Q ,ω )g . p . = bcoh + binc Ss (Q ,ω )g . p . = bcoh + binc
2 
Q 2π
2 M  
 2 Q 

(
)
σs
2
2
~
S (Q )g . p . = bcoh + binc =
4π
(
)
(
)