LAVORO ED ENERGIA
ESERCIZIO 1
Dato il campo di forze F = −α(3x2 î + 3z2 jˆ + 6yz k̂): a) determinare le dimensioni di α; b) essendo il campo conservativo con energia potenziale pari a U (x, y, z) = αx3 + 3αyz2 [posto U0 =
U (0, 0, 0) = 0], verificare che U ha le dimensioni di una energia; c) supponendo che α valga
2.5 nelle unità del SI, calcolare il lavoro compiuto dalla forza per portare un oggetto dal punto
A(1, 2, −1) al punto B(2, 1, 1). Si considerino le coordinate dei punti espresse in metri.
ESERCIZIO 2
Una sferetta di massa m = 0.5 kg è appesa all’estremità di un filo inestensibile di massa trascurabile
lungo l = 1 m fisso all’altro estremo. Soffia il vento in direzione orizzontale e la sfera inizialmente
in quiete sulla verticale si solleva fino a quando il filo forma con la verticale un angolo ϕ = 60 ◦ .
Calcolare: a) il lavoro compiuto dal vento; b) la tensione
della fune; c) la velocità v costante con
√
2
cui soffia il vento, sapendo che |F| = kv con k = 3 g/m.
ESERCIZIO 3
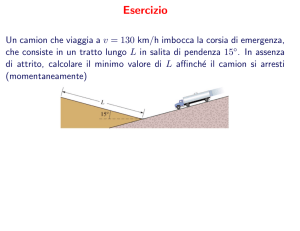
Un corpo di massa m si muove su un piano orizzontale scabro e all’istante iniziale ha velocità v 0 .
Dopo un tratto D il corpo comprime di un tratto l una molla ideale di costante elastica k e lunghezza
a riposo nulla fino a fermarsi. Calcolare il coefficiente d’attrito dinamico µ.
ESERCIZIO 4
Un profilo rigido è costituito da un tratto orizzontale OA, da un piano inclinato AB di altezza
h = 2.5 m, da una buca BC di lunghezza L = 7.5 m e profondità costante h (vedi figura). Un corpo
di massa m = 100 g è appoggiato ad una molla di costante elastica k = 10 3 N/m compressa. Se
si lascia libera la molla essa imprime al corpo un impulso di modulo 1.4 Ns. Calcolare: a) la
compressione iniziale della molla; b) per quali valori dell’angolo di inclinazione del piano il corpo
oltrepassa la buca.
1
ESERCIZIO 5
Un corpo di massa m scivola lungo un piano lungo s e inclinato di un angolo α rispetto all’orizzontale.
Il corpo parte da fermo dalla cima e scivola lungo il piano, dove agisce una forza orizzontale di
modulo |F| = β costante. Alla fine del piano inclinato la forza smette di agire e, dopo aver percorso
un tratto orizzontale senza attrito, il corpo va a colpire una molla di costante elastica k. a) Verificare se F è conservativa e calcolarne eventualmente l’energia potenziale; b) trovare la velocità del
corpo alla fine del piano inclinato; c) trovare la compressione della molla.
ESERCIZIO 6
Un corpo di massa m è posto in cima a un piano inclinato di un angolo α, scabro con coefficiente
di attrito µ ad un’altezza h dal suolo. Alla base del piano il corpo si muove su un piano orizzontale
liscio dove incontra una molla di costante elastica k. Determinare: a) la velocità con cui il corpo
raggiunge la fine del piano inclinato; b) la compressione della molla al primo urto; c) l’inclinazione
α del piano affinché il corpo risalga fino a fermarsi ad un’altezza pari a metà di quella iniziale, supponendo µ = 1/3.
SOLUZIONI
ESERCIZIO 1
a) Le dimensioni di α si trovano considerando che F è una forza e quindi ha le dimensioni di una
massa per una lunghezza diviso per un tempo al quadrato ([MLT −2 ]). Questo è valido per tutte le
componenti di F. Ricordando che i versori sono per definizione adimensionali, avremo quindi che
2 = MLT −2
x)
−3αx
y) −3αz2 = MLT −2
[F] = MLT −2 ⇒
z) [−6αyz] = MLT −2
x) −3αx2 = MLT −2 ⇒ [α] x2 = MLT −2
⇒ [α] L2 = MLT −2 ⇒ [α] = ML−1 T −2
Si può facilmente verificare che il risultato soddisfa anche la y) e la z).
b) Si può facilmente verificare che U ha le dimensioni di un’energia:
[U ] = [α] x3 = ML−1 T −2 L3 = ML2 T −2 = [E]
c) Avendo già calcolato le dimensioni di α, possiamo determinare la sua unità di misura nel sistema
internazionale. Avremo quindi che:
α = 2.5 kg m−1 s−2 = 2.5 J/m3
In un campo di forze conservative il lavoro associato a un percorso si calcola come differenza di
potenziale tra il punto iniziale e quello finale, nel nostro caso rispettivamente A e B:
LAB = UA −UB = αx3 + 3αyz2 (1,2,−1) − αx3 + 3αyz2 (2,1,1) =
= α[(1 m3 ) + 3 ∗ (2 m) ∗ (1 m2 )] − α[(2 m)3 + 3 ∗ (1 m) ∗ (1 m2 )] =
2
α[(1 m3 ) + (6 m3 ) − (8 m3 ) − (3 m3 )] = (2.5 J/m3 ) ∗ (−4 m3 ) = −10 J
ESERCIZIO 2
In figura sono segnate in rosso le forze agenti sulla pallina appesa al filo una volta raggiunta la
nuova posizione di equilibrio data dal vento. Dato il sistema di riferimento considerato, avremo
che F = −F î = −kv2 î.
a) Per calcolare il lavoro compiuto da F lungo il percorso, possiamo usare il teorema delle forze
vive. Avremo quindi che il lavoro totale compiuto da tutte le forze in gioco sarà pari alla differenza
di energia cinetica ∆K:
1
1
Ltot = ∆K ⇒ LP + LT + LF = K f − Ki = mv2f − mv2i ⇒ LP + LT + LF = 0
2
2
dove si è tenuto conto che le velocità iniziale e finale sono nulle (la pallina è inizialmente in quiete
all’inizio e dopo l’azione del vento è nuovamente ferma).
La forza peso è una forza conservativa quindi il suo lavoro può essere calcolato come differenza di
energia potenziale:
LP = Ui −U f = mg ∗ 0 − mgh = 0 − mg(l − l cos ϕ) = mgl(cos ϕ − 1)
dove si è fissata la quota iniziale come corrispondente
a U = 0. Il lavoro della tensione si calcola
dalla definizione di lavoro come LT = T · ds. Poiché il corpo si sposta perpendicolarmente al
filo lungo cui è diretta la tensione si ha che T ⊥ ds in ogni punto, quindi L T = 0. Riscrivendo
l’equazione del teorema delle forze vive si ha che:
mgl(cos ϕ − 1) + 0 + LF = 0 ⇒ LF = mgl(1 − cos ϕ) = 2.45 J
b) Il sistema raggiunge l’equilibrio, quindi uno stato in cui sulla sferetta agiscono forze con risultante nullo (F + T + P = 0). Determinati da questa condizione i vettori T e F, dall’espressione
della forza del vento F potrò calcolare poi la velocità v a cui soffia il vento:
3
F + T + P = 0 ⇒
x) − F + T sin ϕ = 0
⇒
y) − mg + T cos ϕ = 0
x) T sin ϕ = F
mg
y) T = cos
ϕ = 9.8 N
Abbiamo quindi ottenuto la tensione della fune che ha modulo T = 9.8 N.
c) Dall’equazione x del sistema precedente abbiamo:
F = T sin ϕ =
mg sin ϕ
= mg tan ϕ.
cos ϕ
Considerando che il testo del problema dà F = kv2 , possiamo eguagliare le due espressioni per F:
v=
mg tan ϕ
=
k
kv2 = mg tan ϕ ⇒
√
(0.5 kg) ∗ (9.8 m/s2 ) ∗ 3 √
= 4.9 ∗ 1000 m2 s2 = 70 m/s
3 ∗ 10−3 kg/m
ESERCIZIO 3
In figura è mostrata la situazione iniziale (in alto) e il punto di massima compressione della molla
(in basso). Essendoci la forza d’attrito l’energia meccanica non si conserva. È possibile però
utilizzare il teorema delle forze vive che permette di calcolare il lavoro totale conoscendo l’energia
cinetica finale e iniziale del corpo:
1
1
1
1
Ltot = K f − Ki = mv2f − mv2i = 0 − mv20 = − mv20
2
2
2
2
4
Posso calcolare il lavoro anche a partire dalla sua definizione. Trascurando la forza peso e la
reazione vincolare del piano che agiscono perpendicolarmente allo spostamento, otteniamo:
Ltot = Lattr + Lel =
f
i
Fattr · ds +
f
i
Fel · ds =
D+l
0
Fattr dx +
D+l
D
Fel dx
dove si è tenuto conto che le forze hanno direzione orizzontale come il moto, che la forza di attrito
agisce su tutto il tratto di lunghezza D + l, mentre la forza elastica agisce solo nel tratto finale tra
D e D + l. La forza di attrito in questo caso è Fattr = −µmg î, dove il segno “–” indica il verso della
forza opposto a quello del moto. Per la forza elastica invece si ha Fel = −k∆x î dove ∆x = x − D
nel tratto interessato. Sostituendo otteniamo:
2
D+l
D+l
D+l
x
D+l
µmgdx −
k(x − D) dx = −µmg[x]0 − k
=
Ltot = −
− Dx
2
0
D
D
2
D
D2
1
l2
2
2
= −µmg(D + l) − k
+ Dl + − D − Dl −
+ D = −µmg(D + l) − kl 2
2
2
2
2
Unendo le due espressioni del lavoro si trova il coefficiente d’attrito cercato:
mv20 − kl 2
1
1
−µmg(D + l) − kl 2 = − mv20 ⇒ µ =
2
2
2mg(D + l)
ESERCIZIO 4
a) Per calcolare la compressione della molla consideriamo cosa succede fra i punti O ed A. Non
essendoci forze non conservative, si può utilizzare la conservazione dell’energia meccanica:
O
A
O
O
A
A
Emecc
= Emecc
⇒ Ecin
+ Σi E pot,i
= Ecin
+ Σi E pot,i
⇒
1 2
1
1
mvO + mghO + kD2 = mv2A + mghA
2
2
2
dove D è la compressione iniziale della molla. Si noti che h O = hA , quindi i due termini relativi
all’energia potenziale gravitazionale si semplificano. Inoltre la velocità iniziale dell’oggetto è
nulla: vO = 0. L’equazione si semplifica e otteniamo:
1 2 1 2
m
kD = mvA ⇒ D = vA
.
2
2
k
Per trovare D occorre solo determinare vA che possiamo trovare dal teorema dell’impulso:
J = ∆q ⇒ J = ∆qx = mvA − mvO .
Essendo il corpo inizialmente fermo (v O = 0) si ha che:
J
.
m
Quindi, sostituendo nell’equazione precedente, si ottiene:
J
J m
=√
D=
= 0.14 m
m k
mk
J = mvA ⇒ vA =
5
b) Il corpo arriva in B con una velocità vB diversa da quella posseduta in A e inclinata di un angolo β rispetto all’orizzontale; dal momento in cui il corpo giunge in B, il suo moto prosegue
eseguendo una parabola. Per trovare il modulo vB della velocità in B si può utilizzare la conservazione dell’energia meccanica fra A e B, oppure fra O e B. Scegliendo quest’ultima opzione:
O
B
0
0
B
B
Emecc
= Emecc
⇒ Ecin
+ Σi E pot,i
= Ecin
+ Σi E pot,i
⇒
1 2
1
1
mvO + mghO + kD2 = mv2B + mghB
2
2
2
Come già detto vO = 0, inoltre abbiamo fissato hO = 0 e hB = h. Infine possiamo sostituire il
risultato di D per ottenere:
J2
1 2
2 J2
J2
2
= mvB + mgh ⇒ vB =
− mgh ⇒ vB =
− 2gh.
2m 2
m 2m
m2
Una volta trovata la velocità in B, che esprimo come
vB = vB cos βî + vB sin β jˆ
fisso un SdR con origine nel punto in basso a sinistra della buca, come in figura, e scrivo le
equazioni orarie per le coordinate x (orizzontale) e y (verticale), che in questo caso descrivono
un moto parabolico:
x(t) = vBt cos β
y(t) = h + vBt sin β − 12 gt 2
dove si è fissato l’istante t = 0 come quello in cui il corpo si trova in B(0, h). Definiamo t C
come l’istante in cui x(tC ) = xC = L, cioè come l’istante in cui la coordinata x del punto materiale
raggiunge l’altro estremo della buca. Dalla prima delle equazioni precedenti avremo quindi che
x(tC ) = L ⇒ L = vB tC cos β ⇒ tC =
L
.
vB cos β
Sostituendo nell’altra equazione del sistema otteniamo il corrispondente valore della coordinata y:
2
1
L
L sin β 1 gL2
L
sin β − g
− 2
= h+
y(tC ) = h + vB
vB cos β
2
vB cos β
cos β
2 vB cos2 β
che dipende dall’angolo β. Affinché il corpo oltrepassi la buca dovremo avere:
y(tC ) ≥ yC = h.
Otteniamo quindi una disequazione con β come incognita:
h+
L sin β 1 gL2
≥ h.
− 2
cos β
2 vB cos2 β
Semplificando le h e moltiplicando per
2(vB cos β)2
L
2v2B sin β cos β − gL ≥ 0 ⇒ sin 2β ≥
si ottiene:
gL
⇒ sin 2β ≥
v2B
6
gL
J2
m2
− 2gh
⇒ sin 2β ≥
1
2
dove si è sostituito il risultato ottenuto in precedenza per v B . Risolvendo la disequazione otteniamo
infine i valori di β cercati:
arcsin
1
1
≤ 2β ≤ 180◦ − arcsin ⇒ 30◦ ≤ 2β ≤ 150◦ ⇒ 15◦ ≤ β ≤ 75◦
2
2
NB: questa parte dell’esercizio si sarebbe potuta anche risolvere utilizzando la definizione di gittata
(vedi la Cinematica).
ESERCIZIO 5
In figura è mostrato il sistema in esame: la zona colorata è quella di azione della forza F che, dato
il SdR, si esprime come F = β î, con il segno di β che ne determina il verso.
a) Per verificare se F è conservativa, ne calcolo il lavoro su un percorso generico e dimostro che è
indipendente dal percorso, e dipendente solo dai suoi estremi r 1 e r2 :
L1,2 =
r2
r1
F · dr = F ·
r2
r1
dr = F · (r2 − r1 ) = βx.
Si ha che F è conservativa (l’ultimo passaggio segue dal fatto che solo Fx = 0), e l’energia potenziale V corrispondente vale V (x, y, z) = −βx (avendo scelto VO = 0).
b) Per trovare la velocità alla fine del piano posso utilizzare la conservazione dell’energia meccanica tra il punto di partenza A(0, s sinα) e il punto B(s cos α, 0), perché tutte le forze agenti sul
corpo sono conservative:
A
B
A
B
Emecc
= Emecc
⇒ Ecin
+U A +V A = Ecin
+U B +V B
dove U è l’energia potenziale gravitazionale, che posso esprimere come U (x, y, z) = mgy (con
A = 0), l’equazione precedente
U (0, 0, 0) = 0). Tenendo conto che il corpo parte da fermo in A (Ecin
7
diventa:
1
0 + mgs sin α + 0 = mv2B + 0 − βs cos α ⇒ vB =
2
2s(mg sin α + β cos α)
m
c) Per calcolare la compressione della molla posso utilizzare la conservazione dell’energia meccanica tra B e il punto C di massima compressione della molla:
B
C
B
C
Emecc
= Emecc
⇒ Ecin
+U B +V B +W B = Ecin
+U C +V C +W C
(∗)
dove W indica l’energia potenziale elastica associata alla molla. Per x > s cos α la forza F è nulla
quindi il suo potenziale V non varia, rimanendo uguale al valore che assume in B. Infatti, preso un
punto generico di coordinata x0 > s cos α, avremo che
V (x0 ) = V B − LB→x0 = V B −
x0
s cos α
0dx = V B
In particolare si avrà quindi che V C = V B , quindi i due termini si elidono in (*). Inoltre, per come
è stata definita U , si ha U B = U C = 0. Posso definire l’energia potenziale elastica associata alla
molla come W = 12 kD2 , dove D è la compressione. L’equazione di conservazione dell’energia
meccanica (*) diventa quindi:
1
1 2
mvB + 0 = 0 + kDC2
2
2
C = 0. Risolvendo
dove DC è la compressione massima, e dove si è tenuto conto che vC = 0 ⇒ Ecin
l’equazione si ottiene:
m 2
2s(mg sinα + β cos α)
2
.
DC = vB ⇒ DC =
k
k
In alternativa, si può anche applicare la conservazione dell’energica meccanica tra A e C. Inserendo
solo i termini non nulli si ha:
1
A
C
= Emecc
⇒ mgs sin α = −βs cos α + kDC2
Emecc
2
che porta allo stesso risultato.
8
ESERCIZIO 6
a) L’attrito non è una forza conservativa quindi non posso utilizzare la conservazione dell’energia
meccanica. Posso però usare il teorema delle forze vive che lega il lavoro totale compiuto dalle
forze che agiscono sul corpo all’energia cinetica iniziale (punto A) e finale (punto B):
1
1
1
1
Ltot = K f − Ki = mv2B − mv2A = mv2B − 0 = mv2B
2
2
2
2
Poichè R è sempre perpendicolare allo spostamento, essa non compie lavoro. Si avrà quindi che
Ltot = LP + Lattr . La forza peso è conservativa quindi per trovare il lavoro compiuto posso usare la
differenza di energia potenziale U:
LP = Ui −U f = mghA − mghB = mgh − mg ∗ 0 = mgh
La forza di attrito, che agisce come indicato in figura, ha il modulo che dipende da R:
Fattr = µR = µP cos α = µmg cos α
Si avrà quindi che:
Lattr =
B
A
Fattr · ds =
B
A
(−µmg cos α)ds = −µmgs cos α
dove s è la lunghezza del piano. Poiché s = h/ sin α, si ha
Lattr = −µmgh cot α
(∗)
Sostituendo le espressioni trovate per i lavori nell’equazione del teorema delle forze vive si ha:
1
Ltot = LP + Lattr = mv2B ⇒
2
9
1
1
mgh − µmgh cotα = mv2B ⇒ v2B = (1 − µ cot α)gh ⇒ vB = 2(1 − µ cot α)gh
2
2
b) La massima compressione dC della molla si ottiene imponendo la conservazione dell’energia
meccanica tra B e C, dato che il piano orizzontale è privo di attrito per ipotesi. Quindi:
B
C
= Emecc
⇒ K B +U B +W B = KC +U C +W C
Emecc
dove abbiamo indicato con W l’energia potenziale elastica associata alla molla. Avendo B e C
la stessa quota sia ha che U B = U C , quindi i termini si eliminano. Inoltre, indicando con d la
compressione della molla, W = 1/2kd 2 quindi W B = 0 (la molla non è compressa) e W C = 1/2kdC2 .
Inoltre KC = 0 perchè il corpo si ferma quindi:
1 2
2(1 − µ cot α)mgh
(1 − µ cot α)mgh + 0 = 0 + kdC ⇒ dC =
2
k
c) Come nel caso a), sul piano inclinato è presente una forza dissipativa (l’attrito). Per calcolare
l’angolo d’inclinazione che porta il corpo a fermarsi a un’altezza h/2 devo utilizzare il teorema
delle forze vive tra il secondo passaggio in B e il punto D
Ltot = K D − K B = −K B
dove si è tenuto conto che K D = 0 perchè il corpo si ferma. Il lavoro totale sarà la somma del
lavoro della forza d’attrito e della forza peso: Ltot = Lattr + LP . Quindi il teorema delle forze vive
in questo caso ci dà la relazione
Lattr + LP = −K B
(♦)
È importante notare che nel percorso B → C → B l’energia si conserva, quindi al secondo passaggio
in B l’energia cinetica del corpo sarà ancora pari a
K B = (1 − µ cot α)mgh
Poiché abbiamo già calcolato la forza d’attrito e l’espressione corrispondente per il lavoro in (∗),
avremo che
1
Lattr = − µmgh cot α
2
Inoltre, come per il caso a), LP = U B − U D = −1/2mgh. Inserendo i termini trovati nella (♦)
ottengo:
1
1
− µmgh cot α − mgh = −(1 − µ cot α)mgh
2
2
dove α è l’unica incognita. Svolgendo i passaggi
µ cot α + 1 = 2(1 − µ cot α) ⇒ µ cot α + 2µ cot α = 2 − 1 ⇒
1
cot α =
⇒ tan α = 3µ ⇒ α = arctan(3µ)
3µ
Si noti come il risultato non dipenda da m, h e g, ma unicamente da µ. Sostituendo il valore µ = 1/3
indicato dal testo si ottiene
α = arctan(1) = 45◦
10