ESERCITAZIONE FISICA GENERALE 18/11/2013
Si risolvano gli esercizi esprimendo i risultati finali nelle unità del SI con due cifre
significative
Problema 1
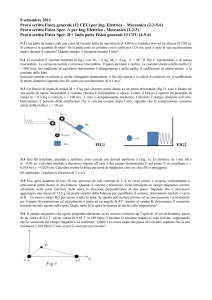
Un corpo scivola, partendo da fermo, dalla sommità del tetto di una casa, inclinato di un
angolo θ = 25o rispetto all’orizzontale (Fig. 1, sinistra). Il tetto presenta coefficiente di
attrito dinamico µ = 0.20. Il corpo si stacca dal tetto con una velocità in modulo pari a
v = 6.9 m/s; la base del tetto si trova a una quota h = 10 m rispetto a terra. Determinare
a) la lunghezza L del tetto;
b) la distanza d dalla casa alla quale il corpo tocca terra.
Problema 2
Una pallina di massa m = 1.5 kg viene lanciata orizzontalmente con velocità v0 = 3.2 m/s
contro un blocchetto di massa M = 2.0 kg inizialmente fermo su un piano orizzontale scabro
che presenta un coefficiente di attrito dinamico µd = 0.53. L’urto tra pallina e blocchetto è
totalmente anelastico. Il blocchetto è attaccato all’estremità di una molla il cui altro estremo
è fissato a una parete (Fig. 1, destra). In seguito all’urto, la molla subisce un accorciamento
massimo di ∆x = 13 cm. Determinare:
a) la velocità V del sistema pallina+blocchetto immediatamente dopo l’urto;
b) la costante elastica k della molla.
Figura 1: Illustrazioni relative all’esercizio 1 (sinistra) e 2 (destra).
ESERCITAZIONE FISICA GENERALE 18/11/2013
Soluzioni
Problema 1
a) Si può risolvere in due modi diversi. Un primo metodo consiste nello scrivere le forze e
quindi determinare l’accelerazione; una volta trovata l’accelerazione si può risalire alla
legge oraria e quindi allo spazio percorso. Un metodo alternativo consiste nell’utilizzare
il lavoro e l’energia. Dato che siamo in presenza di forze non conservative (c’è infatti
attrito), l’energia meccanica totale non si conserva: la sua variazione equivale al lavoro
fatto dalla forza d’attrito:
LN C = ∆Emecc
(1)
Il lavoro fatto dalla forza di attrito sull’intero percorso L vale
LN C = fatt L = −µd N L
(2)
dove N = m g cos θ è la componente normale della reazione vincolare e il segno meno
rende conto del fatto che la forza di attrito di oppone alla caduta. La variazione di energia
meccanica si può scrivere
1
∆Emecc = Kf + Uf − Ki − Ui = mv 2 + 0 − 0 − mgL sin θ
2
(3)
in cui si è posta l’energia potenziale gravitazionale uguale a 0 alla fine del tetto e si è
tenuto conto che la variazione di quota dall’inizio del tetto alla fine del tetto vale L sin θ.
Uguagliando LN C e ∆Emecc , si ricava dunque un’equazione nella sola incognita L:
1
−µd m g cos θL = mv 2 − mgL sin θ,
2
da cui
L=
1 2
v
2
g sin θ − µd g cos θ
= 10 m.
(4)
(5)
b) Una volta abbandonato il tetto, il corpo cade per effetto della gravità effettuando un moto
parabolico con velocità iniziale v che ha componente orizzontale v0x = v cos θ diretta
verso sinistra e componente verticale v0y = v sin θ diretta verso il basso. Le equazioni
parametriche del moto si possono scrivere:
x(t) = −v cos θt
1
y(t) = h − v sin θt − gt2
2
(6)
(7)
in cui si è posto che all’inizio del moto parabolico il corpo parte dal punto di coordinate
(0, h). Il corpo tocca terra nel punto di coordinate (−d, 0). Il tempo t∗ necessario perché
il corpo tocchi terra, ovvero la quota y diventi 0, si ricava da:
1
0 = h − v sin θt∗ − gt∗2 .
2
(8)
Si tratta di un’equazione di secondo grado nell’incognita t∗ . Si ricava:
s
v
sin
θ
v 2 sin2 θ 2h
t∗ = −
±
+
g
g2
g
(9)
ovvero t∗ = 1.2 s, scartando la soluzione negativa che non ha fisicamente senso. Infine, la
distanza d dalla casa a cui il corpo tocca terra si ricava da:
d = v cos θt∗ = 7.3 m.
(10)
Problema 2
a) Si tratta di un urto unidimensionale totalmente anelastico in cui il corpo di massa M è
inizialmente fermo. Dalla conservazione della quantità di moto tra l’istante subito prima
dell’urto e l’istante subito dopo l’urto ricaviamo:
mv0 + 0 = (m + M )V
da cui
V =
mv0
= 1.4 m/s.
m+M
(11)
(12)
b) Subito dopo l’urto, abbiamo un corpo di massa m+M che si muove per effetto della forza
elastica esercitata dalla molla, frenato dall’attrito. Conviene utilizzare ancora lavoro ed
energia. Il lavoro fatto dalla forza d’attrito su un percorso ∆x vale
LN C = fatt ∆x = −µd N ∆x
(13)
dove N = (m + M ) g è la componente normale della reazione vincolare e il segno meno
rende conto del fatto che la forza di attrito di oppone al moto. Il lavoro della forza
d’attrito equivale alla variazione di energia meccanica ∆Emecc ; si può scrivere
1
1
∆Emecc = Kf + Uf − Ki − Ui = 0 + k(∆x)2 − (m + M )V 2 − 0
2
2
(14)
in cui si è tenuto conto che l’energia cinetica finale vale 0 quando la molla è massimamente
compressa, l’energia potenziale finale ha il suo valore massimo 12 k(∆x)2 , l’energia cinetica
iniziale vale 21 (m + M )V 2 e l’energia potenziale iniziale vale 0, essendo la molla a riposo.
Uguagliando LN C e ∆Emecc abbiamo un’equazione nell’unica incognita k:
1
1
−µd (m + M )g∆x = k(∆x)2 − (m + M )V 2
2
2
da cui
k=
1
(m
2
+ M )V 2 − µd (m + M )g∆x
= 1.2 × 102 N/m.
1
2
(∆x)
2
(15)
(16)