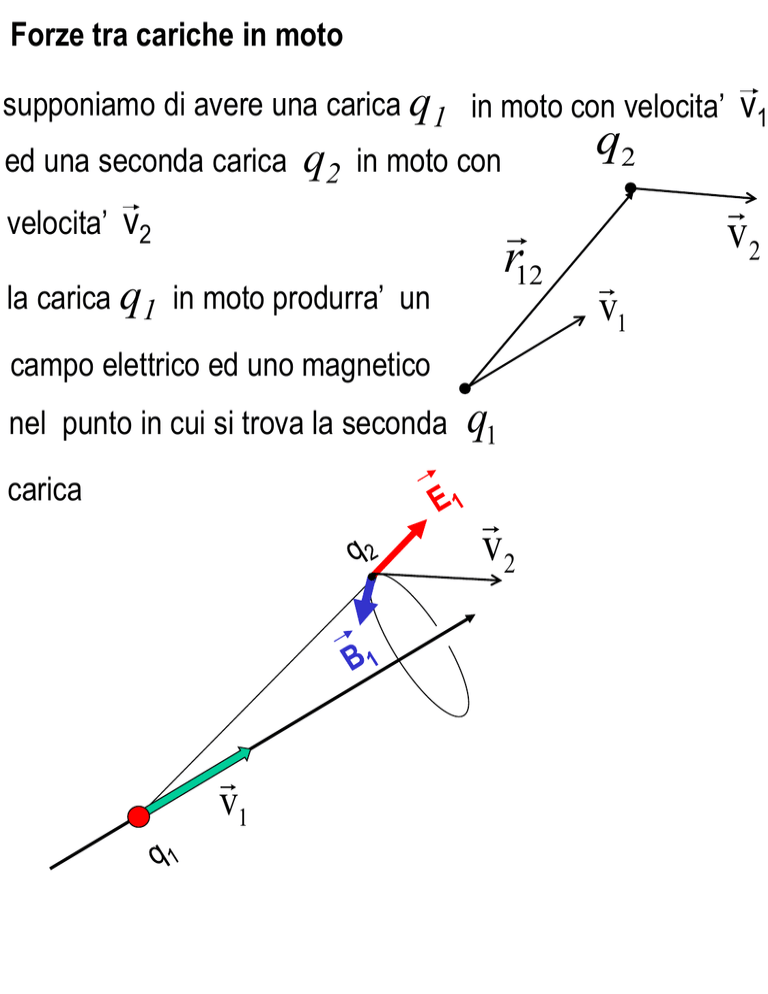
Forze tra cariche in moto
supponiamo di avere una carica q1 in moto con velocita’ v1
ed una seconda carica
q2
q2
in moto con
velocita’ v2
r12
la carica q1 in moto produrra’ un
campo elettrico ed uno magnetico
nel punto in cui si trova la seconda
carica
q1
v2
v1
v1
v2
supponendo che le velocita’ v1 e v2 siano
basse rispetto alla velocita’ della luce si ha
1 q1
E1 =
rˆ
2 12
4πε 0 r12
dove il vettore
r12
e =
B1 ε 0 µ0v1 × E1
parte dalla prima carica e punta verso
la seconda carica e dove si e’ posto r12 = r12 rˆ12
dunque la forza F12 che la carica q1 esercita sulla carica
q2 in moto con velocita v2
sara’
F12 = q2 E1 + q2 v2 × B1
operando in modo analogo a partire dalla seconda carica
si ottiene
F21 = q1E2 + q1v1 × B2
da notare che F12 ≠ F21
in generale : le forze tra le cariche in moto non sono uguali
ed opposte come richiesto dal principio di azione e reazione
ma occorrebbe tener conto della presenza di quantita’ di
moto “ in volo “ associata al campo elettromagnetico
per definizione la circuitazione del campo magnetico
calcolata lungo una linea chiusa γ e’
Γγ ( B ) =
⋅
B
dl
∫
γ
Teorema di Ampere
la circuitazione del campo magnetico calcolata lungo una
linea chiusa γ che concateni la corrente i e’ pari a
∫γ
B ⋅ dl =
µ0i
teorema di Ampere in
forma integrale
mentre la circuitazione e’ nulla se la corrente non e’
concatenata con il circuito
per semplicita’ consideriamo un piano perpendicolare al filo
e assumiamo come circuito chiuso γ una circonferenza
giacente su quel piano e concentrica con il filo
Orientiamo γ in base al senso di
i
percorrenza della corrente nel filo
usando la regola della mano destra
lˆ
r̂
γ
ds
B
Γγ ( B ) =
∫ B ⋅ ds
γ
=
ds ds(lˆ × rˆ)
µ0i
B
(lˆ × rˆ)
=
ma per la legge di Biot Savart
2π r
µ0i ˆ
ˆ × rˆ)
ˆ
(
B
)
(
l
r
)
ds
(
l
Γ=
×
⋅
γ
∫γ 2π r
P
µ 0i
µ0i
2π r = µ0i
Γγ ( B ) =
ds =
∫
2π r
2π r γ
in conclusione il teoremadi Ampere afferma che
Γγ ( B ) =
∫γ
B ⋅ ds = µ0i
il teorema di Ampere e’ l’equivalente per il campo
magnetico del teorema di Gauss per il campo elettrico
indica cio’ che genera il campo magnetico
le origini del campo magnetico ( “le sorgenti” detto in
senso generico) sono le correnti elettriche
sfruttando il teorema di Stokes si ottiene l’espressione
del teorema di Ampere in forma differenziale
∇ × B = µ0 J
Magnetismo nella materia
gli atomi hanno momenti magnetici orbitali.
se si inserisce un materiale all’interno di un campo
magnetico esterno di intensita’ B0
si verifica sperimentalmente che l’intensita’ del campo
magnetico B all’interno del materiale e’ pari a :
B
= B0 + χ m B0
χm
e’ detta suscettivita’ magnetica
vi sono tre categorie di materiali:
• sostanze diamagnetiche
hanno suscettivita’ magnetica negativa e molto piccola
dovuta ad un momento magnetico indotto con direzione
opposta al campo magnetico inducente
• sostanze paramagnetiche
hanno suscettivita’ magnetica positiva ma piccola.
Il comportamento e’ dovuto all’allineamento dei dipoli
elementari nella direzione del campo inducente
• sostanze ferromagnetiche
hanno suscettivita’ magnetica molto grande >> 1 ,
inoltre la risposta del ferromagnete dipende dallo stato di
magnetizzazione precedente,
fenomeno detto “isteresi magnetica” es. magneti permanenti
nell’approssimazione semiclassica dell’atomo di Bohr
gli elettroni nel loro moto orbitale intorno al nucleo
dell’atomo possono essere pensati come fossero
microscopici dipoli magnetici ( correnti amperiane)
se
m
e’ il momento di dipolo magnetico medio di
un atomo ( molecola ) e n e’ la densita’ volumetrica di atomi
o molecole del mezzo materiale
in perfetta analogia con la trattazione microscopica
dei dielettrici si introduce il vettore di magnetizzazione
M
definito come il momento di dipolo magnetico per unita’ di
volume di un mezzo materiale
M = nm
in questo modi si spiegano il diamagnetisco e il
paramagnetismo ma gli elettroni oltre ai momenti
magnetici orbitali hanno un momento magnetico intrinseco
lo spin
meccanica quantistica
Backup Slides
supponiamo di avere una carica q1 in moto con velocita’ v1
v1
ed una seconda carica q2 in moto con
velocita’ v2
supponiamo che le velocita’ siano
q1
basse rispetto alla velocita’ della luce
la carica q1 in moto produrra’ nel punto
r12
q2
in cui si trova la seconda
carica un campo elettrico ed uno magnetico
v2
1 q1
E1 =
rˆ e dato che
=
B ε 0 µ0 v × E
2 12
4πε 0 r12
µ0 v1 × rˆ12
B1 = q1
2
r12
4π
dove r12 e’ il vettore congiungente le cariche
ossia il vettore che parte dalla prima e punta verso
la seconda carica e dove si e’ posto
r12 = r12 rˆ12
con
r12 = r12
dunque la forza F12 che la carica q1 esercita sulla carica
q2 in moto con velocita v2 sara’
I1
I2
I3











