ALGEBRA LINEARE: LEZIONI DAL 22 NOVEMBRE AL 13 DICEMBRE
Sommario delle lezioni
• 22 Nov: Lezione 19. Esempi: matrici associate ad una applicazione lineare in varie basi.
Matrice di una simmetria ortogonale. (un’ora)
• 23 Nov: Lezione 20. Equazioni cartesiane in riferimenti diversi. Esempio: equazione di
una circonferenza in un riferimento non euclideo. (un’ora)
• 27 Nov: Lezione 21. Funzioni differenziabili e differenziali. Definizione di funzione derivabile da R a R. Generalizzazione a dimensione alta. Una funzione f : Rm → Rn è
differenziabile se esiste una migliore approssimazione lineare. La composizione di applicazioni differenziabili è differenziabile. Differenziale di funzioni composte. Differenziale di
funzioni da R a Rn : il vettore velocità. Differenziale di funzioni da Rn a R: il gradiente.
(due ore)
• 29 Nov: Lezione 22. Sviluppo di una funzione razionale in frazioni parziali. Unicità della
scomposizione attraverso l’algebra lineare. Teorema fondamentale dell’algebra, divisione tra
polinomi. Curve in R2 . Curve in R2 definite in forma implicita e parametrica. Esempio:
un’ellisse. Significato geometrico del vettore velocità e del gradiente. Il gradiente della
funzione che esprime una curva come sua curva di livello è sempre ortogonale alla curva.
(due ore)
• 4 Dic: Lezione 23. Il teorema del Dini in due dimensioni. Relazione tra un luogo di zeri
in R2 e una curva. Il concetto di curva regolare. Parametrizzazioni regolari di curve. Regolarità del luogo di zeri di una funzione φ : R2 → R quando ∇φ 6= 0. Lunghezza di archi di curva.
La distanza percorsa come integrale della velocità istantanea. La velocità istantanea è il
modulo del vettore velocità. Formula per il calcolo della lunghezza di un arco di curva.
Calcolo della lunghezza di un arco di circonferenza attraverso parametrizzazioni diverse.
(due ore)
• 6 Dic: Lezione 24. La parametrizzazione per lunghezza d’arco. Come passare da una parametrizzazione qualsiasi a quella per lunghezza d’arco. Esempi: parametrizzazione lineare
di una retta, e corrispondente parametrizzazione per lunghezza d’arco. Parametrizzazione di un moto circolare non uniforme, e relativa parametrizzazione per lunghezza d’arco.
Nella parametrizzazione per lunghezza d’arco le grandezze geometriche e le grandezze cinematiche sono ricavabili le une dalle altre. Coordinate polari. Definizione e formule di
cambiamento di coordinate tra coordinate cartesiane e coordinate polari. Equazioni di
rette e circonferenze in coordinate polari. (due ore)
• 7 Dic: Lezione 25. Il vettore accelerazione. Se la velocità istantanea è costante, avverto
una forza apparente ortogonale al moto. Accelerazione centripeta (centrifuga) in un moto
circolare uniforme. La curvatura. L’accelerazione centripeta come misura della curvatura di
un moto. Definizione di curvatura in un punto di una curva. Il triedro di Frenet. I vettori
tangente, normale e binormale. Derivate dei vettori del triedro di Frenet. La torsione.
(un’ora)
• 11 Dic: Lezione 26. Ripasso e domande. (due ore)
• 13 Dic: Lezione 27. Calcolo degli invarianti geometrici di una curva. Come calcolare curvatura e torsione senza passare per lunghezza d’arco. Scomposizione dell’accelerazione in
accelerazione tangenziale e accelerazione normale. La lunghezza della componente normale del vettore accelerazione è l’accelerazione istantanea. Il piano osculatore. Esempi di
parametrizzazione di curve e di calcolo degli invarianti geometrici. (due ore)
Risultati essenziali.
Funzioni differenziabili. In questi ultimi appunti tiro via un po’ velocemente su quello che
abbiamo fatto. Una funzione f : R → R si dice differenziabile in un punto x0 se esiste a ∈ R tale
che
f (x0 + h) = f (x) + ah + o(h).
1
2
ALGEBRA LINEARE I
Questa definizione è completamente equivalente a quella usuale data con il limite del rapporto
incrementale, che in questo caso vale semplicemente a. L’aspetto interessante della definizione
data nel nostro modo è l’immediata generalizzazione a dimensione alta.
Dico che l’applicazione F : Rm → Rn è differenziabile in un punto x0 ∈ Rm se esiste A : Rm →
Rn lineare tale che
F (x0 + h) = F (x0 ) + A(h) + o(|h|),
Rm .
dove h ∈
Sto in pratica chiedendo che F coincida con un’applicazione lineare a meno di
termini che vanno a zero più che linearmente. In questo caso A si dice differenziale della funzione
F nel punto x0 , e si indica con dF (x0 ). Ad esempio il differenziale di una funzione f : R → R è
l’applicazione lineare da R in sé data dal prodotto per la derivata di f in x0 .
Abbiamo fatto vedere a lezione che la composizione di funzioni differenziabili è differenziabile,
e che d(F ◦ G)(x0 ) = dF (G(x0 )) ◦ dG(x0 ), che è la generalizzazione a funzioni di più variabili della
derivata di funzioni composte.
Siccome i nostri differenziali sono applicazioni lineari, possiamo rappresentarli per mezzo di
matrici. In tal caso l’espressione appena scritta per il differenziale di funzioni composte ci dice
come ottenere il differenziale di una funzione composta come prodotto righe per colonne dei
differenziali delle due funzioni che vado a comporre.
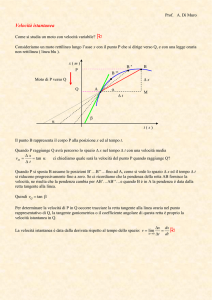
Curve in Rn . Una curva, o curva regolare, in Rn è un’applicazione γ : R → Rn di classe C 1 con
la proprietà che dγ non sia mai nullo. Abbiamo visto che per una funzione γ(t) = (x(t), y(t), z(t))
questo significa richiedere che il vettore velocità γ̇(t) = (ẋ(t), ẏ(t), ż(t)) non sia il vettore nullo per
alcun valore di t.
In altre parole, un’applicazione da R a Rn non è solo una curva, ma anche un modo di percorrerla, e noi stiamo chiedendo che la velocità istantanea esista in ogni punto di questa traiettoria,
e non sia mai nulla. Il vettore velocità è il vettore tangente alla nostra curva la cui lunghezza
sia pari alla velocità istantanea nel punto. La lunghezza dell’arco di curva compreso tra t = t0 e
t = t1 è pari a
Z t1
l=
|γ̇(t)|dt,
t0
ovvero all’integrale della velocità istantanea v(t) = |γ̇(t)|. Possiamo utilizzare la lunghezza percorsa per parametrizzare la nostra curva. Questo significa esprimere γ(t) non in funzione di t ma
in funzione di
Z t
s(t) =
|γ̇(x)|dx.
0
s si dice parametro di lunghezza d’arco, e la corrispondente parametrizzazione è la parametrizzazione per lunghezza d’arco.
Il teorema del Dini. Si dice teorema del Dini invece che più italianamente “teorema di Dini” solo
perché Ulisse Dini era pisano, e a Pisa mettono l’articolo davanti a qualsiasi nome di persona.
Detto questo, il teorema del Dini dice una cosa abbastanza intuitiva, e cioè che se prendo il luogo
di zeri di una funzione φ : R2 → R, in generale mi verrà fuori una curva. Però questo teorema
mi dice esattamente quando mi possa aspettare una cosa del genere, e cioè se φ è una funzione
di classe C 1 ed il suo gradiente nei punti in cui φ(x, y) = 0 non si annulla. In quel caso per il
luogo di zeri di φ riesco a dare una parametrizzazione regolare, e quindi il luogo di zeri è (almeno
localmente) una curva. Abbiamo anche dato esempi di questo, mostrando cosa può accadere se il
gradiente si annulla.
Invarianti geometrici di una curva. Se percorro una curva parametrizzata per lunghezza
d’arco (t = s), il vettore accelerazione γ̈(t) è rivolto verso l’interno della curva ed è ortogonale
alla curva che sto percorrendo. Nel caso in cui io stia percorrendo una circonferenza, so che il
modulo dell’accelerazione è uguale alla curvatura e cioè all’inverso del raggio della circonferenza
stessa. Allora ho definito la curvatura c in un punto di una curva come la lunghezza del vettore
accelerazione: c = |γ̈(s)|. Se utilizzo altre parametrizzazioni, in generale ottengo vettori accelerazione diversi, che non sono né della lunghezza giusta, né necessariamente ortogonali alla curva.
E’ quindi importante scegliere la parametrizzazione giusta per poter definire la curvatura.
Di solito si definisce una base ortonormale (cioè un sistema di riferimento euclideo) attorno
ad ogni punto di una curva in R3 , detto triedro di Frenet. Questo è composto di tre vettori
detti vettori tangente, normale e binormale. Il vettore tangente T è semplicemente il vettore
velocità normalizzato a lunghezza 1, o se vogliamo il vettore velocità che ottengo utilizzando la
parametrizzazione per lunghezza d’arco.
ALGEBRA LINEARE I
3
Il vettore normale N è il vettore di lunghezza 1 diretto nello stesso senso del vettore accelerazione che ottengo utilizzando la parametrizzazione per lunghezza d’arco. In altre parole
d
T (s) = c(s)N (s).
ds
Il vettore binormale si ottiene completando T ed N ad una base ortonormale di orientazione
positiva, cioè scegliendo B = T × N . Si mostra (e lo faccio vedere nell’ultima lezione) che
d
ds T (s) = c(s)N (s)
d
N (s) = −c(s)T (s) − τ (s)B(s)
ds
d
B(s) = τ (s)N (s)
ds
dove τ è un altro invariante geometrico detto torsione della curva nel punto. Se la mia curva giace
in un piano, allora la torsione è nulla. La torsione misura di quanto la curva stia uscendo dal piano
che meglio la contiene, detto piano osculatore della curva. Il piano osculatore sarà ovviamente il
piano che contiene il punto della curva che sto considerando, la velocità in quel punto, ed anche
l’accelerazione in quel punto. A lezione faccio l’esempio di un’elica che non è contenuta in nessun
piano, e si torce sempre nella stessa misura (la torsione è costante). Con il teorema di esistenza
ed unicità per soluzioni di equazioni differenziali, che non avete ancora fatto in analisi, potrete
mostrare che una curva in R3 di curvatura e torsione date è unica, a meno di traslazioni e rotazioni.
Per terminare, un po’ di conti con i vettori del triedro di Frenet. Supponiamo di non stare
utilizzando la parametrizzazione per lunghezza d’arco. Allora:
d
ds
d
X(t) =
X(s) ·
,
dt
ds
dt
e sappiamo che ds/dt è la velocità istantanea v(t). Allora abbiamo: γ̇(t) = dγ(s)/ds · v(t) = v(t)T ,
cioè qualcosa che già sappiamo. Il vettore velocità è tangente alla mia curva e la sua lunghezza è
la velocità istantanea. Andiamo a derivare γ̇(t) per ottenere:
d
(v(t)T ) = a(t)T + v(t) · T = a(t)T + v 2 (t)c(t)N,
dt
dove a(t) è la derivata della velocità istantanea, e cioè l’accelerazione istantanea. Questo vuol
dire che il vettore accelerazione ha una componente tangenziale ed una normale, e che il modulo
di quella tangenziale è pari all’accelerazione istantanea, mentre quello di quella normale (l’accelerazione centripeta) è pari al quadrato della velocità istantanea moltiplicato per la curvatura. Il
...
calcolo di γ (t) è un po’ più noioso, e porta a:
...
γ (t) = (a0 − v 3 c2 )T + (3vac + v 2 c0 )N − v 3 cτ B.
...
e non è particolarmente illuminante, a meno che non si noti che γ̇ × γ̈ = v 3 cB e che (γ̇ × γ̈) · γ =
6
2
−v c τ . Ricordando che |γ̇| = v, avremo:
...
|γ̇ × γ̈|
(γ̇ × γ̈) · γ
c=
,
τ
=
−
,
|γ̇|3
|γ̇ × γ̈|2
γ̈(t) =
che esprimono curvatura e torsione come funzioni di grandezze cinematiche rispetto ad una
parametrizzazione qualsiasi.
Dipartimento di Matematica, Università degli studi di Roma – “La Sapienza”
E-mail address: [email protected]