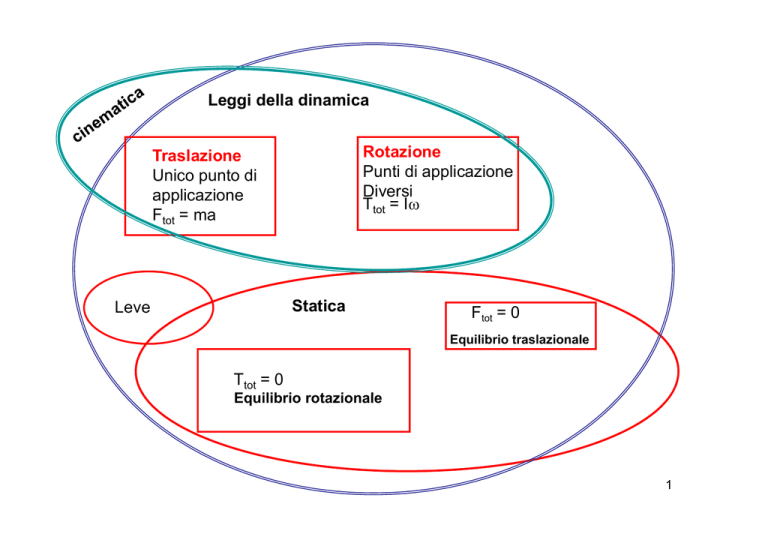
Leggi della dinamica
Rotazione
R
t i
Punti di applicazione
Diversi
Ttot = Iω
Traslazione
Unico punto di
applicazione
Ftot = ma
Statica
Leve
Ftot = 0
Equilibrio traslazionale
Ttot = 0
E ilib i rotazionale
Equilibrio
t i
l
1
La conservazione dell’energia
dell energia
•Il lavoro delle forze
•L’energia
L energia cinetica
•L’energia potenziale per forze “conservative”
•La conservazione dell’energia totale in assenza di attriti
•La conservazione dell’energia in presenza di attriti: il calore.
2
Il lavoro di una forza
Fm
0
Peso
La forza peso comprime la molla che si
deforma di x cm
cm.
La forza con cui la molla si oppone alla compressione
È pari a
Fm = - K x
x
Attenzione: la deformazione cresce
nel tempo
La compressione
p
smette q
quando si
giunge all’equilibrio fra
Fm e il Peso: Fm + Peso = 0
Kx = Peso
x = Peso/K
La forza
f
peso e la forza
f
elastica della molla hanno compiuto un lavoro?
?
3
Lavoro: forza e spostamento
Tutte le volte che la forza applicata induce uno spostamento
diciamo che la forza ha compiuto un lavoro sul sistema a cui è applicata
Perché questa definizione?
Lavoro Æ effetto
spostamento
deformazione
4
v
Il lavoro di una forza
Fm
Fm
Peso
Che si
trasforma
in un corpo
i movimento
in
i
Peso
Il sistema in seguito alla deformazione
d ll molla
della
ll acquisisce
i i
una ““capacità”
ità” ((chiamiamola
hi i
l energia)
i )
Può compiere a sua volta un lavoro
mettendo
tt d in
i moto
t un corpo
5
Quindi:
•Compressione della molla: deformazione della molla
•Il sistema si ferma all’equilibrio fra peso e forza elastica
•Il sistema ha acquisito la capacità
à di compiere altro lavoro:
abbiamo
bbi
““caricato”
i t ” lla molla
ll
abbiamo fornito energia alla molla
Ma il peso che aveva capacità di fare lavoro sulla molla all’inizio (molla estesa)
perde questa capacità quando scende comprimendo la molla.
Quindi: perchè la forza F compia lavoro, è essenziale che ci sia uno spostamento
del punto di applicazione della forza.
6
La forza peso durante la compressione lenta
Eguaglia la forza della molla che cresce:
L
Lavoro
=P*S
Spostamento
t
t
0
S
P
x
Lavoro = P * Spostamento
Per la scelta
del sistema
di coordinate
Joule (J) è l’unità di misura del lavoro
Corrisponde al lavoro fatto da una forza di 1 N
che induce uno spostamento di 1 m
Consideriamo SOLO la componente della forza parallela allo spostamento:
Perché?
7
F
Tutta l’ampiezza della forza
Va in moto del carrello
Tutta l’ampiezza della forza
Viene bilanciata dalla reazione dei binari
F
Solo la componente parallela della forza
Induce moto
F||
F
F⊥
l’ampiezza della forza perpendicolare al moto
Viene bilanciata dalla reazione dei binari
8
Il lavoro compiuto da una forza è dato dal prodotto
scalare della forza per lo spostamento.
L = F ⋅ s = Fs cos(θ )
F
θ
s
L>0
Lavoro
motore
θ
F
s
L=0
F
θ
s
L<0
Lavoro
resistente
9
Lavoro = F * Spostamento
Prodotto scalare
La forza peso durante la compressione lenta
eguaglia la forza della molla che cresce:
0
S
F
Lavoro = P * Spostamento = P x
P = kkx
x
Per la scelta
del sistema
di coordinate
L = kx2
Esempio: P = 100 N; x = 10 cm
Lavoro = 100 N x 0.1 m= 10 Nm = 10 J
In realta’ si può calcolare
più esattamente che
L = kx2/2
10
Approfondimento
facoltativo
Ruolo della dissipazione
Se il peso passa da 0 a P, abbiamo una deformazione rapida della molla:
Questo implica la presenza di dissipazione in termini di calore dissipato dalla molla
Se non voglio avere dissipazione devo fare cambiamenti che implichino
Velocità molto basse
basse.
Posso farlo pensando che istante per istante il peso aumenti in modo
da essere sempre bilanciato con la forza elastica della molla, che nel
processo di compressione cresce:
P(x) = - kx
Istante per istante
Allora il lavoro fatto dal peso sarà kx2/2
Esattamente uguale e contrario a quello fatto sulla molla.
11
Approfondimento
facoltativo
La forza elastica non è costante durante la compressione:
F = - kx
Felastica
0
(è diretta in verso
contrario allo spostamento)
Lavoro = F x Spostamento
S = deformazione
Come facciamo a calcolare il lavoro?
x
Possiamo generalizzare la definizione:
L
Lavoro
= F1S1 + F2 S2 + F3 S3 + ……
12
Approfondimento
facoltativo
Possiamo generalizzare la definizione:
Risultato generale:
Lavoro = F1S1 + F2 S2 + F3 S3 + ……
F
F
S1 S2
x1
F1=-kx1
Lavoro =
L
Area del grafico
Forza - spostamento
x
x2
x
x
F2=-kx2
F=-kx
kx 2
Lavoromolla = −
2
Compressione !!!
13
Il lavoro di compressione
p
della molla è calcolabile e risulta in realtà
Pari alla metà di quanto calcolato in base al peso che comprime la molla:
kx 2
Lavoromolla = −
2
Compressione !!!
Lavoro negativo : compressione
E in generale tutte le volte in
cui gli spostamenti sono
in verso opposto
alle forze (molla)
Chi ha compiuto questo lavoro per deformare la molla?
La forza PESO !!
QuindiÆ
LPeso = kx2/2
14
La molla viene deformata a discapito del lavoro della forza peso.
Il lavoro fatto sulla molla è disponibile per:
generare moto (velocità) o ulteriore deformazione.
Quale legame c
c’è
è fra il lavoro e la velocità impartita??
N.B.
F=ma
È una relazione fra la forza impartita e l’accelerazione
15
Esempio: supponiamo di spingere su un piano orizzontale un oggetto con
una forza F diretta lungo il piano.
piano
a 2
Spazio percorso = s = t
2
Velocità = v = at
v
t=
a
F
a v2 v2
s=
=
2
2a
2a
v2
v2
Lavoro = F * s = ma * s = ma *
=m
2
2a
16
Energia cinetica
Questo appena visto è un risultato generale:
Lavoro fatto dalle forze = variazione dell’energia cinetica
v
K =m
2
L = Kfin - Kin
Stato
finale
2
Unità di K:
Kg*
g m2/s2 = (Kg
g * m/s2)*m = N*m = J
Stato
iniziale
17
esempio
K = 10 N/m
/
Felastica = −kx
Felastica
x
•Serve 1 N per deformare la molla di 10 cm
•100 g di massa deformano la molla di 10 cm
•Se
Se una persona di 70kg salisse sulla molla la deformerebbe
di x = P/k = 700/10 m = 70m
Felastica
P
x
18
esempio
Se deformiamo la molla di 10 cm
il lavoro fatto contro molla è
x2
[ N ] 0.12 [m]2
L = −k
= −10
2
2
[ m]
= -5 ⋅ 0.01[N][m]
[ ][ ] = -0.05[J]
[]
Ora la molla è in grado di compiere un lavoro uguale e contrario
espandendosi
La molla è dotata di una energia potenziale elastica
Q
Questa
t è stata
t t acquisita
i it a discapito
di
it del
d l corpo che
h l’ha
l’h compressa
19
Legame fra Energia cinetica e lavoro meccanico
2
v
K =m
2
v2
v2
L = K fin − K in = m − 0 = m
2
2
Il lavoro fatto dalla molla in espansione
p
è “quasi”
q
uguale
g
e contrario a quello subito in compressione
x2
v2
0.05[ J ] = k
=m
2
2
x2
L=k
2
x è la deformazione
parte molla espandendosi
p
da cui p
20
Legame fra Energia cinetica e lavoro meccanico
2
2
x
v
k
=m
2
2
Un corpo di massa 100g viene messo dalla molla in moto con v tale che:
mv2/2 = 0.05 J
v = 0.05 * 2 / m = 0.05 * 2 / 0.1 = 1m / s
21
Energia cinetica
Il corpo “sparato” dalla molla “caricata di energia” urta contro un materiale e
lo deforma o mette in moto un secondo corpo.
Lavoro in espansione
x2
k
2
Lavoro delle forze = Kfin - Kin
K all’inizio del movimento
K alla fine del movimento
x2
v2
k
= K fin − 0 = m
2
2
22
Energia cinetica
Reciprocamente un corpo che si ferma contro una molla mentre
si muove a una velocità V Æ deforma la molla
Lavoro in compressione
x2
−k
2
Lavoro delle forze = Kfin - Kin
K all’inizio
all’ini io del mo
movimento:
imento:
È uguale a zero
K alla fine del mo
movimento:
imento:
È diversa a zero
x2
v2
−k
= 0 − K in = − m
2
2
23
Esempio: piano inclinato
Assenza di attrito
P|| = (h/S) mg
h molto piccolo
P||
S
h
D
z
Il cubo scivola: il suo peso compie il lavoro
P|| S
Lavoro gravitazionale (discesa!) = mgh
=
h
mgS
g = mgh
g
S
24
Assenza di attrito
h molto
lt piccolo
i
l
h
L = mgS = mgh
S
P||
S
h
D
z
Il cubo parte da fermo
Kin = 0
Kfin = L
mv2/2 = mgh
v2 = 2gh
25
Assenza di attrito
h molto
lt piccolo
i
l
D≅S
h
L = mgS = mgh
S
P||
S
h
D
z
h = 10 cm
v = 2 gh = 20 * 0.1 = 1.4m / s
Indipendente dalla massa!!
26
Il segno del lavoro
LF = Fs > 0
LPeso = −mgh < 0
S
h
Fext
P||
D
Se il moto è molto lento….non c’è attrito (o molto poco) e
LF = - Lpeso
Il corpo sale contro la forza peso a discapito di qualche altro lavoro (muscolare)
27
Il segno del lavoro
LF = Fs > 0
LPeso = −mgh < 0
S
h
Fext
P||
D
Se il moto non è lento…. c’è attrito e la forza di attrito compie lavoro
Lf = -Ff * S sempre negativo
LF = - Lpeso - Lf = - Lpeso + |Lf|
Il corpo sale
l contro
t la
l forza
f
peso e l’attrito
l’ tt it a discapito
di
it di
qualche altro lavoro (muscolare) e generando calore sul piano
28
Energia cinetica,
cinetica lavoro e attrito
K = mv2/2
Lavoro fforze di attrito
L
tt it
Sempre negativo
L + Lf = Kfin - Kin
Stato
finale
Stato
iniziale
Kfin = Kin+L+Lf < Kin+L
Le forze di attrito limitano la conversione di lavoro meccanico in energia cinetica
cinetica.
29
Energia
g p
potenziale
UN ESEMPIO: la forza gravitazionale
L = mgh
0
xin
h
L = mg (xfin – xin) = mgxfin – mgxin = -Ufin + Uin= -(Ufin-Uin) = - ∆U
P
xfin
x
∆U = mgh
è detta variazione di energia
potenziale gravitazionale
Quella forma di energia che un corpo ha per il fatto si essere in una
determinata posizione (raggiunta con un certo spostamento….)
Forze per cui L = - ∆U sono dette forze conservative
30
Scelta di convenienza
convenienza…
Scegliamo di suddividere le forze che possono agire su un sistema in:
1. Forze gravitazionali
2 Forze
2.
F
di attrito
i
3. Tutte le altre forze che agiscono sul sistema
Il lavoro
l
fatto
f tt da
d TUTTE le
l forze
f
serve a modificare
difi
l’l’energia
i cinetica
i ti d
dell sistema
i t
31
Forze di attrito
Lg = - ∆Ug = mg(xfin-xin)
Altre forze applicate
Lavoro delle forze = Lg + Lf + LA = Kfin – Kin
Lavoro delle forze = Lg - |Lf| + LA = Kfin – Kin
Forze conservative sono quelle per cui il lavoro fatto NON dipende dal percorso
x0
In teoria…..
teoria
Non si compie lavoro:
h
x1
Si guadagna lavoro nella prima meta’ del
Percorso (L>0) e si compie lavoro nella
seconda metà (L<0) …
x
32
In realtà l’attrito c’e’ sempre!!!
Cabina di massa m
Il lavoro fatto dalle forze gravitazionali
è mgh nel tragitto in discesa
Mentre è –mgh nel tragitto in salita, ma !!!!
h
Le forze di attrito del p
perno della ruota
Agiscono sempre in modo da fare un lavoro
Negativo:
ovvero le forze di attrito sono sempre opposte
al movimento.
Lavoro delle forze = Lg + La = Kfin – Kin
Lg - |La|= Kfin – Kin
• A ogni giro il lavoro totale della gravitazione
è nullo: Lg = 0
• Lf <0
• ∆K = Kfin – Kin = -|Lf|<0
33
Analizziamo mezzo giro:
Cabina di massa m, v=vi
Il lavoro fatto dalle forze gravitazionali
è mgh nel tragitto in discesa
Mentre le forze di attrito fanno lavoro negativo
h
Lavoro delle forze = mgh - |La| = Kfin – Kin
Kfin = Kin + mgh - |La|
Modulo di L=|L| è
Il valore
l
con segno positivo
iti
vfin
Se l’attrito è piccolo, mgh – |La| > 0
Kfin > Kin
vfin > vin
34
Analizziamo mezzo giro, con attrito grande:
Cabina di massa m, v=vi
Lavoro delle forze = mgh - |La| = Kfin – Kin
Paragonabile a mgh
h
SE mgh
S
g - ||La| = 0.1
0 mgh:
g
v fin = vin2 + 2 gh / 10
C attrito
Con
tt it
v fin = vin2 + 2 gh
S
Senza
attrito
tt it
E in salita????
Lavoro delle forze = - mgh - |La| = Kfin – Kin
Non arriva in cima!!!!
35
Lavoro delle forze = Lg + Lf + LA = Kfin – Kin
Se non c’e’
c e attrito e non ci sono altre forze oltre alla gravitazione………….
gravitazione
Lg = mg (xfin – xin) = -Ufin + Uin
L = mgh
0
Uin – Ufin = Kfin – Kin
Uin + Kin = Ufin + Kfin
xin
Emec = U + K = costante
xfin
x
36
Energia meccanica in presenza di attrito?
Lavoro delle forze = Lg - |Lf| = Kfin – Kin
Lg = mg (xfin – xin) = -Ufin + Uin
L = mgh
Uin – Ufin - |Lf| = Kfin – Kin
Uin + Kin = |Lf| + Ufin + Kfin
0
xin
∆Emec = U + K = -|L
| f|
xfin
x
L’energia meccanica decresce per
Effetto dell’attrito
37
Esempio con il pendolo
t = 0s
0
v = v0 = 0
x = x0
x0
U0 = mgx0
x
v02
K0 = m = 0
2
Emec = U0 +0 = U0
38
Esempio con il pendolo
t = T/4
0
v = v1 > 0
x = x1 < x0
x0
h
v1
x1
x
Un quarto di periodo
U1 = mgx1
v12
K1 = m
2
Emec = U1 +K1 = U0
Da cui:
v12
m = mgh
2
v1 = 2 gh
Valore iniziale di Emec
39
Esempio con il pendolo
t = T/2
0
v = v2 = 0
x = x2= x0
x2
M
Mezzo
periodo
i d
U2 = mgx2 = U0
8
U
U0
energia [J]
x
v22
K2 = m = 0
2
U1
6
Emec = U2 = U0
4
2
0
K
S
Senza
attrito
0
200
400
tempo (s)
600
40
Esempio con il pendolo
0
0
x2
U2 = mgx
g 2 = U0
x1
x
x
U0
7
U1
energia
a [J]
6
5
4
Lf = ∆Emec = ∆U + ∆K <0
3
2
1
0
C attrito
Con
tt it
0
200
400
tempo (s)
600
41
∆U g = −mgH = −∆K = − K fin
fi
m 2
v fin = mgH
H
2
v fin = 2 ggH ≅ 44m / s ≅ 130km / h
H=100m
S
42
Frenata, in quanto spazio?
Attrito dinamico
v fin = 44m / s
µ d = 0.4
L f = −mgµ d S
Questo deve “mangiarsi”
Tutta l’energia
g cinetica
H
L f = − mgµ d S = ∆K
v 2fin
∆K = K fin − K in = 0 − m
L f = −mgµ d S = −m
v
2
2
fin
2
S=
v 2fin
2 gµ d
≅ 246m
S
43
Lavoro e calore
LF = Fs > 0
LPeso = −mgh < 0
LA = − µ D mgS < 0
h
S
Fext
D
P||
FA=µDP⊥S
La forza di attrito compie lavoro negativo
Kin = Kfin =0
0
LF = ∆Ug - LA+∆K = ∆Ug – LA = ∆Ug + Q
Calore(>0) fornito al cubo
44
Lavoro e calore
LF = Fs > 0
F = forza
muscolare
LPeso = −mgh < 0
LA = − µ D mgS < 0
h
S
Fext
P||
FA=µDP⊥S
D
•attrito sul piano (LA),
•lavoro (chimico-elettrico) nel nostro muscolo,
muscolo LF
•e “attrito interno” nel muscolo, Lm < 0
La + Lmuscolo + Lm + LF = ∆Ug
Q LA-L
Q=-L
Lm>0
0
Lmuscolo + LF = ∆Ug +Q
45
Lavoro muscolare
∆Uk = kx2/2
F = forza muscolare
0
S
Lm + LF = ∆Uk + ∆K
x
LF = lavoro muscolare (elettrico, chimico)
Lm = lavoro contro le forze di attrito interno del muscolo < 0
LF = ∆Uk + ∆K –Lm = ∆Uk + ∆K + Q
N.B. se F = mg, allora LF=-mgx
-2mgx+kx2 + Q=0
x = 2mg/k-Q
2 /k Q
46
gravitazionali
Forze
A
T
T
R
I
T
O
elastiche
S
P
O
altre…. Elettromagnetiche,
g
, nucleari,, etc..
S
T
A
M
E
Il LAVORO induce una
Lavoro = Forza * Spostamento
VARIAZIONE di ENERGIA N
T
O
Cinetica
ENERGIA
Potenziale: gravitazionale, elastica, etc…
CALORE
47
Leggi della dinamica
Traslazione
Unico punto di
applicazione
Ftot = ma
Rotazione
Punti di applicazione
Diversi
Ttot = Iω
Leggi di conservazione
Conservazione
dell’energia
Conservazione della
Quantità di moto
p = mv
48
Leggi di conservazione
in Fisica
Ftot = ma
Ftot = m
(v2 − v1 )
(t2 − t1 )
equilibrio
Ftot =
Ftot = 0
F
(mv2 − mv1 )
(t2 − t1 )
-F
49
Leggi di conservazione
in Fisica
(mv2 − mv1 )
Ftot =
=0
(t2 − t1 )
Se un corpo non è soggetto a forze
(o le forze si equilibrano) : Ftot =0
( mv2 − mv1 )
=0
(t2 − t1 )
mv2 − mv1 = 0
mv è detta quantità di moto
È un vettore !!!! Perché la velocità è un vettore
mv2 = mv1
50
Conservazione della
quantità di moto
Quantità di moto = p = mv
m
v
p=mv
p
p = m V = costante
51
Conservazione della
quantità di moto per
un sistema di corpi
3
1
v
2
Quantità di moto totale = p1 + p2 +….
+
Per un SISTEMA di CORPI non soggetto a forze
ESTERNE o per cui le forze si equilibrano:
La quantità di moto totale è costante
m1
v1
v2
m2
P = m1 V1 + m2 V2
v1
m1
m2
v2
È costante
PRIMA
DOPO
52
Un caso particolare: i corpi si deformano attaccandosi (urto anelstico)
p
Ptotdopo
= (m2 + m1 )v2
Ptotpprima = m1v1
Ptotprima = Ptotdopo
m2
m1
m1v1 = (m2 + m1 )v2
m1
v2 =
v1
(m2 + m1 )
53
Questo è vero anche se alcune forze INTERNE AL SISTEMA agiscono:
1. La forza peso degli oggetti che è bilanciata esattamente dal piano.
2. Le forze legate al contatto dei corpi, ovvero al vero e proprio urto.
Trascuriamo invece, nell’esempio, l’attrito.
Sistema di due corpi che urtano
54
Ftot = 0
1
v2
v1
2
F12 = -F
F21
F21
1
Ftot = F12 + F21 = 0
2 F12
Ftot = 0
v1
1
2
v2
55
Anche se ci sono forze INTERNE al sistema di corpi
la quantità di moto totale del sistema rimane invariata
invariata.
F12 = -F21
Infatti
att
In ogni istante
Ftot = 0
Sistema di due corpi che urtano
56
Esempio sulla conservazione della quantità di moto.
m v1 = m v2
v1 = v2
v1 > 0
v1=0
v2=0
v1 = 0
v2 = 0
v1 = 0
v2 > 0
v2 = 0
57
Esempio sulla conservazione della quantità di moto.
m1 v1 = m2 v2
v2 = m1v1/m2
m1
<<
m2
Al crescere della massa m2, la sfera pesante tende a rimanere ferma.
58
Esempio sulla conservazione della quantità di moto.
m1 v1 = m2 v2
v2 = m1v1/m2
m1
<<
m2
Al crescere della massa m2, la sfera pesante tende a rimanere ferma.
59
Esempio sulla conservazione della quantità di moto.
Il cannone spara mentre e’ sul vagone: applica una forza sul proiettile e subisce
una forza (il “rinculo”) uguale e contraria che trasmette al vagone
che va nel verso opposto al proiettile
Fcannone
Fproiettile
Fvagone
Il vagone dopo il colpo si muove di moto rettilineo uniforme in direzione
Opposta al colpo sparato.
60
Esempio sulla conservazione della quantità di moto.
Il cannone spara mentre e’ sul vagone: applica una forza sul proiettile e subisce
una forza (il “rinculo”) uguale e contraria che trasmette al vagone
che va nel verso opposto al proiettile
Il vagone dopo il colpo si muove di moto rettilineo uniforme in direzione
Opposta al colpo sparato.
61
Esempio sulla conservazione della quantità di moto.
Il cannone spara mentre e’ sul vagone: applica una forza sul proiettile e subisce
una forza (il “rinculo”) uguale e contraria che trasmette al vagone
che va nel verso opposto al proiettile
Ma vi è stato uno
p
netto
Spostamento
Del centro di massa di
Tutto il sistema
Quando il proiettile colpisce la parete del vagone e ci si conficca applica una
Forza al vagone che lo fa fermare: in questo modo la quantità di moto
Non è variata, ovvero rimane NULLA.
62
Esempio: quantità di moto
(ppalla + pmuro )prima = (ppalla + pmuro )dopo
p = m V = costante
ppi + pmi = ppo + pmo
pmi = 0 inizialmente il muro è fermo
Muro: Massa
molto grande
ppi=mvi
pmuro
ppi = ppo + pmo
ppo=mvo
63
Esempio: quantità di moto
ppi = ppo + pmo
Visto dall’alto
x
pix
pox
piy
poy
y
ppi,x = ppo,x + pmo,x
piy = -poy
ppi,y = ppo,y + pmo,y
64












