1.1.1.1
Algoritmo di Mallat
Partendo dalla famiglia di wavelet discrete diadiche e dal loro comportamento in frequenza al variare
dell’indice di scala j, Mallat suggerisce di decomporre un segnale utilizzando due famiglie di funzioni
wavelet: una famiglia di funzioni h j , k (t ) = 2 j / 2 h(2 j t − k ) con andamento in frequenza di tipo passa basso al
fine di estrarre dal segnale il contenuto in bassa frequenza (detto anche approssimazione), ed una famiglia
di funzioni g j , k (t ) = 2 j / 2 g (2 j t − k ) con andamento passa alto per estrarre il contenuto alle alte frequenze
del segnale (detto anche dettaglio). L’indice k determina la posizione temporale della funzione rispetto al
segnale.
La suddetta coppia di filtri è nota con il nome di ‘quadrature mirror filters’, perchè riguarda filtri che
godono della seguente proprietà :
n
g [ L − 1 − n ] = ( −1) ⋅ h[ n ]
dove L è il numero di campioni. In Fig. 13 è mostrato un esempio di segnale tipo ‘h’ e ‘g’.
Partendo dal valore j = 1, l’algoritmo di Mallat decompone il segnale in due sottobande uguali, ciascuna
pari a metà dello spettro del segnale da decomporre. Le ulteriori suddivisioni del segnale in sottobande si
possono ottenere mantenendo fissi i due filtri g[n] e h[n] ed effettuando una compressione, o decimazione,
del segnale all’uscita degli stessi, producendo un’espansione della banda del segnale.
Ricordiamo che un decimatore a M punti mantiene un solo campione ogni M e quindi il segnale decimato
è una versione contratta dello stesso, mentre lo spettro del segnale decimato risulta espanso di un fattore M
rispetto alla versione non decimata, e l'ampiezza viene ridotta di un fattore 1/M .
Im
h(n)
⏐H(ω⏐
x
a
x
Re
-π -π/2 0 π/2
Im
π
n
g(n)
⎜G (ω)⎜
x
-a
Re
-π -π/2 0
π/2
π
n
Fig. 13
L’operazione di decimazione o sottocampionamento nel tempo è lecita in quanto il segnale dopo i filtri ha
banda dimezzata. A questo proposito ricordiamo che per il teorema del campionamento un segnale filtrato
su metà banda, può essere rappresentato con metà dei campioni (per dimezzare il numero dei campioni si
usa appunto un decimatore a 2 punti).
Fig. 14
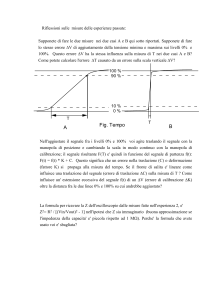
Il campionamento di segnali passa banda è regolato dalla seguente relazione:
f =
c
2f
max
m
, dove fc è la
f
frequenza di campionamento e m è il massimo intero non superiore a max .
B
Con riferimento alla Fig. 14, si può osservare che i segnali al primo livello vengono sottocampionati e
quindi la loro banda raddoppia; successivamente entrano nei filtri che hanno la stessa risposta impulsiva del
livello precedente. L’uscita dei filtri viene ancora sottocampionata e poi filtrata e tali operazioni si effettuano
su un numero di livelli stabilito da colui che esegue la decomposizione.
La decomposizone del segnale secondo Mallat è costituita dall'ultima sequenza di approssimazione e da
tutte le sequenze di dettaglio.
Ad ogni livello di decomposizione la risoluzione temporale del segnale si dimezza a causa del
sottocampionamento a conferma che i segnali alle più basse frequenze hanno una risoluzione temporale più
bassa (ma nel rispetto del teorema di Nyquist) rispetto ai segnali ad alta frequenza. Di conseguenza la
risoluzione in frequenza è più elevata.
In Fig. 15 è riportato un esempio di decomposizione di un segnale chirp con rumore su un tratto
temporale breve (prima riga), con i dettagli sulla colonna di destra e le approssimazioni a sinistra.
Fig. 15
In Fig. 16 è riportato un esempio di decomposizione su tre livelli, con la rappresentazione temporale e
frequenziale: il segnale da decomporre appare in alto in (a), la cui banda è riportata in alto sulla colonna (b);
in (a) e in (b) sono anche mostrati rispettivamente i segnali e i relativi spettri decomposti ai vari livelli.
(a)
(b)
Fig. 16
Notare che lo spettro in figura schematizza la suddivisione in sottobande del segnale, ma non riflette il
contenuto spettrale (in particolare la risoluzione frequenziale) dei segnali ai diversi livelli di suddivisione
che si ottiene per effetto dell’applicazione dell’algoritmo di Mallat.
Prendiamo ora in esame il processo di ricostruzione del segnale, che prevede ad ogni passo:
a) un’interpolazione di un fattore 2,
b) la convoluzione con i filtri di ricostruzione (uguali a quelli utilizzati nella decomposizione);
c) la somma delle sequenze risultanti.
Ricordiamo che per interpolazione si intende la procedura di inserimento di punti in una sequenza per
simulare l’aumento della frequenza di campionamento; questi campioni aggiuntivi sono in genere scelti
nulli.
Ciscun livello di ricostruzione è descritto dalla seguente relazione:
x[ n] = ∑ ∑ ⎧⎨ y high [ j , k ] ⋅ g [ n − 2 j k ] + ylow [ j , k ] ⋅ h[ n − 2 j k ]⎫⎬ .
⎭
jk⎩
In Fig. 17 è riportato lo schema a blocchi dell’algoritmo di decomposizione e ricostruzione di un segnale.
.
Fig. 17
L’interpolazione temporale di un fattore ‘2’ effettuata sul segnale ‘dettaglio’ restituisce la risoluzione
temporale dello stesso prima della decimazione. La successiva convoluzione tra il segnale interpolato e il
filtro (g[n] o h[n]) permette di riottenere il segnale al livello precedente la decomposizione.
1.1.1.2
Algoritmo senza decimazione
Le operazioni di sottocampionamento presenti nell’algoritmo di Mallat eliminano la ridondanza nella
rappresentazione del segnale, ma causano la diminuzione della risoluzione temporale all’aumentare del
livello di decomposizione. In alcune applicazioni può essere importante mantenere la stessa risoluzione
temporale su tutti livelli.
Per rispondere a tale esigenza è stato sviluppato un algoritmo di decomposizione senza decimazione nel
tempo. La decomposizione del segnale avviene ancora facendo passare il segnale attraverso due filtri g[n] e
h[n], rispettivamente passa-alto e passa-basso. Tuttavia, nell’algoritmo senza decimazione gli stadi di
sottocampionamento sono rimossi, mentre le risposte impulsive dei filtri sono interpolate ad ogni livello di
decomposizione. L’interpolazione nel tempo equivale alla decimazione dei campioni frequenziali.
Pertanto, a differenza dell’algoritmo di Mallat, i filtri hanno diversa risposta impulsiva ai diversi levelli di
decomposizione.
Indicando con h[n] la generica risposta impulsiva del filtro passa basso, la risposta impulsiva hk[n] al
livello k è ottenuta inserendo ( 2 k − 1 ) zeri fra ciascun coppia di coefficiente di h[n]:
⎧ ⎛ n ⎞
⎟
n = 2k − 1m
⎪h⎜
h ( n) = ⎨ ⎜ k − 1 ⎟
⎝2
⎠
k
⎪ 0
altrimenti
⎩
dove m = 0,1,….,L - 1 è la lunghezza del filtro. Per il primo livello si ottiene: h1(n) = h(n).
La relazione tempo-frequenza porta alla seguente formula:
⎧⎪ ⎛ n ⎞⎪⎫ 2 k − 1
j 2 k − 1ω )
⎟⎬ =
(
F ⎨h⎜⎜
H
e
2π
⎪⎩ ⎝ 2 k − 1 ⎟⎠⎪⎭
jω
’, formalismo utilizzato nelle rappresentazioni
dove l’argomento ‘ω’ di H è stato sostituito con ‘ e
discrete. In modo analogo si procede per il filtro passa-alto.
Lo schema di funzionamento dell’algoritmo di decimazione in frequenza è riportato in Fig. 18. Con tale
algoritmo bisogna anche tener conto del diverso ritardo introdotto dai filtri ai vari livelli di decomposizione
a causa della diversa durata temporale della risposta impulsiva. All’aumentare del livello di decomposizione
il ritardo temporale introdotto dai filtri aumenta e di ciò bisogna tenere conto nella localizzazione temporale
di un evento.
x[n]
g[n]
h[n]
Coefficienti
g[n/2]
h[n/2]
Coefficienti
g[n/4]
Coefficienti
h[n/4]
Coefficienti
Fig. 18
A titolo di esempio, supponiamo di utilizzare come wavelet madre una ‘spline’ quadratica, la cui
trasformata di Fourier è data da:
4
⎛ ⎛ω ⎞⎞
⎜ sin⎜ ⎟ ⎟
⎝ 4 ⎠⎟
Ψ (e jω ) = jω ⎜⎜
ω ⎟
⎜⎜
⎟⎟
⎝ 4 ⎠
Si può dimostrare che i filtri da usare nella decomposizione senza decimazione, sono dati dalle seguenti
espressioni delle risposte in frequenza:
H (e
G (e
jω
jω
)=e
ω⎞
jω / 2 ⎛
⎜ cos ⎟
2⎠
⎝
) = 4 je
3
jω / 2 ⎛ ω ⎞
⎜ sin ⎟
2⎠
⎝
le quali rappresentano due filtri FIR che partizionano lo spettro in due sottobande, le cui risposte
impulsive sono:
1
h[n] = {δ [ n + 2] + 3δ [ n + 1] + 3δ [ n] + δ [ n − 1]}
8
g[n] = 2{δ [ n + 1] − δ [n]}
Con riferimento allo schema a blocchi di Fig. 18 si può dimostrare che la risposta in frequenza Qk (e jω )
che compete al k-esimo livello di decomposizione è data da:
Q (e
k
jω
⎧G (e jω )
⎪⎪
)=⎨
j 2 k − 1ω k − 2
j 2l ω
), ∏ H (e
)
⎪ G (e
⎪⎩
l =0
k =1
k≥2
In particolare: per k = 1, la sequenza temporale viene filtrata solo dal filtro G() senza decimazione in
frequenza; quando k = 2, la sequenza temporale viene filtrata da un filtro H() senza decimazione in
frequenza e da un filtro G() con decimazione in frequenza. Proseguendo con k crescenti si completa la
decomposizione.
Tipiche risposte in frequenza per diversi valori di k sono riportate in Fig. 19. L’uscita del filtro al livello kesimo è il prodotto delle funzioni di trasferimento G() e H(), sulla base della precedente formula.
k=1
K=3
K=2
Fig. 19
In Fig. 20, vediamo come si presenta la trasformata wavelet del segnale ECG mediante l’algoritmo senza
decimazione, limitatamente ai primi cinque livelli di decomposizione: in (a) possiamo vedere come l’onda R,
approssimata con un’onda triangolare, generi una coppia di massimo-minimo locale lungo tutti i livelli (in
quanto l’onda R simulata ha un contenuto frequenziale esteso a tutta la banda frequenziale). Il picco
dell’onda R corrisponde al punto di attraversamento delle zero compreso fra il massimo e il minimo locale.
Fig. 20
L’onda T, mostrata nel caso (b) dopo il complesso QRS, presenta le componenti a maggiore ampiezza nei
livelli inferiori corrispondenti alle frequenze più basse (livelli 24 e 25). Se il segnale è disturbato da un rumore
ad alta frequenza (c), i livelli più influenzati sono quelli a frequenze più alte (principalmente il 21 e 22); un
rumore più lento che distorce la linea base (d), per esempio un artefatto da movimento, influenza solo i
livelli inferiori (maggiori di 24).
Ai fini di una localizzazione più accurata del picco R è necessario considerare il ritardo temporale
introdotto dai filtri, il quale aumenta al crescere del numero di livelli (in quanto la lunghezza del filtro
aumenta in durata temporale).
L’algoritmo di decimazione in frequenza si presta anche per essere implementato via hardware in modo
semplice, per filtrare un segnale sulla banda frequenziale k-esima, preservando la massima risoluzione
temporale compatibile con il teorema del campionamento del segnale.
12/01/2011
1.1.2
Trasformata wavelet bidimensionale
L’estensione al caso 2D della TWC monodimensionale passa attraverso la seguente trasformazione. Data
la funzione 2D f(x,y), la sua TWC-2D è definita come:
⎛ x −τ
y −τ ⎞
⎜
1
y⎟
x,
⋅ ∫∫ f ( x, y ) ⋅ Ψ * ⎜
TWC (τ ,τ , s ) =
⎟dxdy
1 2
s ⎟
⎜ s
s
⎝
⎠
Una soluzione più pratica per applicare la decomposizione wavelet a immagini può essere ricavata
mediante l’impiego di filtri con un algoritmo analogo a quello di Mallat. Nel caso bidimensionale è
necessario distinguere due soluzioni, una basata sull’impiego di filtri non separabili e l’altra su filtri
separabili.
In Fig. 21 è riportato lo schema di principio della suddivisizione in livelli di un’immagine utilizzando
filtri non separabili.
Fig. 21
Il termine x(n,m) indica la matrice dell’immagine da analizzare, i filtri G(.,.) e H(.,.) sono gli equivalenti
bidimensionali rispettivamente dei filtri passa basso e passa alto nel caso 1D; il decimatore D deve essere
inteso nelle righe e nelle colonne della matrice dell’immagine, l’operazione che lega l’ingresso con l’uscita di
ciascun filtro è la conoluzione bidimensionale.
Come esempio di filtro passa-basso consideriamo un filtro circolarmente simmetrico, avente la risposta in
frequenza del tipo:
H (e
jω1
,e
jω 2
) =
⎧⎪1
⎨
⎪⎩0
2
2
2
2
ω 1 +ω 2 ≤ ω c
ω 1 +ω 2 > ω c
dove ω c è la pulsazione di campionamento. Un esempio di filtro passa-alto si ottiene sostituendo il segno
‘<’ con ’>’ nella precedente formula.
La soluzione basata su filtri non separabli suddivide lo spettro dell’immagine in sottobande in maniera
isotropica, senza quindi la capacità di estrarre informazioni di natura direzionale. Nella pratica tale metodo
viene applicato nell’analisi frattale, dove le forme differiscono essenzialmente per la dimensione non per
l’orientazione, e nell’analisi della tessitura di un’immagine ovvero nell’analisi dell’organizzazione spaziale
dei livelli di grigio.
E’ anche possibile applicare la decomposizione wavelet ad un’immagine sfruttando la proprietà di
separabilità di un filtro 2D in due filtri 1D, cioè tale che se w(x,y) è la risposta spaziale del filtro, si possa
scrivere φ (x,y) = φ (x) φ (y). I filtri φ (x) e φ (y) vengono applicati rispettivamente alle righe e alle colonne
dell’immagine con una sequenza opportuna come illustrato in Fig. 22. A ciascuna livello di decomposizione
si ottengono: un’immagine passa-basso (LL) e tre immagini ciascuna corrispondente alla direzione
orizzontale (LH), verticale (HL) e diagonale (HH). Le sottobande sono prodotte mediante operazioni di
filtraggio seguite da operazioni di sottocampionamento con fattore 2.
Fig. 22
Il banco di filtri di ricostruzione è riportato in Fig. 23.
Fig. 23
L’immagine passa-basso (LL) potrà essere ulteriormente decomposta in altre quattro immagini secondo
lo schema appena esposto.
LL
LL
HL
LH
HH
HL
HL
LH HH
LH
HH
(a)
(b)
Fig. 24
Come descitto in Fig. 24a, la decomposizione trasforma l’immagine in un segnale medio o
approssimazione e in tre segnali dettaglio sensibili alla direzione: LH evidenzia le caratteristiche orizzontali
dell’immagine, HL quelle verticali, HH quelle diagonali; in Fig.24b è riportato un esempio di
decomposizione su tre livelli per l’immagine del quadrante in alto a sinistra. In termini di numero di pixels,
si generano quattro sottoimmagini di dimensioni pari ad un quarto della matrice dell'immagine originale
che messe insieme restituiscono la dimensione di partenza.
Si può osservare che, in generale, nei riquadri dei dettagli orizzontali, verticali e diagonali, siamo in
presenza di una gran quantità di pixel la cui ampiezza è prossima allo zero, che possono essere eliminati
come succede nell’operazione di compressione.
Fig. 25
Si può anche eliminare il contributo dell’approssimazione quando l’obiettivo della TWD è valutare
l’effetto del filtraggio passa alto, ottenendo risultati del tipo di Fig. 25 che riporta il risultato
dell’eliminazione del contributo di appropssimazione (riquadro in basso a destra).
1.1.3
Applicazioni
1.1.3.1
Denoising
Un obiettivo importante della scomposizione wavelet è l’applicazione, nel dominio wavelet, di filtri di
denoising in modo da ripulire l’immagine (o il segnale) dal rumore. Si tratta di filtrare i coefficienti wavelet
d o(k) (a ciascun livello j, posizione spaziale k e orientazione) che hanno basso SNR.
j
Un metodo per stabilire la soglia di filtraggio nel dominio wavelet consiste nell’applicare la seguente
formula:
2
2⎞
⎛
⎜ ⎛⎜ do (k) ⎞⎟ − 3⎛⎜ σo (k) ⎞⎟ ⎟
j ⎠
⎝ j ⎠ ⎟
α = ⎜⎝
⎜
⎟
2
⎛⎜ do (k) ⎞⎟
⎜
⎟
⎝ j ⎠
⎝
⎠
o
dove α è il filtro che minimizza l’errore quadratico medio per ciascun coefficiente. Il termine ⎛⎜ σ (k) ⎞⎟
⎝
j
2
⎠
2
rappresenta la varianza del coefficiente osservato, mentre il termine ⎛⎜ d oj (k ) ⎞⎟ rappresenta il quadrato del
⎝
⎠
valore del coefficiente wavelet. Il valore di α è nullo quando il numeratore assume valore negativo.
L’operazione di de-noising consiste nel moltiplicare i coefficienti della scomposizione wavelet per il
valore di α , al variare di k.
In presenza di rumore additivo gaussiano bianco e assumendo che la varianza del rumore sia costante su
tutto il dominio dei coefficienti e valga σ 2 , il filtro α assume la forma semplificata ottenuta con la seguente
2
o
j
sostituzione: σ (k) = σ . Ovviamente si deve conoscere a priori o poter stimare il valore di σ .
Un modo alternativo all’applicazione della precedente formula è quello di fissare una soglia ad un valore
2
proporzionale a σ e di azzerrare i coefficienti che non superano la soglia.
L’ipotesi che supporta l‘operazione di denoising è che la banda del segnale è meno estesa della banda del
rumore e quindi l’energia del rumore viene ripartita su un numero maggiore di coefficienti di quanto accada
per il segnale, con il conseguente miglioramento dell’SNR sulle bande del segnale.
17/01/2011
Esercitazione: implementazione dell’algoritmo di Mallat. Partendo dal segnale ECG misurato, effettuare i
seguenti passi
o
sommare rumore bianco al segnale ECG
o
applicare l’algoritmo di Mallat ed effettuare l’operazione di de-noising utilizzando il filtro α e
l’operazione di sogliatura
o
calcolare l’errore quadratico medio tra il segnale senza rumore e il segnale filtrato e discutere i
risultati
o
implementare l’algoritmo senza decimazione
o
applicare l’algoritmo senza decimazione al segnale ECG con rumore
o
valutare il ritardo introdotto all’aumentare dei livelli di decomposizione
1.1.3.2
Compressione
In generale quando si parla di compressione si deve innanzitutto capire quando sia possibile comprimere
un’immagine. Per fare ciò è necessario dare alcune definizioni.
Un’immagine può essere considerata alla stregua di una sorgente discreta con un alfabeto A di M
simboli. Per esempio, nel caso di un’immagine, i simboli sono M = 256 e corrispondono ai livelli di grigio. Il
j-esimo simbolo, con j = 1,....,M , ha probabilità pj di essere generato.
La corrispondente informazione per simbolo è definita dalla seguente relazione:
I
1
= log 2
j
pj
cioè l’informazione è tanto più grande quanto minore è la probabiltà che ha il simbolo di essere generato.
Per esempio, in un contatore binario, i bit meno significativi si ripetono più frequentemente di quelli più
significativi, ma un errore in questi ultimi è di gran lunga più pesante.
L'informazione contenuta nell'immagine è la somma dell’informazione dei singoli simboli ed è data dalla
seguente relazione:
M
1
I = ∑ log 2
j =1
pj
La base teorica della riduzione dei dati si può ricondurre al primo teorema di Shannon che afferma che
una sorgente S che emette M simboli s1,.....,sM con rispettive probabilità p1,....,pM (indipendenti) può essere
caratterizzata dal valor medio (valore atteso) dell'informazione per simbolo o entropia. Il riferimento per
decidere se una sorgente può essere compressa è data proprio dal valore dell’entropia.
L’entropia, o valor medio statistico dell'informazione per simbolo, è data da:
M
1
H ( s ) = ∑ p log 2
j =1 j
pj
H(s) viene espressa in numero medio di bit di informazione/simbolo.
Pertanto, data una sorgente di informazioni con i simboli statisticamente indipendenti sottoposta ad
operazioni sui singoli pixels, al variare delle probabilità dei simboli l’entropia risulta massima per simboli
equiprobabili. Infatti, per simboli equiprobabili si ha che pj = 1/M e quindi:
Hmax = log M
che rappresenta il massimo dell’entropia. Quindi l'entropia di una sorgente di M simboli varia fra zero e
logM al variare della probabilità dei singoli simboli. Le sorgenti a simboli equiprobabili utilizzano al meglio
le possibilità dei caratteri di cui dispongono.
Si ha ridondanza quando l'entropia H di una sorgente è minore della massima Hmax consentita
dall'alfabeto. Quando ciò accade, ha senso procedere alla compressione delle immagini.
La TWD è una delle tecniche di compressione attualmente tra le più usate. Tra le caratteristiche che la
rendono efficace ai fini della compressione vi sono la preoprietà di conservazione dell’energia, la quale viene
mediamente concentrata in un ridotto numero di coefficienti nella rappresentazione multirisoluzione
(proprietà di decorrelazione e compattazione di energia), e inoltre i contorni e le discontinuità hanno una
rappresentazione compatta (generano un limitato numero di coefficienti nelle varie sottobande di dettaglio).
Tali proprietà consentono di localizzare su un numero ridotto di coefficienti la maggior parte di energia di
un’immagine, mentre i restanti coefficienti assumono valori prossimi allo zero. A questo punto, imponendo
una soglia minima, i coefficienti di bassa ampiezza possono essere forzati a zero.
In Fig. 26 è rappresentata una scomposizione al primo (a), secondo (b) e terzo livello (c).
(a)
(b)
Fig. 26
(c)
La necessaria riduzione di occupazione di memoria, e quindi la compressione, è ottenuta facendo seguire
all’operazione di TWD, un’operazione di codifica che riduca il numero di codici necessari per rappresentare
stringhe di simboli di valore uguale. Infatti, può essere conveniente sostituire alla codifica dei singoli simboli
quella del primo simbolo seguita da un numero che indichi il numero dei simboli successivi se uguali. La
codifica ‘run-length’ realizza tale algoritmo.
Quindi la codifica run-length è utile quando vi siano più caratteri dominanti che si presentano con
un'incidenza statistica maggiore di una determinata soglia. Ad esempio si abbia la seguente sequenza:
1,200,0,0,0,0,0,0,0,134,134, che si comprime nella: 1,200,∼,0,7,134,134, dove il carattere ∼ ha il ruolo di carattere
speciale e viene seguito dal carattere che si vuole comprimere seguito dalla sua numerosità. Evidentemente
la soglia in questo caso è 3, mentre sono sempre 3 le celle necessarie per rappresentare la codifica; infatti i
caratteri 134,134 non sono stati compressi.
Esercitazione: implementazione dell’algoritmo TW-2D
-
realizzare le seguenti maschere spaziali, calcolarne il contenuto frequenziale e discutere la tipologia di
filtro
-1
-1
-
-1
-1
2
-1
2
-1
2
-1
-1
2
2
2
-1
2
-1
-1
2
-1
-1
2
-1
-1
-1
-1
2
-1
-1
-1
2
-1
-1
-1
2
orizzontale
-
-1
+ 45°
verticale
- 45°
applicare le suddette maschere all’immagine di Fig. 24b (in alto a sinistra) per acquisire conoscenze sul
filtraggio direzionale
utilizzando la funzione matlab ‘wavedec2’ applicare la TW-2D all’immagine di cui sopra e interpretare i
risultati
aggiungere rumore all’immagine e implementare il filtraggio di denoising 2D