Esami di Fisica Generale I e II con Lab e Fisica

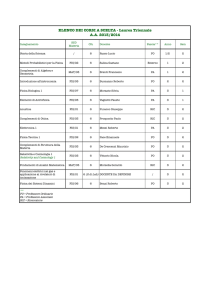
Corso di Laurea in Ingegneria Meccanica
A.A. 2012/2013, Sessione Estiva
Esami di Fisica Generale I e II con Lab e Fisica Generale I e II
27 Giugno 2013, Prova Scritta
RISOLVERE I SEGUENTI PROBLEMI
PROBLEMA 1 (Fis. Gen. I Lab.)
Una massa di un gas perfetto di massa molecolare A ruota intorno ad un asse verticale con velocità
angolare ω . A partire dalla statistica di Boltzmann, calcolare la densità del gas al variare della
distanza r dall’asse di rotazione.
Soluzione
La statistica di Boltzmann è:
dn
=
N
in cui: ε =
e
∫e
−
ε
kT
−
ε
kT
dxdydz 4π p 2dp ,
dxdydz 4π p 2dp
1
1
1
mv 2 − mω 2 r 2 . Il termine − mω 2 r 2 è l’energia potenziale dovuta al campo di forza
2
2
2
centrifuga.
Sostituendo questa espressione dell’energia nella formula di Boltzmann, integrando su tutto lo
spazio degli impulsi, ricordando che la distribuzione è normalizzata, si ha:
mω 2 r 2
2 kT
2 2
2 2
mω r
mω r
dn
e
dxdydz
d ( mn)
Nm
= mω 2r 2
⇒
= mω 2r 2
e 2 kT ⇒ ρ ( r ) = ρ 0e 2 kT ,
N
dV
2
2
∫ e 2kT 4π r dr
∫ e 2kT 4π r dr
in cui abbiamo:
Nm
.
ρ 0 = mω 2 r 2
∫e
2 kT
4π r 2 dr
Questa è la stessa formula trovata con la legge dei gas perfetti in un precedente esame.
PROBLEMA 2 (Fis. Gen. I Lab. e Fis. Gen. I)
Le equazioni parametriche del moto di un punto materiale sono:
! x(t ) = a cos t
"
1 + sin t
#
"% y (t ) = a(ln cos t ) − a sin t
Trovare l’equazione della traiettoria.
Soluzione
Sostituendo si ottiene: y( x) = a ln
a + a2 − x2
− a 2 − x 2 , si tratta di una “trattrice”.
x
PROBLEMA 3 (Fis. Gen. I Lab. e Fis. Gen. I)
Un automobile con una massa di 700kg rallenta dalla velocità di 120km / h in autostrada a quella
di passaggio in un casello Telepass di 30km / h . Calcolare l’energia che i freni devono smaltire.
Se supponiamo che la frenata avvenga in uno spazio h = 100m , con accelerazione costante,
calcolare il tempo di frenata e l’andamento della velocità in funzione del tempo durante la manovra.
Supponiamo adesso che il freno sia in realtà un’apparecchiatura elettrica che trasforma l’energia,
altrimenti persa, della frenata in una corrente elettrica a 12V che ricarica la batteria. Dare
l’andamento di tale corrente in funzione del tempo e calcolare la corrente all’istante in cui comincia
il rallentamento ( t = 0 ).
Soluzione
L’energia da smaltire è uguale alla variazione di energia cinetica dell’auto:
1
ΔT = m(v02 − v 2f ) = 350(33,32 − 8,32 ) = 364kJ .
2
1
Le equazioni del moto durante il rallentamento sono: s = v0t − at 2 e v = v0 − at .
2
Se la frenata dura Δt , abbiamo:
v0 − v f
1
.
h = v0 Δt − aΔt 2 e
a=
2
Δt
Da queste due equazioni ricaviamo il tempo di frenata:
2h
Δt =
= 4,8s
v0 + v f
e l’accelerazione:
v f − v0
v02 − v f 2
a=
=−
= −5, 2ms −2 .
Δt
2h
La velocità dell’auto in funzione del tempo sarà pertanto:
v = v0 + at = 33,3 − 5, 2 ⋅ t
1
e la sua energia cinetica: T = m(v0 + at )2 , da cui ricavo la perdita di energia per unità di tempo:
2
v02 − v f 2 v02 − v f 2
dT
.
= m(v0 + at )a = −m(v0 −
t)
dt
2h
2h
Eguagliando questa potenza (cambiata di segno) a quella prodotta dal generatore, abbiamo:
dT
−
= Vi (t ) . Da cui ricaviamo l’andamento della corrente in funzione del tempo:
dt
v02 − v f 2 v02 − v f 2
m
.
i (t ) = (v0 −
t)
V
2h
2h
Sostituendo i numeri, si ha: i(t ) = 303,33(33,3 − 5, 2t ) e i(0) = 303,3i33,3 = 10101A .
PROBLEMA 4 (Fis. Gen. I)
Un elettrone entra al centro della zona di spazio tra le armature di un condensatore piano; la velocità
iniziale dell’elettrone è v0 = 5 ⋅105 m / s , la distanza fra le armature è d = 40 cm, mentre la loro ddp
è ΔV = 2 V. Si calcoli la distanza che l’elettrone percorre prima di colpire l’armatura (
e = 1,6 ⋅10−19 C , m = 9,1⋅10−31 kg ).
Soluzione
Il movimento trasversale alle armature è uniformemente accelerato con accelerazione:
d
md 2
eE eΔV d 1 2
; = at ⇒ t =
=
= 34 cm.
a=
=
2 2
a
eΔV
m
m
PROBLEMA 5 (Fis. Gen. II Lab.)
Nel discutere le oscillazioni di una corda di densità lineare ρ , ci siamo occupati solo delle
oscillazioni trasversali, perché la forza dovuta alla tensione T lungo la corda è piccola. Scrivere
comunque l’equazione differenziale delle oscillazioni dovute a T lungo la direzione della corda,
discuterne le caratteristiche e trovarne una soluzione per un’oscillazione trasversale di tipo
sinusoidale.
Soluzione
La forza lungo l’asse di propagazione è:
Fx = T cos α ( x + dx) − T cos α ( x) .
Sviluppando il coseno di α , cos α = 1 −
forza:
α2
2
, abbiamo per la componente orizzontale (X) della
" (α + dα )2 #
" α2 #
T %1 −
−
T
&
%1 − & = −Tα dα ,
2
2(
'
(
'
∂y ∂ 2 y
∂2 y
∂y
trascurando il termine in (dα )2 . Poiché α =
e dα = 2 dx , troviamo: −Tα dα = −T
dx
∂x
∂x ∂x 2
∂x
eguagliando questo alla massa per accelerazione di un pezzetto di corda di lunghezza infinitesima
∂y ∂ 2 y
∂ 2ξ
∂y ∂ 2 y 1 ∂ 2ξ
,
ovvero:
dx e densità lineare ρ , abbiamo: −T
dx
=
ρ
dx
+
= 0 , con ξ lo
∂x ∂x 2
∂t 2
∂x ∂x 2 v 2 ∂t 2
1 ρ
spostamento dell’elementino di corda dalla posizione di riposo x , 2 = .
v
T
∂y
Si vede che la forza è nulla, se
= 0 , in questo caso il trattino di corda è orizzontale e le tensioni
∂x
∂2 y
a destra e a sinistra sono allineate, oppure se
= 0 . In questo caso la forma della corda è
∂x 2
localmente lineare e di nuovo le forze a destra e a sinistra dell’elementino di corda sono allineate.
Prendendo adesso una soluzione sinusoidale per y ( x, t ) : y ( x, t ) = A cos(kx − ωt ) e sostituendo
abbiamo:
1 ∂ 2ξ
A2 k 3 cos(kx − ωt )sin(kx − ωt ) = − 2 2 ,
v ∂t
ovvero:
1
1 ∂ 2ξ
λ
∂ 2ξ
.
cos(kx − ωt )sin(kx − ωt ) = sin 2(kx − ωt ) − 2 2 3 2 = − 2 2
2
v A k ∂t
ω A 2π ∂t 2
Facciamo ora una doppia integrazione sul tempo e otteniamo:
λ
∂ 2ξ
1
− 2 2
= − 2 sin 2(kx − ωt ) ,
2
ω A 2π ∂t
8ω
ovvero:
Aπ
ξ ( x, t ) = A
sin 2(kx − ωt ) .
λ 4
Da cui si vede che l’oscillazione longitudinale ha frequenza doppia e lunghezza d’onda metà
A
rispetto a quella trasversale, mentre la sua ampiezza è ridotta di un fattore
certamente molto
λ
minore di 1, per l’ipotesi che le oscillazioni trasversali siano piccole (altrimenti non si può dire che
sin α : α ). In effetti per la nostra onda abbiamo che α è massima quando kx − ωt = π2 , perché
∂y
A
allora α =
= Ak sin(kx − ωt ) sarà massima e di valore uguale ad Ak = 2π . Se, poniamo, α
∂x
λ
A 1
A
1
1
non deve eccedere il decimo di radiante (6 gradi), allora: 2π ≤ ⇒ ≤
. Ne segue
=
λ 10 λ 2π 10 62,8
che l’ampiezza di oscillazione lungo X sarebbe dell’ordine del due per cento dell’ampiezza di
oscillazione trasversale.
PROBLEMA 6 (Fis. Gen. II Lab.) Consideriamo la scarica di un condensatore piano di capacità
C (distanza tra le armature d e superficie delle armature S ' ) su un filo di lunghezza l , sezione S
e resistività ρ . Calcolare la corrente di spostamento all’interno del filo.
Soluzione
dx
La caduta di potenziale lungo un trattino infinitesimo di filo è: dV = ρ i da cui:
S
dV
i (t )
.
E=
=ρ
dx
S
l
S'
La densità di corrente di spostamento js è allora ( τ = RC = ρ ε 0 ):
S
d
d (ε 0 E )
ρε
ρε
ρε
1 di(t )
Sd
0
js =
= ρε 0
= − 0 i(t ) = − 0 jc (t ) = −
jc (t ) = −
jc (t ) .
l
S
'
dt
S dt
Sτ
τ
lS
'
ρ ε0
S d
d
Presumibilmente,
<< 1, ne segue che is << ic . In un precedente compito di esame abbiamo
l
mostrato che is = −ic , dove con is abbiamo indicato la corrente di spostamento attraversante le
armature del condensatore, senza tenere conto della corrente di spostamento lungo il filo. Adesso
d
dobbiamo modificare quel risultato, scrivendo: is = −ic (1 + ) , con is corrente di spostamento
l
totale.
PROBLEMA 7 (Fis. Gen. II Lab.) Un oscillatore armonico di massa m e costante elastica k si
trova nello stato fondamentale. Si calcoli la probabilità di trovarlo al di fuori della zona permessa
1
mω x 2
% mω & 4 − 2 h
classicamente (la funzione d’onda per lo stato fondamentale è: ψ 0 ( x) = '
).
( e
) πh *
Soluzione
La regione permessa classicamente è il segmento tra i due punti d’inversione del moto che hanno
2E
2E
coordinata ±ξ = ±
, come si vede notando che all’estremo del segmento l’energia è
=±
k
mω
1
solo potenziale e E = V (ξ ) = kξ 2 . In meccanica quantistica, la zona permessa si estende
2
all’infinito e la probabilità di trovare l’oscillatore in un qualsiasi punto è data dal modulo della
funzione d’onda al quadrato. La probabilità totale di trovarlo fuori della zona permessa
classicamente è la somma o integrale della funzione d’onda modulo quadro fuori del segmento
permesso. In formule:
1
$ mω ' 2 +∞ − mω x
P = ∫ ψ0 (x) + ∫ ψ0 (x) = 2 &
) ∫ e 2
% π ( ξ
−∞
+ξ
−ξ
=
dove
2
+∞
2 $ +∞ − y 2 2
&& ∫ e
dx −
π%0
2
1
∫
0
e− y
2
2
2
2
dx =
' 2 $ π
&
dx )) =
−
&
π% 2
(
1
∫
0
e− y
2
π
2
2
+∞
∫
e− y
2
2
dx =
1
'
dx )) = 1− 2Erf (1) = 0,16,
(
Erf (1) =
è la funzione errore che è tabulata.
1
π
1
−y
∫e
0
2
2
dx