Amplificatore a doppio carico

Esercitazione n° 4: Amplificatore a doppio carico
Esercitazione n° 4: Amplificatore a doppio carico
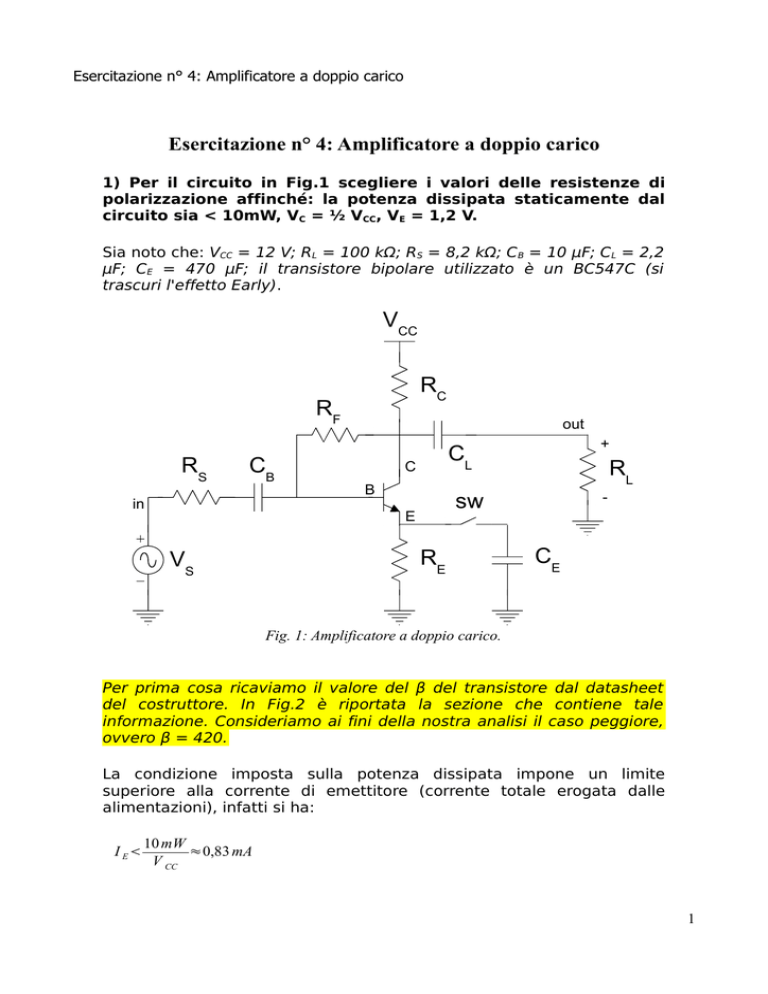
1) Per il circuito in Fig.1 scegliere i valori delle resistenze di
polarizzazione affinché: la potenza dissipata staticamente dal
circuito sia < 10mW, VC = ½ VCC, VE = 1,2 V.
Sia noto che: VCC = 12 V; RL = 100 kΩ; RS = 8,2 kΩ; CB = 10 μF; CL = 2,2
μF; CE = 470 μF; il transistore bipolare utilizzato è un BC547C (si
trascuri l'effetto Early).
VCC
RC
RF
RS
CB
in
out
C
B
RL
sw
E
VS
+
CL
RE
-
CE
Fig. 1: Amplificatore a doppio carico.
Per prima cosa ricaviamo il valore del β del transistore dal datasheet
del costruttore. In Fig.2 è riportata la sezione che contiene tale
informazione. Consideriamo ai fini della nostra analisi il caso peggiore,
ovvero β = 420.
La condizione imposta sulla potenza dissipata impone un limite
superiore alla corrente di emettitore (corrente totale erogata dalle
alimentazioni), infatti si ha:
I E<
10 mW
≈0,83 mA
V CC
1
Esercitazione n° 4: Amplificatore a doppio carico
A questo punto per mantenere un minimo di margine sulla condizione
imposta, scegliamo IE = 600 µA.
Fig. 2: Parte del datasheet del transistore bipolare BC547C.
Fig. 3: Amplificatore a doppio carico: circuito per l'analisi statica.
2
Esercitazione n° 4: Amplificatore a doppio carico
Per determinare il valore dei resistori della rete di polarizzazione
facciamo riferimento alla parte statica del circuito in esame (Fig. 3).
Scrivendo la LKT alla maglia di uscita si avrà:
V CC =RC ( I C +I B )+V C
Da cui ricaviamo RC come (si osservi che l'elevatissimo valore di β rende
IE ≈ IC):
RC =
V CC −V C
≈10 k Ω
1
I C (1+ )
β
Per il resistore di emettitore si avrà:
RE=
VE
=2 k Ω
IE
Il valore commerciale più prossimo risulta essere R E = 2,2 kΩ che porta
ad un valore di VE pari a 1,32 V.
Il resistore di Feedback resta vincolato dalla seguente equazione (LKT
alla maglia di ingresso):
V CC =RC I E + RF I B+V BE+V E
Tenendo conto che VC = ½ VCC, consegue che a sua volta RCIE = ½ VCC,
ottenendo:
RF=
V CC −V BE −V E −V CC /2
≈2,7 M Ω
IB
3
Esercitazione n° 4: Amplificatore a doppio carico
2) Per il circuito in Fig.1 determinare il guadagno di tensione a
piccolo segnale (alle medie frequenze) nell'ipotesi che
l'interruttore sw resti aperto.
Come prima cosa consideriamo il circuito equivalente a piccolo segnale
valido per l'analisi AC alle medie frequenze:
Fig. 4: Circuito equivalente a piccolo segnale valido alle medie frequenze.
Prima di procedere bisogna al calcolo dei parametri differenziali del
transistore bipolare nell'intorno del punto di lavoro:
g m=
IC
=24 mS
Vt
r π=
Vt Vt
β
= β= ≈8,33 k Ω
I B IC
gm
r o=
VA
=∞
IC
Risulta subito evidente la difficoltà nell'analisi del circuito introdotta
dalla presenza del resistore RF. Una possibilità per ridurre la complessità
del circuito ci viene fornita dal teorema di Miller riportato in Appendice
1.
Possiamo, quindi, pensare di utilizzare la trasformazione di Miller per
analizzare il nostro amplificatore. Per fare ciò bisogna analizzare per
prima il circuito base (senza la presenza di R F) per il calcolo del K. Per
fare ciò consideriamo il seguente circuito equivalente semplificato:
4
Esercitazione n° 4: Amplificatore a doppio carico
Fig. 5: Circuito equivalente per il calcolo del K.
Ricordiamo che il K è definito come il rapporto tra le due tensioni
riferite a massa dei nodi tra cui è posta R F. Quindi bisogna
valutare:
K=
vc
vb
E' facile osservare che:
v b=v π +v e
v c =−RC∥R L ( g m v π )
quindi si arriva alla seguente espressione:
K=
−RC∥R L ( g m v π )
v π +v e
Scrivendo un bilancio di correnti al nodo di emettitore otteniamo:
v
vπ
+g m v π = e
rπ
RE
da cui:
5
Esercitazione n° 4: Amplificatore a doppio carico
v e =v π R E ( g m+
R (β+1)
1
)=v π E
rπ
rπ
Andando a sostituire nell'espressione di K si ottiene:
K=
−RC ∥R L ( g m v π ) −RC ∥R L⋅g m
V
=
≈−4,42
v π +V e
R E (β+1)
V
1+
rπ
Ora è possibile calcolare le due componenti in cui si sdoppia RF:
R F1=
RF
=500 k Ω
1−K
R F2=
RF
=2,2 M Ω
1−1/ K
A questo punto possiamo riconsiderare il nuovo circuito equivalente:
Fig. 6: Circuito equivalente dopo la trasformazione di Miller.
Ora possiamo finalmente passare al calcolo del guadagno di tensione:
Av =
v o vo vπ
=
vs v π vs
La tensione di uscita risulta semplicemente pari a:
v o =−g m v π RC ∥R L∥R F2
6
Esercitazione n° 4: Amplificatore a doppio carico
Per la tensione di ingresso bisogna valutare il trasferimento di segnale
da vs all'ingresso del transistore. Valutiamo la resistenza equivalente
guardando a destra di RF1:
Nel calcolo del K abbiamo trovato che:
v e =v π R E ( g m+
1
)=i b RE (β+1)
rπ
e siccome:
v b=v π +v e =i b r π +i b RE (β+1)=i b (r π +R E (β+1))
Possiamo, quindi, rivedere la sezione di ingresso al seguente modo:
Fig. 7: Circuito equivalente per il calcolo dell'accoppiamento di ingresso.
Osserviamo che
R E (β+1)+r π ≈450 k Ω , quindi il parallelo con RF1 varrà:
R F1∥( r π +R E⋅(β+1))≈
(r π+ RE⋅(β+1))
=225 k Ω
2
Questa considerazione ci permette di affermare che:
R s≪ R F1∥(r π+ RE⋅(β+1))
per cui possiamo semplificare i calcoli trascurando Rs. Fatte queste
7
Esercitazione n° 4: Amplificatore a doppio carico
dovute considerazioni avremo che il legame tra vs e vπ sarà immediato
a partire dalla regola del partitore di tensione:
v s=v π +
R (β+1)
vπ
R E (β+1)=v π (1+ E
)
rπ
rπ
Siamo finalmente giunti al punto in cui è possibile scrivere agevolmente
il guadagno di tensione del nostro amplificatore come segue:
Av =
v o −g m v π RC∥RL∥R F2 −β RC ∥R L∥R F2
=
=
vs
R E (β+1)
r π +R E (β+1)
v π (1+
)
rπ
RC , RL ≪ RF2 ,
A questo punto, tenendo conto che
semplificare ancora di più il risultato ottenendo:
Av ≈
possiamo
−β RC∥RL
r π +R E (1+β)
Questo risultato è molto importante perché ci permette di affermare
che se r π ≪ R E (1+β) (cosa che si verifica quasi in tutti i casi pratici) il
guadagno dell'amplificatore a doppio carico risulta parti al rapporto tra
le due resistenze di collettore ed emettitore, svincolandone il valore da
tutti i parametri fisici del transistore bipolare e quindi rendendolo
immune alle variazioni parametriche del circuito.
Nel nostro caso otteniamo:
Av ≈−
RC ∥R L
V
≈−4,1 ≈12,23 dB
RE
V
E' interessante a questo punto verificare se le approssimazioni fatte
erano ben poste e di quanto incidono sul valore finale del guadagno di
tensione calcolato. A tale scopo riportiamo una simulazione SPICE del
circuito in questione.
8
Esercitazione n° 4: Amplificatore a doppio carico
Fig. 8: Diagramma di Bode ottenuto tramite simulazione SPICE.
Dal diagramma di Bode ottenuto tramite simulazione SPICE otteniamo
un valore del guadagno a centro banda di 12 dB, ovvero circa -3,93 V/V
che è perfettamente in accordo con il valore ottenuto con il calcolo
analitico approssimato.
3) Calcolare il valore della resistenza di ingresso e di uscita del
circuito in Fig.1 nell'ipotesi che l'interruttore sw resti aperto.
Per il calcolo della resistenza di ingresso, non dobbiamo aggiungere
molto all'analisi già fatta durante il calcolo del guadagno di tensione.
Infatti abbiamo appurato che l'ingresso del nostro amplificatore può
essere visto come in Fig. 7, per cui risulta immediato scrivere che:
Rinput =R F1∥(r π +R E (β+1))≈
(r π +R E (β+1))
=225 k Ω
2
Il calcolo della resistenza di uscita risulta molto più complicato dalla
presenza di RF, infatti prendiamo in considerazione il circuito
equivalente utile al calcolo della resistenza di uscita:
9
Esercitazione n° 4: Amplificatore a doppio carico
Fig. 9: Circuito equivalente per il calcolo di Rout.
In questo caso non è possibile utilizzare la trasformazione di Miller 1. Per
valutare la resistenza di uscita si farà quindi uso della teoria dei sistemi
reazionati. Infatti il resistore RF introduce una reazione di tipo paralleloparallelo ed il doppio bipolo che identifica il blocco β è mostrato nella
Fig. 10. Il modello adatto a schematizzare il blocco β, in Fig. 11, è
quello a parametri G.
Applicando le definizioni dei parametri G, otteniamo:
G 11=
i1
v1
∣
=
1
RF
G 22=
i2
v2
∣
=
1
RF
v2=0
v1=0
β=G 12=
i1
v2
∣
v1=0
=−
1
RF
A questo punto è possibile inserire gli effetti di carico introdotti dalla
rete β e calcolare il guadagno di transresistenza come:
Ar =
vo
is
1 Infatti se togliessimo la resistenza RF tra base e collettore annulleremmo la porzione di corrente che da vx scorre
attraverso RF e ripartita tra Rs ed rπ crea una caduta di potenziale su rπ che a sua volta impone una corrente nel
generatore controllato in tensione del modello equivalente del bjt.
10
Esercitazione n° 4: Amplificatore a doppio carico
Fig. 10: Circuito per l'individuazione del blocco β.
Fig. 11: Modello equivalente della rete β.
Lasciamo al lettore la verifica delle seguenti relazioni (si faccia
riferimento al circuito di Fig. 12, dove il generatore di segnale in
ingresso è stato sostituito con il suo equivalente di Northon, trattandosi
di un amplificatore di transresistenza ):
11
Esercitazione n° 4: Amplificatore a doppio carico
Fig. 12: Circuito equivalente dell'amplificatore base con gli effetti di carico.
v π =i s
Rs∥R F
r
R s∥R F +[r π +R E (β+1)] π
v o=−g m v π R F∥RC ∥R L
v π ≈v s
rπ
r π +R E (β+1)
Quindi si ottiene:
Ar =
v o vo vπ
=
≈−32 k Ω
is vπ is
A questo punto è finalmente possibile calcolare la resistenza di uscita
come:
Rof =
Ro
1+ Ar β
dove:
Ro= RC∥RF
In definitiva:
Rof ≈
RC
=9,88 k Ω
32 k Ω
1+
RF
12
Esercitazione n° 4: Amplificatore a doppio carico
Ora è possibile valutare questo risultato anche con una simulazione
SPICE. In Fig. 13 è riportato lo schematico realizzato in LTspice IV per la
valutazione del guadagno di transresistenza, seguito (in Fig. 14) dal
risultato della simulazione.
Fig. 13: Schematico in LTspice IV utile alla valutazione del guadagno di transresistenza.
Fig. 14: Risultato della simulazione SPICE per il calcolo del guadagno di transresistenza.
13
Esercitazione n° 4: Amplificatore a doppio carico
Come è possibile osservare, il risultato della simulazione è in perfetto
accordo con il valore ottenuto per via analitica. Nelle figure successive
(Fig. 15-16) vengono riportati rispettivamente lo schematico utilizzato
per valutare la resistenza di uscita ed il risultato della simulazione
SPICE. Il risultato ancora una volta conferma l'esattezza dei risultati.
Fig. 15: Schematico in Ltspice IV utile alla valutazione della resistenza di uscita.
Fig. 16: Risultato della simulazione SPICE per il calcolo della resistenza di uscita.
14
Esercitazione n° 4: Amplificatore a doppio carico
4) Determinare la risposta in frequenza dell'amplificatore in
Fig.1 nell'ipotesi che l'interruttore sw resti aperto.
Dal datasheet riportato in Fig.2 ricaviamo i valori di CEB0 = 11 pF, CCB0 =
1,5 pF. Questi sono i valori calcolati in determinate condizioni
(sappiamo che tali capacità dipendono dal punto di lavoro del
transistore) ma ai fini di una valutazione approssimata della banda
passante li utilizziamo anche nel nostro caso.
Per prima cosa consideriamo il circuito equivalente per l'analisi in
frequenza, dove sono riportati gli elementi capacitivi interni ed esterni
al transistore bipolare.
Fig. 17: Circuito equivalente per l'analisi in frequenza.
Cominciamo con l'analisi in alta frequenza. Utilizziamo il metodo delle
costanti di tempo a circuito aperto. A tal fine consideriamo dei cortocircuiti le capacità di accoppiamento (C S e CL) e calcoliamo le costanti di
tempo associate alle capacità interne al bjt. Per la capacità Cμ si utilizza
la trasformazione di Miller già vista per R F. Si osservi che l'impedenza
associata ad una capacità si esprime come:
ZC =
1
j ωC
Quindi andando a sostituire nelle espressioni di Miller otteniamo:
Z 1=
Z
→C μ '=C μ(1−K )≈8,1 pF
1−K
analogamente:
15
Esercitazione n° 4: Amplificatore a doppio carico
C μ ' '=C μ (1−
1
)≈1,84 pF
K
Il circuito equivalente alle alte frequenze si ridisegna al seguente modo:
Fig. 18: Circuito equivalente per l'analisi in alta frequenza dopo la trasformazione di
Miller.
Cominciamo con il valutare la costante di tempo associata alla capacità
Cπ: a tal fine sostituiamo le capacità C μ' e Cμ'' con dei circuiti aperti e
valutiamo la resistenza equivalente vista ai capi di C π. Il circuito da
analizzare è riportato in Fig. 19:
Fig. 19: Circuito equivalente per la valutazione della resistenza equivalente vista dalla
capacità Cπ.
Ricordando l'analisi fatta per il calcolo della resistenza di ingresso (fare
riferimento alla Fig. 7) è facile ottenere il seguente circuito equivalente:
16
Esercitazione n° 4: Amplificatore a doppio carico
Fig. 20: Circuito equivalente semplificato per la valutazione della resistenza equivalente
vista dalla capacità Cπ.
A questo punto è facile valutare che:
ReqC π=[ RS∥RF1+R E (β+1)]∥r π≈r π=8,33 k Ω
Che porta a:
τ C π≈C π⋅r π≈0,91 ns
Per quanto riguarda Cμ', “apriamo” Cπ ed Cμ'': alla sua destra vedremo la
resistenza di ingresso del bjt, mentre a sinistra vedremo il parallelo tra
RF ed Rs, quindi:
ReqC μ ' =R S∥R F1∥(r π +R E⋅(β+1))≈ R S=8,2 k Ω
Quindi la costante di tempo associata a Cμ' diviene:
τ Cμ ' ≈C μ '⋅R S ≈0,66 ns
Cμ'' vedrà ai suoi capi la resistenza di uscita dell'amplificatore con in
parallelo RL, quindi:
τ Cμ ' ' ≈C μ ' ' (RC∥R L )≈0,16 ns
Da quanto ottenuto ci rendiamo conto che non è presente una costante
di tempo dominante, quindi non possiamo stimare la frequenza di taglio
superiore a 3dB. In ogni caso la frequenza di taglio che interviene per
prima è quella legata alla capacità C π, equivalente ad una frequenza di
17
Esercitazione n° 4: Amplificatore a doppio carico
f≈
1
=1,73 MHz .
2 π τC π
Passiamo ora allo studio del comportamento in bassa frequenza.
Utilizziamo il metodo delle costanti di tempo in corto-circuito. Tale
metodo prevede di sostituire con dei circuiti aperti le capacità interne al
transistore (Cπ e Cμ) e valutare le costanti di tempo associate alle
restanti capacità (CS, CL). Il circuito equivalente da considerare è
riportato in Fig. 21:
Fig. 21: Circuito equivalente per l'analisi in bassa frequenza.
La capacità CS (quando CL è un corto-circuito) vede ai suoi capi la
resistenza di ingresso dell'amplificatore più RS, quindi tenendo conto del
calcolo fatto nel punto 3 si ottiene:
τCS ≈C S⋅( R S +RF1∥( r π +R E⋅(β+1)))=2,33 s
Di contro la capacità CL (quando CS è un corto-circuito) vede ai suoi capi
la resistenza di uscita dell'amplificatore:
τCL≈C L⋅(R L +RC )≈0,242 s
In questo caso c'è una costante di tempo dominante alle basse
frequenze legata a CL, dando come risultato:
f
L3dB
≈
1
≈0,66 Hz
2 π τC
L
I risultati ottenuti sono pienamente confermati da una simulazione
spice, che ci permette di ottenere il diagramma di Bode già riportato in
Fig. 8 precedentemente.
18
Esercitazione n° 4: Amplificatore a doppio carico
5) Valutare qualitativamente cosa accade se l'interruttore sw
viene chiuso.
Se l'interruttore sw viene chiuso, da un punto di vista statico nulla
cambia. Infatti esso si trova posto in parallelo alla resistenza di
emettitore, non cambiando di fatto la polarizzazione del circuito.
Da un punto di vista dinamico bisogna fare un analisi di tipo asintotica.
Per basse frequenze (f → 0), accade che l'influenza di CE è del tutto
trascurabile essendo la sua impedenza molto grande (Z CE → ∞). Quindi il
comportamento resta identico al caso in cui l'interruttore è aperto. Per
frequenze “molto grandi” (f → ∞; ZCE → 0) succede che tale capacitore
cortocircuita il resistore RE, riportando il circuito di partenza ad una ben
nota configurazione ad emettitore comune. In tal caso si avranno i
seguenti risultati.
Il guadagno di tensione dell'amplificatore aumenta notevolmente,
infatti avevamo trovato che:
Av ≈
−β RC∥RL
r π +R E (1+β)
Se facciamo tendere a zero RE, otteniamo la ben nota relazione:
Av ≈−g m RC∥R L≈−216
V
V
La resistenza di ingresso diviene semplicemente:
Rinput =R F1∥r π≈8,33 k Ω
La resistenza di uscita resta praticamente immutata pari ad:
Rout ≈ RC =10 k Ω
In alta frequenza avremo che aumentando di un ordine di grandezza il
guadagno di tensione, l'effetto Miller su Cμ farà si che:
C μ '=C μ (1−K )≈325,5 pF
C μ ' '=C μ (1−
1
)≈1,8 pF
K
Come conseguenza si avrà:
19
Esercitazione n° 4: Amplificatore a doppio carico
ReqC μ= RS∥R F1∥r π ≈4,1 k Ω
τ Cμ ' ≈C μ '⋅R S∥r π≈1,33μ s
Quindi in questa configurazione il polo dominante in alta frequenza è
imposto dalla capacità Cμ', con una frequenza di taglio superiore di:
f
≈
H3dB
1
≈120 kHz
2 π τC '
μ
Osserviamo che a rigore il discorso asintotico in frequenza andrebbe
fatto rispetto alla costante di tempo associata alla capacità C E: infatti
per frequenze molto superiori alla frequenza associata a tale costante di
tempo, il circuito diviene un emettitore comune, mentre per frequenze
molto inferiori rispetto a tale frequenza il circuito è assimilabile ad un
doppio carico. Nel nostro caso la frequenza di taglio associata a C E si
trova a frequenze bassissime, infatti si può dimostrare che:
f CE ≈
1
1
2 π C E R E∥
gm
≈8,2 Hz
Possiamo, quindi, riassumere i risultati ottenuti nella seguente tabella:
Doppio Carico
Emettitore Comune
Av ≈ -4,1 V/V
Av ≈ -216 V/V
Rin ≈ 225 kΩ
Rin ≈ 8,3 kΩ
Rin ≈ 9,88 kΩ
Rin ≈ 9,88 kΩ
FL ≈ 0,66 Hz
FL ≈ 8,2 Hz
FH ⁓ 1,73 MHz
FH ≈ 120 kHz
Di seguito è riportata una simulazione SPICE per questa configurazione
che conferma le considerazioni fatte su guadagno di tensione e
frequenze di taglio.
20
Esercitazione n° 4: Amplificatore a doppio carico
Fig. 22: Diagramma di Bode ottenuto tramite simulazione SPICE con sw chiuso.
Si osservi che se la frequenza di taglio associata alla capacità CE fosse
stata scelta in modo tale da trovarsi a centro banda, sarebbe stato
possibile individuare sul diagramma di Bode entrambe le modalità di
funzionamento del circuito. Infatti se poniamo fCE = 2 kHz, otteniamo:
C E≈
1
≈1,95μ F
1
2π
f
g m CE
Fig. 23: Diagramma di Bode ottenuto tramite simulazione SPICE con CE = 1,95μF.
21
Esercitazione n° 4: Amplificatore a doppio carico
In una applicazione di tipo pratica, questa riconfigurazione del circuito
con il semplice inserimento del capacitore C E può essere immaginata
come un boost del guadagno dell'amplificatore. Ad esempio
immaginando ad una applicazione audio dove il segnale proviene da un
microfono, può tornare utile in alcune situazioni amplificare molto di più
il segnale a causa di un suo troppo basso livello. Ovviamente c'è un
prezzo da pagare per avere un maggiore guadagno di tensione. La
prima conseguenza è quella che la banda passante del sistema si
riduce come abbiamo potuto constatare dai calcoli precedenti. Sempre
considerando una applicazione audio è pure vero che nel secondo caso
la frequenza di taglio superiore è di 120 kHz che va molto al di la dei 22
kHz percepibili dall'orecchio umano. C'è un altro prezzo da pagare: il
rumore equivalente introdotto dal circuito.
Senza entrare nei dettagli, di seguito è riportato una simulazione SPICE
del confronto tra il rumore generato dallo stesso circuito nelle due
configurazioni. Come si vede il secondo caso è molto peggiorativo
rispetto al primo caso.
Fig. 24: Schematico in LTspice IV per la valutazione del rumore generato dal circuito
(nel primo caso la capacità CE è assente).
22
Esercitazione n° 4: Amplificatore a doppio carico
Fig. 25: Simulazione SPICE della densità spettrale di rumore generata
dall'amplificatore a doppio carico.
Fig. 26: Simulazione SPICE della densità spettrale di rumore generata
dall'amplificatore ad emettitore comune.
23
Esercitazione n° 4: Amplificatore a doppio carico
Appendice 1
Il teorema di Miller è un teorema sulle reti elettriche. Supponiamo di
considerare una impedenza posta tra due punti di una rete elettrica:
Fig. 27: Teorema di Miller.
Sia V1 e V2 il potenziale di questi due punti rispetto al potenziale
comune (GND). Si pone:
K=
V2
V1
Il teorema di Miller dice che è possibile una trasformazione che porta
dal circuito di Fig. 17.a a quello di Fig. 27.b scegliendo opportunamente
i valori delle impedenza Z1 e Z2. Ciò si dimostra facilmente imponendo
che il regime delle correnti nella rete elettrica resti inalterato, ovvero:
I Z1= I Z
I Z2 =I Z
Che si traduce nelle seguenti due condizioni:
V1 V1−V2 V1(1−K )
Z
=
=
← → Z1=
Z1
Z
Z
1−K
24
Esercitazione n° 4: Amplificatore a doppio carico
−V2 V1−V2 V2(1/ K −1)
Z
=
=
← → Z2=
Z2
Z
Z
1−1/ K
Quindi a patto di scegliere secondo le precedenti relazioni i valori di Z1
e Z2 le due reti possono essere considerate equivalenti. Ci sono in ogni
caso delle osservazioni da fare:
1)K non deve risentire dello spostamento dell'impedenza Z;
2)La trasformazione di Miller non si può utilizzare per il calcolo della
resistenza di uscita;
3)Se K è molto grande Z1 tende a zero, così come se K è molto piccolo
Z2 tende a zero.
25