Ezio Mazzola Appunti di Analisi Matematica
Ezio Mazzola
Page | 1
Ezio Mazzola Appunti di Analisi Matematica
Contents 1 ‐ Numeri .................................................................................................................................. 7 Numeri Periodici .................................................................................................................... 7 Numeri Irrazionali .................................................................................................................. 7 Proprietà del valore assoluto: ............................................................................................... 7 2 ‐ Successioni di numeri reali, limiti ......................................................................................... 8 Successione di numeri reali ................................................................................................... 8 Criterio di convergenza di Cauchy: .................................................................................... 8 Calcolo dei limiti .................................................................................................................... 8 Progressioni aritmetiche e geometriche ............................................................................... 8 Proprietà delle progressioni aritmetiche........................................................................... 9 Proprietà delle progressioni geometriche ......................................................................... 9 Media ponderata ................................................................................................................... 9 Media armonica ..................................................................................................................... 9 3 ‐ Elementi di analisi combinatoria ........................................................................................ 11 Permutazione di n oggetti distinti ....................................................................................... 11 Permutazione di n oggetti non distinti ................................................................................ 11 Disposizioni semplici ............................................................................................................ 11 Combinazioni semplici ......................................................................................................... 11 4 ‐ Funzioni .............................................................................................................................. 12 Funzioni esponenziali .......................................................................................................... 12 Proprietà delle funzioni esponenziali .............................................................................. 12 Funzioni logaritmiche .......................................................................................................... 12 Proprietà dei logaritmi .................................................................................................... 12 Funzioni iperboliche ............................................................................................................ 12 Proprietà delle funzioni iperboliche ................................................................................ 12 Funzioni parametriche ......................................................................................................... 14 Esempio ........................................................................................................................... 14 Funzioni trigonometriche circolari ...................................................................................... 14 Relazioni trigonometriche fra angoli che differiscono di π/2, π, 2k π ............................ 15 Formule di addizione ....................................................................................................... 15 Formule di duplicazione .................................................................................................. 16 Formule di triplicazione e di moltiplicazione................................................................... 16 Formule di bisezione ....................................................................................................... 16 Page | 2
Ezio Mazzola Appunti di Analisi Matematica
Formule parametriche ..................................................................................................... 16 Formule di prostaferesi ................................................................................................... 17 Formule di Werner .......................................................................................................... 17 Formule trigonometriche relative a triangoli e quadrilateri ........................................... 18 Tabella Relazioni tra funzioni trigonometriche ............................................................... 20 5 ‐ Geometria Analitica ............................................................................................................ 21 Coordinate rettilinee e coordinate piane ............................................................................ 21 Trasformazione di coordinate ............................................................................................. 21 Trasformazione da polari a cartesiane e viceversa ......................................................... 21 Trasformazioni fra coordinate cartesiane ....................................................................... 21 Retta .................................................................................................................................... 22 Circonferenza....................................................................................................................... 22 Ellisse ................................................................................................................................... 22 Iperbole ............................................................................................................................... 23 Parabola ............................................................................................................................... 23 Spirali Archimedea e Logaritmica ........................................................................................ 23 Spirale Archimedea ......................................................................................................... 23 Spirale Logaritmica .......................................................................................................... 24 Vettori Geometrici ............................................................................................................... 24 Vettori equivalenti ........................................................................................................... 24 Operazioni con Vettori .................................................................................................... 24 Vettori nello spazio .......................................................................................................... 25 6 ‐ Derivate e differenziali ....................................................................................................... 28 Derivata e differenziale di una funzione ............................................................................. 28 Derivata ........................................................................................................................... 28 7 ‐ Numeri complessi ............................................................................................................... 29 Proprietà: ............................................................................................................................. 29 Rappresentazione: ............................................................................................................... 29 Operazioni con numeri complessi ....................................................................................... 30 8 ‐ Calcolo letterale – Polinomi ............................................................................................... 31 Calcolo Letterale .................................................................................................................. 31 Regola di Ruffini ................................................................................................................... 31 Esempio: .......................................................................................................................... 31 Teorema fondamentale dell’algebra ................................................................................... 32 Page | 3
Ezio Mazzola Appunti di Analisi Matematica
Scomposizione di polinomi la cui espressione è una frazione razionale ............................. 32 Esempio ........................................................................................................................... 33 Equazioni algebriche ............................................................................................................ 33 Formule risolutive ............................................................................................................ 33 Relazioni tra i coefficienti e le radici di una equazione di secondo grado ...................... 34 9 ‐ Matrici, Determinanti, Sistemi di equazioni lineari ............................................................ 35 Matrici ................................................................................................................................. 35 Determinante di una matrice quadrata .............................................................................. 35 Proprietà dei determinanti .............................................................................................. 36 Sviluppo del determinante .............................................................................................. 36 Sistemi di equazioni lineari .................................................................................................. 36 Regola di Cramer per i sistemi di n equazioni lineari in n incognite ............................... 37 10 ‐ Integrali ............................................................................................................................ 38 Primitive e integrali indefiniti .............................................................................................. 38 Proprietà dell’integrale indefinito ................................................................................... 38 Integrali delle funzioni elementari .................................................................................. 38 Metodi di integrazione ........................................................................................................ 39 Metodo di sostituzione .................................................................................................... 39 Metodo di integrazione per parti .................................................................................... 39 Integrali definiti ................................................................................................................... 40 Proprietà degli integrali definiti....................................................................................... 40 Metodi di calcolo degli integrali definiti .......................................................................... 41 Metodi di Integrazione .................................................................................................... 41 Metodo di integrazione per parti .................................................................................... 42 Integrali Impropri ................................................................................................................ 42 Integrali con estremi infiniti ............................................................................................ 42 Integrale di una funzione discontinua ............................................................................. 42 11 ‐ Funzioni di più variabili ..................................................................................................... 43 Funzioni reali di più variabili reali ........................................................................................ 43 Derivate parziali, differenziale totale .................................................................................. 43 Incremento parziale ed incremento totale ..................................................................... 43 Derivate parziali ............................................................................................................... 43 Differenziale totale .......................................................................................................... 44 Derivata parziale e differenziale totale di una funzione composta .................................... 44 Page | 4
Ezio Mazzola Appunti di Analisi Matematica
Derivate parziale e differenziale totale di ordine superiore ............................................... 44 Derivate parziali ............................................................................................................... 44 Differenziale totale .......................................................................................................... 44 Superfici di livello ................................................................................................................ 44 Derivata secondo una direzione data, Gradiente ................................................................ 45 Derivata secondo una direzione data .............................................................................. 45 Gradiente ......................................................................................................................... 45 Legame tra gradiente e derivata secondo una direzione. ............................................... 45 Proprietà del gradiente ................................................................................................... 45 12 ‐ Integrali multipli, curvilinei, di superficie e operatore Hamiltoniano .............................. 47 Integrale doppio .................................................................................................................. 47 Proprietà .......................................................................................................................... 47 Integrale curvilineo .............................................................................................................. 47 Proprietà .......................................................................................................................... 48 Integrale di superficie .......................................................................................................... 48 Proprietà: ......................................................................................................................... 48 Divergenza, Rotore, Operatore Hamiltoniano .................................................................... 49 Divergenza di una funzione vettoriale ............................................................................. 49 Rotore di una funzione vettoriale ................................................................................... 49 Operatore Hamiltoniano ................................................................................................. 50 Formule di analisi vettoriale concernenti grad, rot div ................................................... 51 13 ‐ Equazioni differenziali e calcolo operazionale ................................................................. 52 Trasformata di Laplace ........................................................................................................ 52 Proprietà .......................................................................................................................... 52 Trasformate di Laplace ........................................................................................................ 53 Soluzione delle equazioni differenziali con il metodo operazionale ................................... 56 Esempio ........................................................................................................................... 57 14 – Serie ................................................................................................................................. 58 Serie Numeriche .................................................................................................................. 58 Proprietà .......................................................................................................................... 58 Criteri di convergenza della serie a termini positivi ........................................................ 59 Serie di funzioni ................................................................................................................... 59 Serie di potenze nel campo reale e complesso ............................................................... 59 Serie di Taylor e di Mac Laurin ........................................................................................ 59 Page | 5
Ezio Mazzola Appunti di Analisi Matematica
Sviluppi in serie di funzioni elementari sul campo reale ................................................. 60 Formule di Eulero ............................................................................................................ 61 Serie di Fourier .................................................................................................................... 61 Integrale di Fourier .............................................................................................................. 63 Page | 6
Ezio Mazzola Appunti di Analisi Matematica
1 - Numeri
Numeri Periodici
Il gruppo di cifre che si ripete all’infinito e’ detto periodo ( 0,3535... 0.35 ). Se le cifrasi
ripetono sempre, a partire dalla prima, il numero decimale si dice periodico semplice
( 0,3535... 0.35 ), se invece alcune cifre non si ripetono e’ detto periodico misto e le cifre
che non si ripetono sono dette antiperiodo ( 0,243535... 0.2435 )
I numeri periodici possono ricondursi a frazioni (frazione generatrice). La frazione generatrice
si trova come:
Numero periodico semplice: Al numeratore si mette il periodo e al denominatore tanti 9
quante sono le cifre del periodo ( 0.35 35 / 99 )
Numero periodico misto: Al numeratore si mette la cifra – l’antiperiodo e al denominatore
tanti 9 quante sono le cifre del periodo seguite da tanti 0 quante sono le cifre decimali
dell’antiperiodo.
0.142
142 1 141
;
990
990
2.15
215 2 213
;
99
99
8.534
8534 85 8449
990
990
Numeri Irrazionali
I numeri decimali illimitati non periodici rappresentano i numeri reali irrazionali
2 1.414213561...
Per i numeri reali si definisce il modulo o valore assoluto |x|
Proprietà del valore assoluto:
1) x x
2)
x y x y
3)
x y x y
4)
xy x y
5)
x
x
y
y
con
x y
Page | 7
Ezio Mazzola Appunti di Analisi Matematica
2 - Successioni di numeri reali, limiti
Successione di numeri reali
L’insieme dei numeri 1, 2, 3, 4, …., n, …. Si dice successione degli interi naturali.
Un insieme di elementi è numerabile quando esiste una legge che lo pone in corrispondenza
biunivoca con la classe degli interi naturali.
Si dice successione un insieme di elementi che e’ posto in corrispondenza biunivoca con la
successione degli interi naturali e si indica con:
xn oppure x1 , x2 ,....., xn ,.....
Una successione e’:
1. Limitata superiormente quando
k tale che x n k n
h tale che x n h n
3. Limitata quando k e h tale che h x n k n
2. Limitata inferiormente quando
La successione {xn} è convergente al limite finito a quando, fissato un numero ε > 0 ,piccolo a
piacere, è possibile determinare un indive v(ε) tale che per ogni n ≥ v si abbia | xn – a | < ε
lim x
n
n
a oppure
x n a
per
n
Criterio di convergenza di Cauchy: Condizione necessaria e sufficiente affinché la successione {xn} sia convergente è che ad
ogni ε > 0 e’ possibile associare un intero v = v(ε), tale che per ogni coppia di indici m e n, con
m ≥ v e n ≥ v , si abbia | xm- xn | < ε.
Calcolo dei limiti
Una successione che converge a 0 è detta successione infinitesima e si indica come:
xn 0
per n
Criteri sufficienti per stabilire se una successione è infinitesima:
1. Criterio del confronto: date {xn} e {yn}, con {yn} convergente a 0 per n → , se
|xn| ≤ !yn| allora {xn} → 0
2. Criterio della radice: data {xn}, se esiste un numero 0 < α < 1 tale che
lim x
n
1n
n
allora
x n 0
3. Criterio del rapporto: data {xn}, se esiste un numero 0 < α < 1 tale che
lim
n
x n 1
xn
allora
xn 0
Criteri analoghi a quelli esposti per le successioni infinitesime sono validi anche per le
successioni divergenti, se consideriamo che
x n equivale a
1
0
xn
Progressioni aritmetiche e geometriche
Si definisce progressione aritmetica (o progressione per differenza) una successione nel
quale e’ costante la differenza d, detta ragione, tra un termine e quello che lo precede:
Page | 8
Ezio Mazzola Appunti di Analisi Matematica
xn+1 – xn = d
Si definisce progressione geometrica (o progressione per quoziente) una successione nel
quale e’ costante il rapporto q, detto ragione, tra un termine e quello che lo precede:
xn+1 / xn = q
Proprietà delle progressioni aritmetiche 1. noti x1 e d : xn = x1 + ( n -1 ) d
2. noti xm , d ed n : xm+n = xm + nd
3. noti xm , xp ed n, con xp > xm , per inserire n termini tra xm ed xp , la ragione d è data
da: d
x p xm
n 1
4. La media aritmetica m di n termini è: m
x1 x 2 .... x n
n
5. Data la progressione x1 , x2 , …, xn-2 , xn-1 , xn la somma degli estremi x1 + xn è uguale
alla somma dei termini equidistanti dagli estremi: x2 + xn-1 , x3 + xn-2 , ……
x1 x n
n
2
6. La somma Sn di n termini consecutivi è: S n
Proprietà delle progressioni geometriche 1. noti x1 e q : xn = x1 qn -1
n
2. noti xm , q ed n : xm+n = xm q
3. noti xm , xp ed n, con xp > xm , per inserire n termini tra xm ed xp , la ragione q è data
da:
q n 1
xp
xm
4. La media geometrica m g di n termini è:
m g n x1 x 2 ...x n
5. Data la progressione x1 , x2 , …, xn-2 , xn-1 , xn il prodottodegli estremi x1 xn è uguale al
prodotto dei termini equidistanti dagli estremi: x2 xn-1 , x3 xn-2 , ……
6. Il prodotto Pn di n termini consecutivi è: Pn
x1 x n
7. La somma Sn di n termini consecutivi è: S n x1
lim S n
n
n
qn 1
q 1
x1
per q 1
q 1
Media ponderata
Dati n numeri x1 , x2 ,…., xn , si dice media ponderata, m p , degli n numeri xi ai quali sono
attribuiti i pesi yi il rapporto:
mp
x1 y1 x 2 y 2 ..... x n y n
n
Media armonica
Dati n numeri x1 , x2 ,…., xn , si dice media armonica, m a , il rapporto:
ma
n
1
1
1
....
x1 x 2
xn
Page | 9
Ezio Mazzola Appunti di Analisi Matematica
Dati due numeri x1 , x2 , le relazioni tra media aritmetica m , geometrica
m g e media
armonica m a dei due numeri è:
m g m ma
con m m g ma
Page | 10
APPUNTI DI ANALISI MATEMATICA
3 - Elementi di analisi combinatoria
Permutazione di n oggetti distinti
Dati n oggetti diversi collocati in n posti numerati da 1 a n, si definisce permutazione
semplice degli n oggetti ogni diverso collocamento degli n oggetti negli n posti numerati. Il
numero totale di permutazioni Pn è:
Pn 1 2 3....n n! per definizione 1! 1 0! 1
Permutazione di n oggetti non distinti
k oggetti uguali tra loro e n-k uguali tra loro ma distinti dai precedenti. Il numero di tali
permutazioni è dato da:
n!
k!n k !
Questo è detto coefficiente binomiale e si indica come:
n
n!
k k!n k !
0
per definizione 1
0
Disposizioni semplici
Si definiscono disposizioni semplici di n oggetti distinti a k a k o di classe k (n≥k) tutti i
possibili gruppi ordinati di k oggetti presi tra gli n dati. Due disposizioni sono distinte se
differiscono o per l’ordine con cui sono disposti gli oggetti o per gli oggetti contenuti. Il numero
delle disposizioni semplici si denota con Dnk ed è:
Dnk nn 1n 2 ....n k 1
Combinazioni semplici
Si definiscono combinazioni semplici di n oggetti distinti in classe k, ogni possibile gruppo di k
oggetti comunque presi tra gli n oggetti dati. Due combinazioni sono distinte se differiscono
almeno per un oggetto contenuto. Il numero delle combinazioni semplici si denota con Cnk ed
è:
C nk
11
nn 1n 2 ....n k 1 n
k!
k
APPUNTI DI ANALISI MATEMATICA
4 - Funzioni
Funzioni esponenziali
Siamo a>0 costante e x variabile reale; la potenza y = ax si dice funzione esponenziale di
base a.
Proprietà delle funzioni esponenziali 1.
2.
3.
4.
5.
a0 = 1
1x = 1 per ogni x
x x
x+x
a a =a
x x
a b = (a b)x
(ax )y = ax y
Funzioni logaritmiche
Si definiste funzione logaritmica di base a la funzione: y = loga (x)
Proprietà dei logaritmi 1. loga 1 = 0 per ogni a
2. loga b = 1 / logb a
3. logb m = (loga m) (1 / logb a ) Cambiamento di base
Funzioni iperboliche
Combinazioni di funzioni esponenziali vengono considerate come nuove funzioni dette
funzioni iperboliche.
Proprietà delle funzioni iperboliche 1. Ch2 x – Sh2 x = 1
2. Ch (x+y) = Ch x Ch y + Sh x Sh y
3. Sh (x+y) = Sh x Ch y + Ch x Sh y
4.
12
Th( x y )
th x th y
1 th x th y
APPUNTI DI ANALISI MATEMATICA
Funzioni iperboliche
Denominazione
Seno Iperbolico
Equazione
sh x
e x ex
2
Coseno Iperbolico
e x ex
ch x
2
Tangente Iperbolica
sh x e x e x
th x
ch x e x e x
Cotangente Iperbolica
13
ch x e x e x
cth x
sh x e x e x
Grafico
Funzione inversa
Grafico
arsh x ln x x 2 1
arch x ln x x 2 1 ln x x 2 1
con x 1
1 1 x
ln
2 1 x
x 1
arth x
con
1 1 x
ln
2 1 x
x 1
arcth x
con
APPUNTI DI ANALISI MATEMATICA
Funzioni parametriche
Siano x ed y le coordinate di un punto P del piano espresse dalle equazioni:
x t
y t
con T1 ≤ t ≤ T2
Quando t varia tra T1 ≤ t ≤ T2 il punto P descrive sul piano un curva. Le equazioni di cui sopra
si dicono equazioni parametriche della curva descritta da P e t si dice parametro.
Esempio Si consideri la funzione x2 – y2 = 1 il cui diagramma è un’iperbole
equilatera.
Posto x = ch t e y = sh t, si ha l’equazione parametrica
dell’iperbole : ch2 t – sh2 t = 1. Il parametro t dell’equazioni
parametriche in esame è numericamente uguale al doppio della
superficie del settore iperbolico OAP
Si consideri la funzione x2 + y2 = 1 il cui diagramma è una
circonferenza.
Posto x = cos t e y = sin t, si ha l’equazione parametrica della
circonferenza : cos2 t + sin2 t = 1. Il parametro t dell’equazioni
parametriche in esame è numericamente uguale al doppio della
superficie del settore circolare OAP
Funzioni trigonometriche circolari
Le funzioni trigonometriche stabiliscono una corrispondenza tra l’insieme degli angoli Φ e
l’insieme R dei numeri reali.
Si definisce radiante l’angolo piano al centro che su
una circonferenza intercetta un arco la cui
lunghezza è uguale a quella del raggio a cui
appartiene:
1 rad = 57°17’44,806” 1° = 0,017453293 rad
Le funzioni trigonometriche sono riportate nele figure
successive:
OC / OP cos( ) OS / OP sec( ) 1
cos( )
CP / OP sin( ) OH / OP cos ec( ) 1
sin( )
AT / OP tg ( ) BD / OP ctg ( ) 1
tg ( )
14
APPUNTI DI ANALISI MATEMATICA
Relazioni trigonometriche fra angoli che differiscono di π/2, π, 2k π
sin( ) sin( ) cos
2
cos( ) cos( ) sin
2
sin( ) sin( 2k ) cos( ) sin( 2k ) tg ( ) tg ( k ) cot g ( ) cot g ( k )
tg ( ) tg ( ) ctg
2
cot g ( ) cot g ( ) tg
2
Relazioni fondamentali tra funzioni dello stesso arco
sin 2 ( ) cos 2 ( ) 1
sin( )
tg ( )
cos( )
cos( )
ctg ( )
sin( )
Formule di addizione sin( ) sin( ) cos( ) cos( ) sin( )
cos( ) cos( ) cos( ) sin( ) sin( )
tg ( ) tg ( )
tg
1 tg ( ) tg ( )
cot g ( ) cot g ( ) 1
cot g
cot g ( ) cot g ( )
15
APPUNTI DI ANALISI MATEMATICA
Formule di duplicazione sin( 2 ) 2 sin( ) cos( )
cos(2 ) cos 2 ( ) sin 2 ( ) 1 2 sin 2 ( ) 2 cos 2 ( ) 1
2tg ( )
tg (2 )
1 tg 2 ( )
cot g 2 ( ) 1
cot g (2 )
2 cot g ( )
Formule di triplicazione e di moltiplicazione sin(3 ) 3 sin( ) 4 sin 3 ( )
cos(3 ) 4 cos 3 ( ) 3 cos( )
tg (3 )
3tg ( ) tg 3 ( )
1 3tg 2 ( )
cot g 3 ( ) 3 cot g ( )
3 cot g 2 ( ) 1
sin( n ) sin (n 1) cos( ) cos(n 1) sin( )
cos(n ) cos(n 1) cos( ) sin (n 1) sin( )
tg (n 1) tg ( )
tg (n )
1 tg (n 1) tg ( )
cot g (3 )
Formule di bisezione 1 cos( )
1
sin
2
2
1 cos( )
1
cos
2
2
1 cos( )
sin( )
1 cos( )
1
tg
1 cos( ) 1 cos( )
sin( )
2
2
1 1 1 tg ( )
tg
tg ( )
2
Formule parametriche 2t
sin( )
t tg
2
2
16
1 t
cos( )
1 t2
1 t2
tg ( )
2t
1 t2
APPUNTI DI ANALISI MATEMATICA
Formule di prostaferesi 1
1
sin( p ) sin( q ) 2 sin ( p q ) cos ( p q )
2
2
1
1
sin( p ) sin( q ) 2 cos ( p q ) sin ( p q )
2
2
1
1
cos( p ) cos(q ) 2 cos ( p q ) cos ( p q )
2
2
1
1
cos( p ) cos(q ) 2 sin ( p q ) sin ( p q )
2
2
( p q)
( p q)
sin( p ) cos(q) 2 sin
45 cos
45
2
2
( p q)
( p q)
sin( p ) cos(q ) 2 sin
45 cos
45
2
2
1
tg ( p q )
sin( p ) sin( q )
2
sin( p ) sin( q )
1
tg ( p q)
2
sin( p ) sin( q )
1
tg ( p q )
cos( p ) cos(q )
2
sin( p q )
tg ( p ) tg (q )
cos( p ) cos(q )
sin( p q )
cot g ( p ) cot g (q)
sin( p ) sin( q )
Formule di Werner 1
cos( ) cos( )
2
1
cos( ) cos( ) cos( ) cos( )
2
1
sin( ) cos( ) sin( ) sin( )
2
1
cos( ) sin( ) sin( ) sin( )
2
sin( ) sin( )
17
APPUNTI DI ANALISI MATEMATICA
Formule trigonometriche relative a triangoli e quadrilateri Triangolo rettangolo: a c sin( ) c cos( ) b tg ( ) b cot g ( )
a
a
b c cos( ) c sin( )
tg ( ) cot g ( )
Fig: 1
Triangolo qualsiasi – Teorema dei seni a
b
c
2R
sin( ) sin( ) sin( )
Fig: 2
Teorema delle proiezioni (Fig: 3)
a b cos( ) c cos( )
b c cos( ) a cos( )
c a cos( ) b cos( )
Teorema del coseno (Fig: 3)
a 2 b 2 c 2 2bc cos( )
b 2 a 2 c 2 2ac cos( )
c 2 a 2 b 2 2ab cos( )
Formula delle Tangenti (Fig: 3)
1
1
tg ( )
cot g
ab
2
2
ab
1
1
tg ( ) tg ( )
2
2
Fig: 3
Formule di Briggs (Fig: 3)
sin
2
( p b)( p c)
bc
cos
2
p( p a)
bc
tg
2
Con p semiperimetro. Formule analoghe per gli angoli β/2 e γ/2.
18
( p b)( p c)
p( p a)
APPUNTI DI ANALISI MATEMATICA
Formule di Delambre
cos
ab
c
cos
(Fig: 3)
2
2
Formule analoghe per gli angoli β/2 e γ/2.
Formule per la determinazione dell’area S di un triangolo qualsiasi (Fig:
4)
1
ab sin( )
2
S p ( p a )( p b)( p c)
S
1 1 1
S p 2 tg tg tg
2 2 2
a 2 sin( ) sin( )
S
2 sin( )
S 2 R 2 sin( ) sin( ) sin( )
Fig: 4
Con R raggio del cerchio circoscritto e p semiperimetro.
Formule per calcolo altezze, mediane e bisettrici di un triangolo (Fig: 5)
Altezze ha , hb , hc
ha
2
a
p( p a )( p b)( p c)
Bisettrici ba , bb , bc
2
bcp( p a )
bc
ba
Mediane ma , mb , mc
ma
Fig: 5
1
2b 2 2c 2 a 2 )
2
Parallelogramma (Fig: 6)
S ab sin( )
Fig: 6
Quadrilatero (Fig: 7)
S
1 1
dd sin( )
2
Fig: 7
19
APPUNTI DI ANALISI MATEMATICA
Tabella Relazioni tra funzioni trigonometriche sin( )
sin( )
cos( )
tg ( )
cot g ( )
sec( )
cos ec( )
20
cos( )
1 cos 2 ( )
1 sin 2 ( )
sin( )
1 sin ( )
2
1 sin 2 ( )
sin( )
1
1 sin 2 ( )
1
sin( )
tg ( )
cot g ( )
tg ( )
1
1 tg ( )
1 cot g ( )
1
cot g ( )
2
1 tg ( )
2
1 cos 2 ( )
cos( )
cos( )
2
1
cot g ( )
sec2 ( ) 1
1
1
cos( )
1 tg 2 ( )
1 cot g 2 ( )
cot g ( )
1 tg 2 ( )
tg ( )
1 cot g 2 ( )
1 cos ( )
2
1
sec 2 ( )
1 cot g ( )
1 cos ( )
1
1
1
sec( )
2
1
tg ( )
2
sec( )
sec ( ) 1
2
cos ec( )
1
cos ec( )
1
1
cos ec 2 ( )
1
cos ec 2 ( ) 1
cos ec 2 ( ) 1
cos ec( )
cos ec 2 ( ) 1
sec( )
sec2 ( ) 1
APPUNTI DI ANALISI MATEMATICA
5 - Geometria Analitica
Coordinate rettilinee e coordinate piane
Abbiamo coordinate piane cartesiane o coordinate polari (vedi figura)
Trasformazione di coordinate
Trasformazione da polari a cartesiane e viceversa x cos( )
y sin( )
x2 y 2
arctg
y
x
Trasformazioni fra coordinate cartesiane Traslazione (Fig: 1 A)
x x1 a
y y1 b
Rotazione (Fig: 1 B)
x x1 cos( ) y1 sin( )
x1 x cos( ) y sin( )
y x1 sin( ) y1 cos( )
y1 x sin( ) y cos( )
Rototraslazione (Fig: 1 C)
x x1 cos( ) y1 sin( ) a
x1 x a cos( ) y b sin( )
y x1 sin( ) y1 cos( ) b
y1 y b cos( ) x a sin( )
b
a
Fig: 1
APPUNTI DI ANALISI MATEMATICA
Retta
L’equazione generale di una retta è ax+by+c=0 oppure in forma canonica y=mx+q.
Prendendo in considerazione l’equazione canonica m rappresenta la tangente dell’angolo α.
Dati due punti, P1 (x1, y1) e P2 (x2, y2), la retta da essi individuata ha equazione:
y
y2 y1
y y1
x y1 2
x1
x2 x1
x2 x1
Date due rette:
y m1 x q1
y m2 x q2
Le rette sono tra loro parallele se m1=m2 , sono perpendicolari se m1 m2 =-1. In generale per
l’angolo φ formato da due rette si ha:
tg ( )
m2 m1
1 m2 m1
Dati 3 punti P1 (x1, y1) , P2 (x2, y2) e P3 (x3, y3) , vertici di un triangolo, l’area S del triangolo è:
S
1 x1 x3
2 x2 x3
y1 y3
y2 y3
1
x1 x3 y2 y3 x2 x3 y1 y3
2
Circonferenza
L’equazione di una circonferenza di centro C(a,b) e raggio r è:
x 2 y 2 2ax 2bx a 2 b 2 r 2 0
Ellisse
Luogo geometrico dei punti tali che risulti costante
la somma delle distanze dai fuochi.
x2 y2
2 1 con b 2 a 2 c 2
2
a
b
Si definisce eccentricità dell’ellisse il rapporto:
e
22
c
a
a 2 b2
a
APPUNTI DI ANALISI MATEMATICA
Iperbole
Si definisce come il luogo geometrico dei punti
tali che risulta costante il valore assoluto della
differenza delle distanze dai fuochi:
x2
y2
1 con a 2 c 2 0
a2 a2 c2
Ponendo b2=c2-a2 si ha l’equazione canonica
dell’iperbole:
x2 y2
1
a2 b2
Le rette di equazione:
y
b
x e
a
y
b
x
a
Sono dette asintoti dell’iperbole. Se l’asse reale è uguale all’asse immaginario (a=b) l’iperbole
si dice equilatera ed ha equazione x2-y2 = a2.
Parabola
Luogo geometrico dei punti equidistanti da un
punto detto fuoco e da una retta detta direttrice..
L’equazione canonica della parabola è:
y
1 2
x
2p
y ax 2 bx c rappresenta l’equazione
generale della parabola. Se a>0 la parabola ha
la concavità verso l’alto, mentre se a<0 la
concavità è verso il basso.
Spirali Archimedea e Logaritmica
Spirale Archimedea Si consideri un punto P che si muove di moto rettilineo uniforme sulla retta OV la quale
compie un moto di rotazione uniforme attorno ad O. La spirale ha equazione:
23
APPUNTI DI ANALISI MATEMATICA
a
a
Rotazione antioraria
Rotazione oraria
Il passo della spirale è 2πa.
Spirale Logaritmica Ha equazione
a e m
Con a costante positive e m costante arbitraria.
Vettori Geometrici
Una grandezza vettoriale è definita da modulo, direzione e verso.
Vettori equivalenti hanno lo stesso modulo, la stessa direzione e verso
Operazioni con Vettori Somma Dati due vettori v1 e v2 , il vettore somma v3 si ottiene come da
figura. Proprietà:
v1 + v2 = v2 + v1
commutativa
v1 + v2 + v3 = (v1 + v2 ) + v3
associativa
Differenza Si definisce differenza di due vettori v1 - v2 il vettore v3 che aggiunto a v2 dà v1
Moltiplicazione e divisione di un vettore per un numero Moltiplicare un vettore v per un numero x significa costruire un nuovo vettore, xv ,il cui
modulo è moltiplicato per x. Il vettore xv ha lo stesso verso o verso opposto a seconda che
sia x>0 o x<0. Dividere il vettore v per un numero x≠ 0, significa trovare il vettore v/x che
moltiplicato per x dia v
24
APPUNTI DI ANALISI MATEMATICA
Prodotto scalare di due vettori Fig: 1
Con riferimento alla figura 1a si definisce proiezione algebrica di v o coordinata di v sull’asse
0X il vettore Pr0x v.
Con riferimento alla figura 1b si definisce proiezione algebrica di v o coordinata di v sull’asse
0X la lunghezza (scalare, |v’| ) del vettore v presa con segno + o – secondo che il vettore v
abbia o no lo stesso verso dell’asse OX.
Il prodotto scalare di due vettori v1 e v2 (v1 v2) è uguale al
prodotto fra il modulo di uno dei vettori per la proiezione
algebrica dell’altro vettore nella direzione del primo.
v1 v 2 v1 v 2 cos( )
Proprietà:
v1 v 2 v 2 v1
commutativa
v1 v 2 v v1 v v 2 v
xv1 v 2 xv1 v2
vv v
associativa
2
Vettori nello spazio Fig: 2
Dati tre assi perpendicolari tra loro (Fig: 2) ed il segmento MN come unit’ di misura dei tre
assi abbiamo un sistema di coordinate spaziali. I vettori di modulo unitario (MN) i, ,j e k sono
anche detti versori. Fig. 2a sistema destrorso, Fig 2b sistema sinistrorso. Si definiscono
coordinate del vettore v le proiezioni algebriche di v sugli assi (Fig: 2c). Ogni vettore è uguale
alla somma dei tre vettori basi moltiplicati per le coordinate di v:
v xi yj zk
e il suo mod ulo è :
v x2 y2 z2
Dati due vettori v1(x1, y1, z1) e v2(x2, y2, z2) il loro prodotto scalare è:
v1 v 2 x1 x 2 y1 y 2 z1 z 2
Dati due vettori v1(x1, y1, z1) e v2(x2, y2, z2), essi sono perpendicolari se il loro prodotto scalare
è nullo:
v1 v 2 x1 x 2 y1 y 2 z1 z 2 0
APPUNTI DI ANALISI MATEMATICA
Se si proietta geometricamente un vettore v sugli assi, i vettori ottenuti sono detti componenti
di v e sono tali che:
v Pr0 x v Pr0 y v Pr0 z v
Con riferimento alla figura gli angoli α , β e γ formati dai semiassi
positivi con il vettore v sono determinati dalle relazioni:
cos( )
x
v
cos( )
y
v
cos( )
z
v
Se |v|=1 si ha
cos 2 ( ) cos 2 ( ) cos 2 ( ) 1
Dati due vettori v1(x1, y1, z1) e v2(x2, y2, z2) l’angolo φ che essi
formano è determinato da:
cos( )
v1 v 2
v1 v 2
Prodotto vettoriale Si definisce prodotto vettoriale di un vettore v1 con un vettore v2 un terzo vettore v3 , e si
indica v3 = v1 ^ v2 (a volte anche con v3 = v1 x v2) ottenuto nel seguente modo:
il modulo di v3 è uguale all’area del parallelogramma OABD,
data da | v1|.| v2|sin(φ), la direzione di v3 è perpendicolare al
piano del parallelogramma mentre il verso è tale che la terna
v1 v2 v3 sia destrorsa.
Proprietà:
v1 v 2 0 se v1 e v 2 sono sulla stessa retta
v1 v 2 v 2 v1 prodotto vettoriale non è commutativo
v1 v 2 v3 v v1 v v2 v v3 v Pr oprietà distributiva
mv1 v 2 m v1 v 2
v1 v 2 v1 v 2 2 v1 v 2 2 v 2 v1
Prodotti vettoriali dei vettori base (versori):
ii 0 i j k ik j
j i k
j j0
j k i k i j k j i k k 0
Dati due vettori v1(x1, y1, z1) e v2(x2, y2, z2) il loro prodotto vettoriale in funzione delle
coordinate dei vettori è espresso in forma matriciale dalla:
y1
y
2
z1
z1
x1
x1
z2
z2
x2
x2
y1
v1 v 2
y 2
Mentre il prodotto in funzione delle componenti i , j e k è dato dalla:
i
x1
j
y1
k
z1 v1 v 2
x2
y2
z2
Prodotto misto Si definisce prodotto misto di tre vettori v1 v2 e v3 , presi nell’ordine indicato il prodotto scalare
di v1 per il prodotto vettoriale v2 ^ v3; è v1. (v2 ^ v3) = ( v1 ^ v2 ) . v3 e si indica come (v1, v2, v3)
Proprietà: (v1, v2, v3) è uguale al volume del parallelepipedo costruito sui vettori v1, v2, v3 . Il
volume è positivo se v1, v2, v3 è una terna sinistrorsa, negativo al contrario.
26
APPUNTI DI ANALISI MATEMATICA
v1 , v2 , v3 v2 , v3 , v1 v3 , v1 , v2 v2 , v1 , v3 v3 , v2 , v1 v1 , v3 , v2
v1 v2 , v3 , v4 v1 , v3 , v4 v2 , v3 , v4
mv1 , v2 , v3 mv1 , v2 , v3
v1 , v1 , v 2 0
Il prodotto misto, in funzione delle coordinate dei vettori, si esprime in forma matriciale come.
27
x1
y1
z1
x2
y2
z 2 v1 , v 2 , v3
x3
y3
z3
APPUNTI DI ANALISI MATEMATICA
6 - Derivate e differenziali
Derivata e differenziale di una funzione
Derivata Sia y=f(x) una funzione reale definita nell’intervallo I ; si definisce incremento della variabile
indipendente x nel passaggio dal punto iniziale x 0 I al punto x= x0+h la differenza
Δx=x-x0=h. La funzione si incrementa corrispondentemente di Δy= f(x0+h)-f(x0). Si definisce
rapporto incrementale la quantità:
y f ( x 0 h ) f ( x 0 )
x
h
Il rapporto incrementale rappresenta la pendenza media della funzione f(x) nell’intervallo x0;
x0+h. Si definisce derivata il limite (se esiste) del rapporto incrementale per h tendente a 0:
lim
h0
f ( x 0 h) f ( x 0 )
f ' ( x0 )
h
La derivata f ‘(x0) rappresenta il coefficiente angolare della retta tangente alla funzione nel
punto P di coordinate [x0 ; f(x0)]. Se nel punto x0 la funzione f(x0) ammette derivata finita,
allora f(x0) è continua in x0.
28
APPUNTI DI ANALISI MATEMATICA
7 - Numeri complessi
Il campo dei numeri complessi può essere inteso come un ampliamento del campo dei
numeri reali e permette di determinare per ogni equazione algebrica di grado n, Pn(x)=0,
n radici.
Proprietà:
Posto α =(a,b) e β = (c,d) si ha:
uguaglianza α = β se a=c e b=d
addizione α + β = γ con γ = (a+c , b+d) ; valgono le proprietà commutativa ed
associativa
moltiplicazione α β = γ con γ = (ac-bd , ad+bc) ; valgono le proprietà commutativa,
associativa e distributiva
sottrazione α - β = γ con γ = (a-c , b-d)
divisione α / β = γ con
ac bd ad bc
, 2
2
2
2
a b a b
Rappresentazione:
Forma Algebrica: a
Forma Trigonometrica:
jb
cos( ) j sin( )
con
a b
2
2
a
cos( )
a b
b
arctg 2k
a
sin( )
b
a b2
2
con a 2 b 2
e e j cos( ) j sin( )
con a 2 b 2
b
e arg( ) arctg
a
Forma Polare:
Il complesso coniugato di
29
2
Forma Esponenziale:
e j
2
a jb si indica con
ed equivale a
a jb
APPUNTI DI ANALISI MATEMATICA
Operazioni con numeri complessi
Operazioni
Forma più conveniente da utilizzare
Trigonometrica
Esponenziale
Algebrica
a c j b d
e j
1
j
e
/
1
cos(n1 ) j sin(n1 )
n
cos(n1 ) j sin(n1 )
n
n
n
ln( )
n
ln j 1 2k
1 2k
2k
j sin 1
n
n
cos
n
n
n
n
; 1 2
n
; n1
1
e
e
j
jn1
1 2 k
n
Note
; 1 2
e jn
(*) Nella forma polare sono riportate le operazioni con cui si calcolano le coordinate polari
30
2
2
Polare(*)
n
n
; n1
;
1 2k
n
n intero positivo
n intero positivo
n valori (per k=0,1,2...n-1)
infiniti valori (per k=0,1,2...)
APPUNTI DI ANALISI MATEMATICA
8 - Calcolo letterale – Polinomi
Calcolo Letterale
n
n
a b n a nk b k
k 0 k
n
n
a b n 1k a nk b k
k 0
k
Binomio di Newton
(a b)(a b) a 2 b 2
a b a n1 a n2 b a n3b 2 ..... ab n2 b n1 a n b n
a b a
a b a
n 1
n2
n 3
n2
n 1
a b a b ..... ab b
n 1
a n 2 b a n 3b 2 ..... ab n 2 b n 1
a b
2
a a2 b
a a2 b
2
2
Si consideri il polinomio P ( x ) a 0 x a1 x
n
n 1
a
a
bn
bn
n
n
n pari
n dispari
Formula dei radicali doppi
a 2 x n 2 ... a n 1 x a n ordinato secondo
la variabile x, con n intero e coefficienti reali o complessi. Si dice radice di P(x) il valore della
variabile x per cui P(x)=0. Un polinomio può essere diviso per (x-b) ottenendo un resto P(b).
Se però b è una radice P(b)=0.
P( x) ( x b) P1 ( x) con P1 ( x) polinomio di grado n 1
Regola di Ruffini
Dividendo il polinomio P(x) per il binomio (x-b) si ottiene:
P ( x ) ( x b) Q ( x ) R
Con
Q ( x) a 0 x n 1 a 0 b a1 x n 2 a 0 b 2 a1b a 2 x n 3 ....
R a 0 b a1b
n
n 1
... a n 1b a n P (b)
I coefficienti indicati sono ottenuti mediante la regola di Ruffini
a0
b
a1
a0 b
a0
a2
an
a b
a0 b a1 b
n 1
0
a1 a 0 b a 2 a 0 b 2 a1b
a n a 0 b n a1b n 1 ... a n 1b
Esempio: P( x) x 4 3x 2 7 x 8 ;
xb x3
1
3
1
Q ( x) x 3 3 x 2 12 x 29 ;
0 3 -7
3 9 36
3 12 29
R 95
a1b n 2 ... a n 1 b
8
87
95
APPUNTI DI ANALISI MATEMATICA
Teorema fondamentale dell’algebra
Ogni polinomio P(x) di grado n nel campo complesso possiede n radici tali che, indicando con
b1,b2,…,bn le n radici del polinomio, si ha:
P ( x) a 0 x b1 1 x b2 2 .... x bn n
k
k
k
Con k1,k2,…,kn≥1 interi. L’espressione:
x bi k
i
1 i n
Indica che la radice i-esima è multipla di ordine ki, ciò pone in evidenza che P(x) è divisibile
per x bi i , mentre non è divisibile per x bi
k
ki 1
Scomposizione di polinomi la cui espressione è una frazione razionale
Si consideri il polinomio
P ( x ) a 0 x b1 1 x b2 2 ....x bm m
k
k
k
Espresso mediante fattori, con k1+k2+…km=n; se b1 è una radice multipla di ordine k1>1 di
P(x), allora è anche radice multipla di ordine k1-1 della derivata P’(x).
Se (a+jb) è radice di P(x) a coefficienti reali, allora anche (a-jb) è radice di P(x) e a ciascuna
coppia di radici complesse coniugate corrisponde un’espressione di tipo
x 2 cx d ; se le
radici complesse e coniugate sono multiple di ordine μ l’espressione sara’ x cx d
2
Si consideri il polinomio F(x)/f(x); se
f ( x) x a x b ....x 2 cx d
Con x cx d a radici complesse e coniugate (p-jq e p+jq), con α>1 e β>1 interi, allora
F(x)/f(x) può essere scomposto come:
2
A0,
A1, 1
Ak , k
A 1,1
F ( x)
B
...
...
...
1
k
x a x b
f ( x) x a
x a
x a
C 0,
C1, 1
C * 0,
C *1, 1
...
x p jq x p jq x p jq 1 x p jq 1
C 1,1
C * 1,1
x p jq x p jq
Con A0; A1,α-1;…; B; C0,β;… coefficienti reali e complessi. I coefficienti A; B; C sono ottenuti
mediante le relazioni:
Ak , k
1 dk
F ( x)
k x a
k! dx
f ( x) x a
F ( x)
per k 0 è : A0, x a
f ( x) x a
F ( x)
B x b
f ( x ) x b
C k , k
1 dk
F ( x)
k x p jq
k! dx
f ( x) x p jq
C * k , k
è il complesso coniugato di C k , k
32
F ( x)
per k 0 è : C 0, x p jq
f ( x) x p jq
APPUNTI DI ANALISI MATEMATICA
Esempio:
Scomposizione di
F ( x)
x2 2
4
f ( x) x x 3 3 x 2 5 x 2
P ( x)
Si scompone in fattori P(x):
P( x)
x2 2
x 2 x 1
3
A0,3
x 1
3
A1, 2
x 1
2
A2,1
B
x 1 x 1
x2 2
x2 2
3
3
A0,3 x 1
1
3
x 2 x 1 x1 x 2 x 1 3
d
x 2 4x 2
1
x2 2
3
A1, 2 x 1
3
2
x 2 x 1 x1 x 2 x 1 3
dx
A2,1
1 d 2
1 12
2
x2 2
3
1
x
2
3
3
2 dx
x 2 x 1 x1 2 x 2 x1 9
2
x2 2
B x 2
3
x 2 x 1 x 2 9
Per cui:
P( x)
1
x 1
3
1
3 x 1
2
2
2
9x 1 9 x 1
Equazioni algebriche
Si dice equazione algebrica di grado n un’equazione nella forma P(x)=0, dove P(x) è un
polinomio di grado n.
Formule risolutive Equazioni di primo grado ax b 0
x
b
a
Equazioni di secondo grado ax 2 bx c 0
Le soluzioni sono:
x
b b 2 4ac
2a
b 2 4ac è detto discriminante.
1. Δ>0 due radici reali e distinte
2. Δ=0 due radici reali e coincidenti
3. Δ<0 due radici complesse e coniugate
33
APPUNTI DI ANALISI MATEMATICA
Relazioni tra i coefficienti e le radici di una equazione di secondo grado x1 x 2
34
b
a
x1 x 2
c
a
ax 2 bx c a ( x x1 )( x x 2 )
APPUNTI DI ANALISI MATEMATICA
9 - Matrici, Determinanti, Sistemi di equazioni lineari
Matrici
L’elemento aik si dice di posto pari o dispari se è pari o dispari la somma i+k. Matrice di tipo
m,n:
A
a11
a12
....a1n
a 21
a 22
....a 2 n
.............................
a m1
am2
....a mn
Ogni riga costituisce un vettore riga e si denota con:
ai ai1
ai 2
....ain
Ogni colonna costituisce un vettore colonna e si denota con:
a k1
ak 2
ak
.....
a
km
Si definisce matrice quadrata di ordine n una matrice di tipo (n,n). Gli elementi a11, a22,…,ann
si dicono elementi principali ed il loro allineamento costituisce la diagonale principale.
Si definisce matrice identica di ordine n la matrice quadrata (δik)=I con (i,k=1, 2, …,n) tale che
δik=1 per i=k e δik=0 per i≠k. δik è detto simbolo di Kronecker.
I
1 0 ....0
0 1 ....0
....................
0 0 ....1
Si definisce matrice somma di due matrici A e B dello stesso tipo (m,n) la matrice ottenuta
sommando gli elemementi di egual posto.
Si definisce prodotto di un numero α per la matrice A la matrice (αaik)
Siano A=(aik) e B=(bkp) due matrici rispettivamente di tipo (m,n) e (n,r). Si definisce prodotto
delle due matrici la matrice C di tipo (m,r) il cui elemento generico cip è dato da:
n
cip aik bkp
k 1
Determinante di una matrice quadrata
Sia A una matrice quadrata di ordine n. Si consideri il prodotto degli elementi della diagonale
principale e, tenendo fissi i primi indici, si permutino in tutti i modi possibili i secondi indici; si
ottengono così n! prodotti. Si assume ogni prodotto con il proprio segno o con il segno
opposto rispettivamente se la permutazione è di classe pari o dispari. Si definisce
determinante della matrice A il numero ottenuto dalla somma degli n! prodotti estratti dalla
matrice. La definizione è simmetrica rispetto alle righe e alle colonne. Ad esempio, per una
matrice A del terzo ordine il determinante indicato con:
35
APPUNTI DI ANALISI MATEMATICA
Ha il valore:
a11
a12
a13
a 21
a 22
a 23
a31
a32
a33
a11 a 22 a33 a 23 a32 a12 a 21 a33 a 23 a31 a13 a 21 a32 a 22 a31
Proprietà dei determinanti 1. Un determinante non cambia se nella sua matrice si scambiano le righe con le
colonne
2. Se una linea (riga o colonna) di un determinante è costituita di elementi tutti nulli, il
determinante è nullo.
3. Se si moltiplicano tutti gli elementi di una linea di un determinante per un numero k≠0,
il determinante risulta moltiplicato per k
4. Un determinante si cambia nell’opposto quando si scambiano tra loro due linee
parallele.
5. Eseguendo una qualunque sostituzione nelle righe o nelle colonne di una matrice il
determinante rimane inalterato o si cambia nell’opposto a seconda che le due
sostituzioni sono della stessa classe o di classe diversa.
6. Un determinante con due linee parallele uguali è nullo
7. Se in una matrice quadrata due colonne o due righe sono tra loro proporzionali allora
il determinante è nullo.
8. un determinante non cambia se ad una linea si aggiunge una linea parallela
moltiplicata per un numero qualunque
9. Un determinante è nullo se una linea è combinazione lineare delle rimanenti.
Sviluppo del determinante Si definisce minore complementare di un elemento in una matrice di ordine n la matrice di
ordine n-1 che si ottine dalla matrice data togliendovi la riga e la colonna che si incrociano su
quell’elemento.
Si definisce complemento algebrico di un elemento in una matrice il minore complementare o
il suo opposto rispettivamente se l’elemento è di posto pari o dispari.
Se in una matrice gli elementi di una linea sono tutti nulli tranne uno, il determinante è il
prodotto di quell’elemento per il suo complemento algebrico.
Sistemi di equazioni lineari
Sia x(x1,x2,…,xm) un vettore m-dimensionale in un campo F, reale o complesso, con x Є Vm;
L’insieme Vm costituisce uno spazio vettoriale m-dimensionale; sia Sia y(y1,y2,…,yn) un
vettore n-dimensionale nel medesimo campo F, con y Є Vn e Vn spazio vettoriale ndimensionale. Ogni trasformazione che fa passare da un vettore y Є Vn a un vettore x Є Vm è
espressa da una matrice A di tipo (m,n) di numeri (aik) appartenenti al medesimo campo F,
tale che x = A y (trasformazione lineare).
Valgono le seguenti proprietà:
A y1 y 2 Ay1 Ay 2
per ogni
A(y ) Ay
y Vn
per ogni
y1 , y 2 Vn
e F
Dal prodotto di matrici si ha:
x Ay
x1
a11
a12
....a1n
y1
x2
a 21
a 22
....a 2 n
y2
... ............................. ...
x m a m1 a m 2 ....a mn y n
x1 a11 y1 a12 y 2 ... a1n y n
x 2 a 21 y1 a 22 y 2 ... a 2 n y n
...............................................
x m a m1 y1 a m 2 y 2 ... a mn y n
L’ultima serie di eguaglianze è detta sistema di equazioni lineari.
36
APPUNTI DI ANALISI MATEMATICA
Regola di Cramer per i sistemi di n equazioni lineari in n incognite Si consideri il sistema di n equazioni lineari in n incognite x1,x2,….,xn:
p1 a11 x1 a12 x 2 ... a1n x n
p 2 a 21 x1 a 22 x 2 ... a 2 n x n
...............................................
p n a n1 x1 a n 2 x 2 ... a nn x n
Dove ajk sono i coefficienti delle incognite e pi i termini noti. Si dice soluzione del sistema ogni
n-upla di numeri che forma il vettore x(x1,x2,….,xn) e che verifica simultaneamente tutte le
equazioni del sistema. Il sistema si dice possibile o impossibile a seconda che esistano o
meno delle soluzioni. Se il sistema è possibile si dice determinato o indeterminato
rispettivamente se ammette un numero finito o infinito di soluzioni.
Per la soluzione del sistema si procede
1. scrivendo la matrice A=( ajk ) dei coefficienti, si calcola il determinante Δ di A
2. scrivendo la matrice Axi ottenuta sostituendo ai coefficienti che formano la i-esima
colonna di A i termini noti p1,p2,…pn, si calcola il determinante Δxi di A xi
l’i-esima incognita xi è data da:
xi
xi
Esempio: 31 3 x1 3 x 2 5 x3 2 x 4
10 x1 x 2 x3 x 4
7 3 x1 2 x 2
3 5 x1 4 x 2
A
2
1
3
1
5
1
2
1
3
2
5 4
0
0
0
0
e 66;
Pertanto
xi
Analogamente per le altre incognite.
37
Axi
31
10
3
1
5
1
2
1
7
2
3 4
0
0
0
0
xi 66
1
66
e xi 66;
APPUNTI DI ANALISI MATEMATICA
10 - Integrali
Si dice che la funzione F(x) è una primitiva della funzione f(x) in un intervallo U(x1,x2), se in
tutti i punti di U si ha:
dF ( x)
f ( x)
dx
Primitive e integrali indefiniti
Si definisce integrale indefinito di una funzione f(x) ogni espressione F(x)+C.
Proprietà dell’integrale indefinito d
f ( x)dx f ( x)dx
F ( x)dx F ( x) C
f ( x) f ( x) dx f ( x) dx f ( x) dx
kf ( x)dx k f ( x)dx con k cos tan te
1
Se
f ( x)dx F ( x) C
2
1
2
allora è:
1
f (ax)dx a F ( x) C
f ( x b)dx F ( x b) C
1
f (ax b)dx a F (ax b) C
Integrali delle funzioni elementari n
x dx
x n 1
C
n 1
per n 1
e
x
dx e x C
1
x dx ln x C
x
a dx
sin( x)dx cos( x) C
1 x
cos( x)dx sin( x) C
a
1
cos
sin
2
( x)
dx tg ( x) C
1
dx cot g ( x) C
2
( x)
tg ( x)dx ln cos( x) C
cot g ( x)dx ln sin( x) C
38
1
2
ax
C con a 0
ln(a )
dx arctg ( x) C
1
1
x
dx arctg C
2
a
x
a
1
1
ax
a 2 x 2 dx 2a ln a x C
1
1 x 2 dx arcsin( x) C
1
x
a 2 x 2 dx arcsin a C
1
2
2
x 2 a 2 dx ln x x a C
2
APPUNTI DI ANALISI MATEMATICA
Metodi di integrazione
Metodo di sostituzione Vi sono delle funzioni f(x) integrabili in cui il calcolo della primitiva è semplificato se si
sostituisce nella espressione la variabile x, ponendo x=g(t), dove g(t) è una funzione continua
che ha derivata continua ed ammette funzione inversa. Allora:
dx g ' (t )dt e
f ( x)dx f g (t ) g ' (t ) dt
E’ preferibile talvolta scegliere per la sostituzione della variabile la forma t=h(x) anziché x=g(t).
Esempio Calcolo di:
sin( x) cos( x) dx
Posto sin(x)=t risulta d(sin(x))=cos(x)dx ne consegue:
sin( x) cos( x) dx t dt
1
t2
C sin 2 ( x) C
2
2
Metodo di integrazione per parti Questo metodo è utile quando dobbiamo integrare funzioni esprimibili come prodotto di due
fattori u e v. Ad esempio sono integrabili per parti:
x
k
sin(ax) dx;
x
k
cos(ax) dx;
x
k
e ax dx;
x
k
ln( x) dx;
Siano u=u(x) e v=v(x) due funzioni derivabili, allora:
d (uv) udv vdu
Integrando si ottiene:
uv udv vdu
Per cui la formula di integrazione per parti è:
udv uv vdu
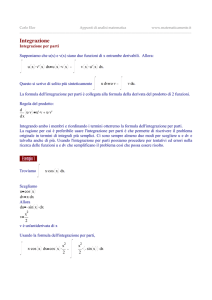
Esempio calcolare
x
2
2
sin( x) dx
Posto u=x , du=2xdx, v=-cos(x). dv= sin(x))dx ne consegue:
x
2
sin( x) dx x 2 d ( cos( x)) x 2 d (cos( x)) x 2 cos( x) cos( x) 2 x dx
x 2 cos( x) 2 x cos( x) dx
1)
Per il secondo integrale si pone u=x, du=dx, v=sin(x), dv=cos(x) dx. Mediante il metodo di
integrazione per parti si ottiene:
x cos( x) dx x sin( x) sin( x) dx x sin( x) cos( x) C '
Sostituendo nella 1) abbiamo:
x
39
2
sin( x) dx x 2 cos( x) 2x sin( x) cos( x) C ' 2 x sin( x) x 2 2 cos( x) C
APPUNTI DI ANALISI MATEMATICA
Integrali definiti
Con riferimento alla figura, viene detto integrale definito della funzione f(x)
b
Nell’intervallo [ab] e si indica con
f ( x)dx
il limite:
a
lim
xi 0
b
n
f ( )x f ( x)dx
i
i 1
i
a
Questo integrale rappresenta graficamente l’area sottesa dalla curva f(x) tra gli estremi a e b.
Proprietà degli integrali definiti b
1)
a
a
f ( x)dx f ( x)dx se a b
b
b
2)
f ( x)dx 0
se a b
a
3)
b
b
a
a
A f ( x)dx A f ( x)dx
b
4)
a
b
5)
b
b
a
a
f1 ( x) f 2 ( x)dx f1 ( x)dx f 2 ( x)dx
b
f ( x)dx f
1
a
2
( x)dx
se
f 1 ( x) f 2 ( x) in ab
a
b
b
b
b
a
a
a
a
6) m(b a ) mdx f ( x)dx Mdx M (b a ) se m f ( x)dx M
7) Pr oprietà del valore medio : se f ( x) continua in ab allora esiste un valore ab tale che :
b
f ( x)dx (b a) f ( )
a
b
8) Se a c b, allora
a
40
c
b
a
c
f ( x)dx f ( x)dx f ( x)dx
APPUNTI DI ANALISI MATEMATICA
Metodi di calcolo degli integrali definiti b
Nell’integrale
f ( x)dx fissiamo l’estremo a e facciamo variare l’estremo b, indicando
a
l’estremo superiore con x e la variabile di integrazione con t si ha:
x
f (t )dt F ( x)
a
Se f(x) è una funzione continua ed è valida la formula precedente si ha dF(x)/dx = f(x); così se
F(x) è una primitiva della funzione continua f(x), è valida la formula:
b
f ( x)dx F ( x)
b
a
F (b) F (a )
a
Metodi di Integrazione Sostituzione di variabile b
Sia dato l’integrale
f ( x)dx , dove f(x) è continua in [ab]; sia x=g(t). Se g(m)=a e g(n)=b, g(t)
a
e g’(t) sono continue nell’intervallo [mn], f [g(t)] è definita e continua in [mn], allora:
b
n
f ( x )dx f g (t ) dt
a
m
Esempio: Calcolo dell’area della superficie di un cerchio di raggio r
Consideriamo un cerchio con centro nell’origine, l’equazione della circonferenza è:
y r 2 x2
Il valore del quarto della superficie che si trova sul primo quadrante è dato dall’integrale:
r
r 2 x 2 dx
0
Per applicare il metodo di sostituzione poniamo: x=r sin(t), dx= r cos(t) dt. Da x=r sin(t) si ha
che per x=0 t=0 mentre per x=r abbiamo t=π/2. Pertanto:
2
r r sin (t ) r cos(t ) dt r
2
2
2
0
2
2
1 sin (t ) cos(t ) dt r
2
0
2
2
cos
2
(t ) dt
0
Impiegando la formula di duplicazione otteniamo:
2
r2 /2 r2
dt
t
2 0
2
2
1 1
r cos (t ) dt r cos(2t )
2 2
0
0
2
2
2
r2
r2
cos(
2
t
)
dt
0
2
2
2
2
cos(2t )dt
0
Per risolvere l’integrale si pone u=2t, e quindi è du=2dt; dt=du/2; per t=0 u=0 mentre per t=π/2
si ha u=π/2. Percui:
2
1
1
cos(u )du sin(u ) 0
2 0
2
0
cos(2t )dt
0
e
r
r 2 x 2 dx
0
Pertanto, l’area del cerchio diventa
41
r
2
.
r2
4
APPUNTI DI ANALISI MATEMATICA
Metodo di integrazione per parti Siano u=u(x) e v=v(x) due funzioni continue e derivabili in [ab], allora:
d (uv) udv vdu
Per cui la formula di integrazione per parti è:
b
b
udv uv a vdu
b
a
a
Integrali Impropri
Integrali con estremi infiniti Sia f(x) una funzione definita e continua per x tale che
limite:
a x ; se esiste e converge il
b
lim f ( x )dx
b
a
Questo limite si chiama integrale improprio di f(x).Se tale limite non esiste finito allora
l’integrale improprio non esiste o diverge.
Integrale di una funzione discontinua Sia f(x) una funzione definita e continua per a x c ; se nel punto c o non è definita o
presenta una discontinuità, allora l’integrale della funzione in c è definito come:
c
a
b
f ( x)dx lim f ( x)dx
b c
a
Se tale limite non esiste finito allora l’integrale improprio non esiste o diverge.
42
APPUNTI DI ANALISI MATEMATICA
11 - Funzioni di più variabili
Funzioni reali di più variabili reali
Se all’insieme ordinato di n valori reali delle variabili indipendenti x. y, z,…t corrisponde un
solo valore della variabile reale w, si dice che w è una funzione delle variabili indipendenti x. y,
z,…t e si scrive w=f(x. y, z,…t).
L’insieme delle n-uple ordinate di valori reali o punti costituisce uno spazio a n dimensioni sul
campo reale, indicato con Rn e la n-upla ordinata con x(x1, x2,…,xn). La funzione può allora
essere scritta come w=f(x) con xЄ Rn.
Negli spazi Rn si definisce distanza fra due punti x e y il numero reale:
x1 y1 2 .... xn y n 2
x y
Siano x0 un punto ed r un numero positivo: l’insieme dei punti x che soddisfano la relazione
||x- x0||≤r forma un cerchio in R2 , una sfera in R3 , un’iposfera in Rn .
Si definisce intorno circolare di x0 di raggio r l’insieme ||x- x0||<r e si indica con U(x0, r).
Derivate parziali, differenziale totale
Si faccia riferimento alle figure riportate nel seguito.
Incremento parziale ed incremento totale Si considerino la funzione z=f(x,y) e la linea A’PA definita dall’intersezione della superficie
z=f(x,y) con il piano y=y0.
Si consideri la linea B’PB definita dall’intersezione della superficie z=f(x,y) con il piano x=x0.
Se x subisce un incremento Δx, l’incremento corrispondente di z, indicato con Δxz=f(x+ Δx,y)f(x,y), è detto incremento parziale di z rispetto a x.
Se y subisce un incremento Δy, l’incremento corrispondente di z, indicato con Δyz=f(x, y+ Δy)f(x,y), è detto incremento parziale di z rispetto a y.
Se si danno contemporaneamente incrementi di Δx e Δy , l’incremento corrispondente di z,
indicato con Δz=f(x+ Δx, y+ Δy)-f(x,y), è detto incremento totale di z.
Derivate parziali La derivata parziale di z rispetto ad x è:
lim
x 0
xz
f ( x x , y ) f ( x , y )
lim
x
0
x
x
E si indica con z’x , f’x(x,y), δf/δx
La derivata parziale di z rispetto ad y è:
lim
yz
y 0
E si indica con z’y , f’y(x,y), δf/δy
43
y
lim
y 0
f ( x , y y ) f ( x , y )
y
APPUNTI DI ANALISI MATEMATICA
Differenziale totale Si supponga che le derivate parziali della funzione f(x,y) esistano e siano continue nel punto
(x0,y0); l’incremento totale Δz della funzione può allora essere scritto come:
z
f ( x, y )
f ( x, y )
x
y 1 x 2 y
y
x
Dove α1 e α2 tendono a zero quando Δx e Δy tendono a zero. Indicando rispettivamente con
dx e dy gli incrementi Δx e Δy delle variabili indipendenti, supposto che le derivate parziali di
f(x,y) siano continue nel punto considerato, si dice che la funzione z è differenziabile nel
punto (x0,y0) se l’incremento totale Δz può essere scritto come:
z
f ( x, y )
f ( x, y )
dx
dy 1 dx 2 dy
y
x
Ponendo:
dz
f ( x, y )
f ( x, y )
dx
dy
x
y
dz è detto differenziale totale.
Per le funzioni di più variabili il differenziale totale è:
dz
f
f
f
dx1
dx 2 ...
dx n
x1
x 2
x n
Derivata parziale e differenziale totale di una funzione composta
Sia z=F(u,v) con u=f(x,y) e v=g(x,y); se si suppone che tutte le derivate parziali di F(u,v), f(x,y)
e g(x,y) siano continue, allora le derivate parziali rispetto ad x e y sono:
z z u z v
x u x v x
Il differenziale totale è dato da:
dz
z z u z v
y u y v y
z
z
du
dv
u
v
Derivate parziale e differenziale totale di ordine superiore
Derivate parziali Sia z=f(x,y) e siano δz/δx e δz/δy ancora funzioni di x e y.Si dice derivata parziale di n-esimo
ordine la derivata prima della derivata di (n-1)-esimo ordine; così:
nz
x m y nm
è una derivata di n-esimo ordine con z derivata m volte (m<n) rispetto a x e n-m volte rispetto
a y.
Differenziale totale Sia z=f(x,y) e sia d(dz) ancora funzione di x e y. Si dice differenziale totale di ordine n-esimo il
differenziale primo del differenziale di ordine (n-1):
d d n 1 f ( x, y ) d n f ( x, y )
Superfici di livello
Sia dato nello spazio R3 un campo FЄR nel quale è definita una funzione reale u=u(x, y, z); si
dice allora che in F è definito un campo scalare. Si considerino i punti del campo F per cui:
u ( x, y , z ) k
k cos tan te
L’insieme di questi punti costituisce una superficie detta superficie di livello. Nello spazio R2 si
parla di linee di livello.
44
APPUNTI DI ANALISI MATEMATICA
Derivata secondo una direzione data, Gradiente
Derivata secondo una direzione data Si supponga che la funzione u=u(x, y, z) sia definita in un campo F continuo e abbia derivate
continue. Consideriamo un punto P(x, y,z)ЄF e tracciamo da P un vettore n i cui coseni
direttori sono cos(α), cos(β) e cos(γ); Consideriamo su n un’altro punto
P1(x+Δx,y+Δy,z+Δz)ЄF in modo che:
n x 2 y 2 z 2
se si indica con Δu l’incremento totale della funzione al passaggio da P a P1 allora
u
n 0 n
lim
si dice derivata della funzione nel punto P(x, y,z) secondo la direzione del vettore n e si indica
con:
u
u
u
u u
lim
cos( ) cos( ) cos( )
n
0
n x
n
y
z
Gradiente Si consideri la funzione u=u(x, y, z) precedentemente definita; in ciascun punto delcampo F si
definisce un vettore, indicato con grad(u) le cui componenti sono:
grad (u )
u u
u
i
j k
x y
z
Legame tra gradiente e derivata secondo una direzione. Sia dato un campo scalare u=u(x, y, z) e sia definito in questo campo il campo dei gradienti.
allora la derivata secondo la direzione del vettore n è eguale alla proiezione del vettore
grad(u) sul vettore n.
Proprietà del gradiente 1. La derivata di una funzione u in un punto P secondo la direzione di un vettore n ha
valore massimo se la direzione coincide con quella del gradiente
u
grad (u )
n
2. La derivata secondo la direzione normale al vettore grad(u) è nulla
3. Il gradiente della funzione u(x, y, z) in un dato punto è diretto lungo la normale alla
superficie di livello passante per il punto dato.
45
APPUNTI DI ANALISI MATEMATICA
Esempio Data la funzione u=x2+y2+z2 , determinare il grad(u) nel punto P(1, 1, 1) e la derivata in P
nella direzione di grad(u):
Soluzione:
u
2x
x
u
2y
y
u
2z
z
grad (u ) 2 xi 2 yj 2 zk
grad (u p ) 2i 2 j 2k
grad (u p ) 12
Coseni direttori di grad (u p ) :
cos( )
per cui
46
1
3
cos( )
1
3
cos( )
1
1
1
u
2
2
2
12 grad (u )
n
3
3
3
1
3
APPUNTI DI ANALISI MATEMATICA
12 - Integrali multipli, curvilinei, di superficie e operatore
Hamiltoniano
La nozione dell’integrale multiplo è una estensione della nozione d’integrale definito di
funzioni di una variabile al caso di funzioni di due variabili.
Integrale doppio
Se la funzione f(x, y) è continua in un campo chiuso U, campo di integrazione, per f(x, y)≥0,
l’integrale doppio si indica come
f ( x, y)dxdy
U
ed è uguale al volume V della figura limitata dalla superficie z=f(x, y), dal piano z=0 e dalla
superficie le cui generatrici sono parallele all’asse 0z e che ha per base il contorno di U.
Proprietà 1.
f ( x, y) f
1
2
U
2.
( x, y )dxdy f 1 ( x, y )dxdy f 2 ( x, y )dxdy
U
c f ( x, y)dxdy c f ( x, y)dxdy
U
U
con c cos tan te
U
3. Se il campo U è costituito da due campi U1 e U2 non aventi punti interni in comune e
se f(x, y) è continua in tutti i punti di U, allora
f ( x, y)dxdy f ( x, y)dxdy f ( x, y)dxdy
U
U1
U2
Integrale curvilineo
Si consideri un punto P(x, y, z) che si muove lungo una curva L nello spazio, da un punto A
ad un punto B (vedere figura sopra) sollecitato da una forza F che varia di intensità e
direzione mentre P si muove lungo la curva. Si divida la curva L in parti arbitrarie e si indichi
con ΔSi il vettore spostamento di estremi Mi e Mi+1 . Si consideri il prodotto scalare F ΔSi della
forza nel punto Mi per lo spostamento relativo, se consideriamo le componenti lungo gli assi
abbiamo:
Fi S i Fxi ( x, y, z )xi Fy i ( x, y, z )y i Fz i ( x, y, z )z i
Si consideri la somma:
47
APPUNTI DI ANALISI MATEMATICA
n
Fx ( x, y, z )x
i
i 1
i
Fy i ( x, y, z )y i Fz i ( x, y, z )z i
1)
Per n , xi 0 ( anche xi e xi tendono a zero); se esiste finito il limite della 1)
esso esprime il lavoro W della forza F lungo la curva L tra i punti A e B.
n
W lim Fxi ( x, y, z )xi Fy i ( x, y, z )y i Fz i ( x, y, z )z i
x i 0
yi 0 i 1
z i 0
Questo limite si chiama integrale curvilineo di Fxi , Fyi , Fzi lungo la curva L
e viene indicato come:
W Fxi ( x, y, z )dxi Fyi ( x, y, z )dyi Fzi ( x, y, z )dzi Fds
L
L
Se la curva è chiusa l’integrale curvilineo viene indicato con
W Fds
Proprietà 1. Un integrale curvilineo è definito dall’espressione integrando, dalla forma della curva
di integrazione e dal senso di integrazione.
2. Dividendo la curva L in elementi L1, L2,…Ln si ha:
Fds Fds Fds ..... Fds
L
L1
L2
Ln
Integrale di superficie
In un sistema ortogonale Oxyz si considerino un campo scalare F ed una superficie σ
delimitata da una curva. Per la superficie σ sia definito in ogni suo punto P un senso positivo
mediante un vettore normale unitario n(P). Si supponga che in ogni punto P di σ sia definito
un vettore F; si divida arbitrariamente σ in aree Δσi , si prenda un punto arbitrario Pi in ogni
elemento Δσi , e si consideri
n
F n
i
i 1
i
Il limite di tale somma relativa a tutte le aree Δσi ,quando Δσi ->0 si dice integrale di superficie:
lim
i 0
n
F n
i 1
i
F n d
i
L’integrale di superficie è detto anche flusso del campo vettoriale F attraverso la superficie σ.
Proprietà: 1. Se si divide σ in elementi σ1, σ2,… ,σn allora:
F n d F n d
F n d
1
1
2
... F n d n
n
2
2. Esprimendo il vettore n ed il vettore F per mezzo delle loro proiezioni suli assi
coordinati:
n i cos( ) j cos( ) k cos( ); F iFx jFy kFz
Si ha:
F n d F
x
Dove:
48
cos( ) Fy cos( ) Fz cos( ) d Fx dydz Fy dzdx Fz dxdy
dydz d cos( ); dxdz d cos( ); dxdy d cos( );
APPUNTI DI ANALISI MATEMATICA
Divergenza, Rotore, Operatore Hamiltoniano
Divergenza di una funzione vettoriale Si consideri un volume finito V di forma qualsiasi e si indichi con σ la sua superficie. Si divida
arbitrariamente il volume V in un certo numero di parti ΔV1, ΔV2,…, ΔVn, aventi superfici Δσ1,
Δσ2,…, Δσn; per la superficie i-esima si consideri il rapporto:
F
i
ni d i
Vi
Con Fi vettore relativo all’area dσi; ni vettore unitario normale all’area dσi.
Se il limite di tale rapporto esiste questi rappresenta la divergenza di F:
F
i
lim
Vi 0
n i d i
Vi
div( F )
La divergenza di F rappresenta il flusso uscente da Vi per unità di volume. Essa può
variare da punto a punto, quindi div(F) è una funzione scalare delle coordinate e rappresenta
una proprietà locale di un campo vettoriale.
Se F è espressa in funzione di coordinate ortogonali (x, y, z) con Fx, Fy, Fz derivabili, preso un
volume Vi 0 di lati Δx, Δy, Δz, il flusso per unità di volume uscente da Vi è:
div ( F )
Fx Fy Fz
x
y
z
Rotore di una funzione vettoriale Si consideri una linea C nello spazio che delimita una superficie σ come rappresentato in
figura:
Si suddivida arbitrariamente la superficie σ in un gran numero di aree Δσ1, Δσ2,…, Δσn. Presa
la superficie i-esima (Δσi ) si consideri il contorno Ci e l’integrale
F ds calcolato nel punto P
Ci
49
i
APPUNTI DI ANALISI MATEMATICA
appartenente a Δσi ed il vettore unitario n normale a Δσi. n si manterrà costante per
i 0 . Nel calcolo dell’integrale il verso di n e quello di percorrenza lungo Ci devono
soddisfare la regola della mano destra. Consideriamo ora il rapporto:
F ds
Ci
i
Ed il suo limite per i 0 , il valore del limite, se esiste, è una grandezza scalare
associata al punto Pi e alla normale n. Moltiplicando il valore di questo limite per n si ottiene
un vettore che prende il nome di rotore e si indica con:
rot ( F ) lim
i 0
F ds
Ci
i
n
Proprietà:
1. Teorema di Stokes
F ds rot ( F ) n d
C
2. Se F è espressa in funzione di coordinate ortogonali (x, y, z) con Fx, Fy, Fz derivabili,
preso un punto Pi del campo F ed un’area i 0 il rot(F) in Pi in funzione delle
coordinate è:
F Fy Fx Fz Fy Fx
j
rot ( F ) i z
k
y
z
z
x
x
y
Operatore Hamiltoniano Se si considera il simbolo:
i
j k
x
y
z
Come un vettore simbolico detto operatore Hamiltoniano od operatore nabla, il gradiente, il
rotore e la divergenza espressi in coordinate cartesiane possono essere scritte come:
grad ( f ) f ; rot ( F ) F ; div( F ) F
F , permette di scrivere il rotore sottoforma di determinante:
50
i
j
k
x
y
z
Fx
Fy
Fz
APPUNTI DI ANALISI MATEMATICA
Formule di analisi vettoriale concernenti grad, rot div grad ( f 1 f 2 ) grad ( f 1 ) grad ( f 2 ) con f 1 e f 2 funzioni scalari
grad ( f 1 f 2 ) f 1 grad ( f 2 ) f 2 grad ( f 1 )
div ( F1 F2 ) div( F1 ) div( F2 ) con F1 e F2 funzioni vettoriali
rot ( F1 F2 ) rot ( F1 ) rot ( F2 )
div ( fF ) f div( F ) Fgrad ( f )
div (rot ( F )) 0
rot ( fF ) f rot ( F ) grad ( f ) F
rot ( grad ( f )) 0
F n dS div( F )dV
S
V
F ds rot ( F ) n dS
C
51
S
APPUNTI DI ANALISI MATEMATICA
13 - Equazioni differenziali e calcolo operazionale
Si chiama equazione differenziale ordinaria un’equazione che stabilisce una relazione tra la
variabile indipendente x, la funzione incognita y=f(x) e le sue derivate y’, y’’,…, yn:
F ( x, y, y ' , y '' ,..., y ( n ) ) 0
Si dice ordine di una equazione differenziale l’ordine massimo della derivata che vi compare.
Si dice soluzione di un’equazione differenziale una funzione qualsiasi y=f(x) che sostituita
nell’equazione la trasforma in una identità.
Il calcolo operazionale permette di ridurre la soluzione delle equazioni differenziali ordinarie a
semplici operazioni algebriche, includendo automaticamente le condizioni iniziali.
Trasformata di Laplace
Siano s j con α>0 e f(t) una funzione reale definita per t , tale che
f(t)=0 per t<0; f(t) ha proprietà tali che esiste l’integrale:
e
st
f (t )dt F ( s )
0
La funzione F(s) è detta immagine Laplaciana o immagine L o immagine di f(t); f(t) è detta
funzione iniziale. L’immagine L si indica come:
L f (t ) F ( s )
Data l’immagine F(s), esiste una ed una sola funzione f(t) ottenuta attraverso la
trasformazione inversa:
L1 F ( s ) f (t )
Proprietà:
1 ‐ Unicità dell’immagine Se due funzioni continue f1(t) e f2(t) hanno la stessa immagine L allora le due funzioni sono
identicamente uguali.
2 ‐ Linearità dell’immagine Se con ci costante e fi(t) funzione i-esima della variabile reale t, allora:
n
L f (t ) F ( s ); L f i (t ) Fi ( s ) e F ( s ) ci Fi ( s )
1
3 – Proprietà dello spostamento
Se L f (t ) F ( s ) allora è F ( s ) L e t f (t )
4 – Derivazione dell’immagine
Se L f (t ) F ( s ) allora è F t n f (t ) 1
5 – Immagine delle derivate
n
d n F ( s)
ds n
Se L f (t ) F ( s ) allora è F f ( n ) (t ) s n F ( s ) s n 1 f (0) ... f ( n 1) (0)
6 – Immagine dell’integrale
Se L f (t ) F ( s ) , indicando l’integrale di f(t) con:
52
APPUNTI DI ANALISI MATEMATICA
D
1
f (t ) f (t )dt D 1 f (0 )
t
0
allora è:
L D 1 f (t )
1
F ( s ) D 1 f (0 )
s
s
Il termine D f (0 ) è la costante di integrazione ed è uguale al valore dell’integrale nel
punto t=0. Per l’integrale i-esimo si ha:
L D n f (t )
D n f (0 )
F ( s ) D 1 f (0 )
...
s
sn
sn
7 – Proprietà del valore finale Se f(t) e f’(t) ammettono trasformata di Laplace e se L[f(t)]=F(s) ed esiste il limite di f(t) per
t , allora è:
lim s F ( s ) lim f (t )
s 0
t
8 – Proprietà del valore iniziale Se f(t) e f’(t) ammettono trasformata di Laplace e se esiste il limite di sF(s) per s ,
allora è:
lim s F ( s ) lim f (t )
s
t 0
9 – Proprietà dell’integrazione complessa Se L[f(t)]=F(s) e se esiste il limite di f(t)/t per
t 0 , allora è:
f (t )
L
F ( s ) ds
t s
10 – Teorema di Convoluzione Se L[f1(t)]=F1(s) e L[f2(t)]=F2(s) , allora per
0
si ha:
L f 1 (t ) f 2 (t ) d F1 ( s ) F2 ( s )
0
t
Trasformate di Laplace
N°
Funzione f(t) per t≥0
1
u 0 (t )
2
1
3
u 1 (t a )
4
u 1 (t ) u 1 (t a )
5
tu 1 (t )
53
L[f(t)]
1
1
s
1 as
e
s
1
1 e as
s
1
s2
APPUNTI DI ANALISI MATEMATICA
6
1
t n 1
n 1!
7
e at
8
1
t n 1e at
n 1!
9
10
11
12
13
14
15
16
17
18
19
20
21
s a n
1
1 e at
a
1
b at
a bt
1
e
e
ab b a
ba
1
b( a ) at a ( b) bt
e
e
ab
ba
ba
1
e at e bt
ba
1
ae at be bt
ab
1
a e at b e bt
ba
e at
e bt
e ct
(b a)(c a ) (c b)(a b) (a c)(b c)
a e at
b e bt c e ct
(b a)(c a ) (c b)(a b) (a c)(b c)
1
at 1 e t
2
a
1
1 e t ate t
2
a
1
e t a(a )te t
a2
o a 2 1 a o t b 2 1b o bt
e
e
ab
a ( a b)
b( a b)
1 o t o ( a b)
1 1 o at
1
e
2
ab
a a2
ab
(ab)
1 1 o bt
1
e
ab
b b2
22
sin(t )
23
cos(t )
54
1
sn
1
sa
1
1
s(s a)
1
s ( s a )( s b)
s
s ( s a )( s b)
1
( s a)( s b)
s
( s a )( s b)
s
( s a )( s b)
1
( s a )( s b)( s c)
s
( s a )( s b)( s c)
1
s (s a)
1
s(s a) 2
s
s(s a) 2
2
s 2 1s 0
s ( s a )( s b)
s 2 1s 0
s 2 ( s a )( s b)
s 2
s
2
s 2
2
APPUNTI DI ANALISI MATEMATICA
24
2 2
sin t
arctg
25
sin(t )
26
27
1
2
s sin( ) cos( )
s2 2
1
2
s s 2
1 cos(t )
2 2
cost
2
arctg
e at
28
s
s 2
2
2
1
c 2
2
s
s s2 2
sin t
1
s a s 2 2
arctg
a
29
30
31
1 at
e sin(bt )
b
1
e nt sin 1 2 t
2
n 1
s a 2 b 2
1
s 2 n s n
2
b
s a 2 b 2
e t sin bt
b
a
1
1
e t sin bt
2
2
2
2
a b
b a b
b
arctg
a
1
1
2
e nt sin n 1 2 t
2
n n 1 2
s
s a 2 b 2
arctg
33
34
arccos
35
55
a2 b2
1
b
2
sa
e at cos(bt )
a 2 b 2
32
1
a 2 b 2 e t sin bt
a2 b2
b
b
arctg
arctg
a
a
1
s s a b 2
2
1
s s 2 n s n
2
s
s s a b 2
2
2
APPUNTI DI ANALISI MATEMATICA
36
e ct
e at sin(bt )
(c a ) 2 b 2 b (c a ) 2 b 2
s c s a 2 b 2
b
arctg
ca
1
e ct
c ( a 2 b 2 ) c (c a ) 2 b 2
37
1
e
b a b
2
sin(bt )
at
(c a ) b
2
2
1
s s c s a b 2
2
2
b
b
arctg
ca
a
(c )e ct
c ( a 2 b 2 ) c (c a ) 2 b 2
arctg
38
s
( a ) 2 b 2 e at sin(bt )
b a b
2
2
(c a ) b
2
s s c s a b 2
2
2
b
b
b
arctg
arctg
a
a
ca
arctg
39
1
2
0 1 a 2 b 2 1 a 0 2 at
e sin(bt )
c 2 bc b 2 1 2a 2
b 1 2a
b
arctg
arctg 2
2
a
a b 1a 0
c2 a2 b2
s 2 1s 0
s s a b 2
2
Soluzione delle equazioni differenziali con il metodo operazionale
Sia data l’equazione differenziale lineare di ordine n a coefficienti costanti:
a0
d n x(t )
d n 1 x(t )
dx(t )
a
... a n 1
a n x(t ) f (t )
1
n
n 1
dt
dt
dt
1)
Che verifica le condizioni iniziali:
( n 1 )
x(0) x0 , x' (0) x' 0 ,......, x ( n 1) (0) x0
2)
Indicando con X(s)=L[x(t)], F(s)=L[f(t)], supponendo che esistano le immagini della soluzione
dell’equazione 1) e delle sue derivate fino all’ordine n, si determina lequazione ausiliaria della
1):
a 0 s n X ( s ) s n 1 x(0) s n 2 x' (0) ... x n 1 (0)
a1 s
n 1
X (s) s
n2
x(0) s
n 3
x' (0) ... x
.........................................................
a n 1 sX ( s ) x(0) a n X ( s ) F ( s )
Dove l’incognita è X(s). Si scrive la 3) nella forma:
56
n2
(0)
3)
APPUNTI DI ANALISI MATEMATICA
X ( s ) a 0 s n a1 s n 1 ... a n 1 s a n
a0 s
n 1
x(0) s
n2
x' (0) ... x
n 1
(0)
a1 s n 2 x(0) s n 3 x' (0) ... x n 2 (0)
.........................................................
a n 2 sx(0) x' (0) a n 1 x(0) F ( s )
Si pone:
Q( s ) a 0 s n a1 s n 1 ... a n 1 s a n
P( s ) a 0 s
n 1
x(0) s
n2
4)
x' (0) ... x n 1 (0) a1 s n 2 x(0) s n 3 x' (0) ... x n 2 (0)
... a n 2 sx(0) x' (0) a n 1 x(0)
La 4) diviene:
X ( s )Q( s ) P ( s ) F ( s ) da cui
X ( s)
P(s) F ( s)
Q( s) Q( s)
e quindi
x(t ) L1 X ( s )
Esempio:
Risolvere l’equazione differenziale:
d 2 i di
i 0
dt 2 dt
Con le seguenti condizioni iniziali:
i (0) ;
di
(0) 1
dt
Soluzione: dalla 4), l’equazione ausiliaria è:
I ( s )( s 2 s 1) 1 da cui I ( s )
1
( s s 1)
2
I(t)=L-1[I(s)] si ottiene dalla tabella riportata precedentemente (formula 30), ponendo:
2 n 1
2
n 1
1
n 1
2
Si ha:
i (t )
1
1
57
1
4
e
1
t
2
1
t
3
1
sin 1 t 1.15 e 2 sin
t
4
2
APPUNTI DI ANALISI MATEMATICA
14 – Serie
Il concetto di serie, attraverso un passaggio al limite,permette di estendere la nozione
elementare di somma per un numero finito ad un numero infinito di termini.
Serie Numeriche
Sia data una successione {xn} di numeri reali; si dice serie l’espressione:
x1 x 2 ... x n ...
Che si indica anche con i simboli
x
n 1
n
oppure
x
n
, I numeri x1 x 2 ... x n ... sono
detti termini della serie. La somma di un numero finito n dei primi termini della serie si dice
somma parziale e si indica come:
x1 x 2 ... x n ... s n
Se esiste finito il limite lim s n esso si dice somma della serie
indica come
x
n
x
n
n
x
n
, la quale converge e si
S se il limite è infinito allora si dice che la serie diverge e la si indica con
Proprietà:
1. La soppressione di un numero finito di termini di una serie non influisce sulla sua
convergenza.
2. Se
x
S con S finito, anche la serie
n
costante.
3. Se
x
n
c x
n
S e y n S ' con S ed S’ finiti allora
converge:
x
n
c x
n
c S con c
yn S S '
4. Se una serie converge , il suo termine generale xn tende a zero per n tendente
all’infinito ( x n 0 per n (condizione necessaria di convergenza9
5. Condizione necessaria e sufficiente affinché una serie
x
n
converge è che ad ogni
ε>0 si possa determinare v=v(ε) tale che per ogni n≥v la somma di p termini (p≥1)
consecutivi a quello di posto n sia minore di ε :
x n 1 x n ... x n p
6. Si dice che una serie
x
x
n
converge assolutamente quando converge la serie
n
7. Se una serie è assolutamente convergente, essa converge anche in senso ordinario
Alcune serie numeriche
Serie di Mengoli:
1
n (n 1) 1
n 1
Serie Armonica:
1
n
n 1
58
APPUNTI DI ANALISI MATEMATICA
1
n
Serie Geometrica: q 1 q
n 0
1 e 1
per q 1
per q 1
per q 1
per q 1
Criteri di convergenza della serie a termini positivi Criterio del confronto x e u
Siano date due serie
n
n
se xn ≤ un e se
u
n
converge, allora anche
x
n
converge.
Criterio del rapporto Se in una serie
x
n
il rapporto
x n 1
A finito per n , allora la serie converge se
xn
x n 1
x
1 , diverge se lim n 1 1 . Nel caso che il limite sia 1 non si può affermare nulla.
n x
n x
n
n
lim
Criterio della radice Se per la serie
x
n
la radice n-esima n x n A finito per n , allora la serie converge
se lim n x n 1 , diverge se lim n x n 1 . Nel caso che il limite sia 1 non si può affermare
n
n
nulla.
Serie di funzioni
Serie di potenze nel campo reale e complesso Si dice serie di potenze in z con centro in a (z ed a reale o complesso) ogni serie del tipo
c
n
( z a) n
Con cn coefficienti reali o complessi dei termini della serie. Esistono serie di potenze che:
1. convergono per ogni valore di z
2. convergono in qualche punto distinto dal centro ma non convergono in tutto il piano
complesso
3. convergono solo nel centro
Serie di Taylor e di Mac Laurin Sia
f ( x) definita per x0 x x0 h (oppure x0 h x x0 ) ed ammetta derivate destre
(oppure sinistre) f
(n)
( x0 ) nel punto x0 , di qualunque ordine n. La serie di Taylor è:
h n f ( n ) ( x0 )
n!
Se x 0 0 si trova la Serie di Mac Laurin:
x n f ( n ) (0)
n!
59
APPUNTI DI ANALISI MATEMATICA
Sviluppi in serie di funzioni elementari sul campo reale Funzione
Intervallo di
convergenz
a
Sviluppo in Serie
x
x x2
xn
...
...
1! 2!
n!
2
x ln(a)n ...
x ln(a ) x ln(a )
1
...
1!
2!
n!
1
ex
ax
2
3
x
n
ln(x)
1 x 1
x 1 1 x 1 1 x 1
...
...
2 x
3 x
x
n x
ln( x)
ln(a )
ln(1 x)
x
2
sin( x)
3
x2 x3
xn
... (1) n 1
...
2
3
n
x3 x5
x 2 n 1
... (1) n
...
x
2n 1!
3! 5!
x2 x4
x 2n
... (1) n
...
2n !
2! 4!
x
arcsin( x)
x3 1 3 x5 1 3 5 x7
...
6 24 5 246 7
x3 1 3 x5 1 3 5 x7
x
...
2
6 24 5 246 7
x3 x5 x7
x 2 n 1
... (1) n
...
x
2n 1
3
5
7
arctg ( x)
1
2
n
xa 1 xa
1 x a
(1) n 1 x a
...
0 x 2a
a
n a
2 a
3 a
cos( x)
arccos(x)
x
x
| x | 1
x
x
| x | 1
| x | 1
| x | 1
Sh( x)
x
x3 x5
x 2 n 1
...
...
2n 1!
3! 5!
x
Ch( x)
1
x2 x4
x 2n
...
...
2n !
2! 4!
x
1
(1 x)
1
(1 x)
1
(1 x 2 )
(1 x) m
(1 x)
1
(1 x)
60
1 x x 2 x 3 ... x n ...
| x | 1
1 x x 2 x 3 ... (1) n x n ...
| x | 1
1 x 2 x 4 ... (1) n x 2 n ...
| x | 1
m m
m
1 x x 2 ... x n ...
1 2
n
1 1 3 2n 3 n
1
11 2 113 3
x
x ... (1) n 1
x
...
1 x
2n
246
2
24
246
1
13 2 135 3
1 3 5 2n 1 n
x
x ... (1) n
x
1 x
...
2
24
246
246
2n
| x | 1
| x | 1
| x | 1
APPUNTI DI ANALISI MATEMATICA
m
(1 x)
1
1
x 1 m 2
x ... m x n ...
n
m 2
| x | 1
Formule di Eulero z
Si consideri lo sviluppo di e con z complesso:
ez 1
Ponendo z j si ha:
2 4
... 1
...
2!
3!
4!
2!
4!
e cos( ) j sin( )
e j 1 j
e z e j
2
j
3
z z2
zn
...
...
n!
1! 2!
4
3 5
cos( ) j sin( )
j
3!
5!
e j e e j si ha:
e j e j
cos(
)
e j cos( ) j sin( )
2
da cui
j
j
j
e cos( ) j sin( )
sin( ) e e
2j
Posto j si ottiene
Considerando gli sviluppi di
e e
cos(
)
Ch( )
2
sin( ) j e e jSh( )
2
Serie di Fourier
Tutte le funzioni f (t ) periodiche con periodo T, fisicamente realizzabili, possono essere
sviluppate in serie di Fourier nella forma:
Con
0 2 T
f (t ) a 0 a n cosn 0 t bn sin n 0 t
pulsazione fondamentale; a0, an e bn costanti da determinare. I termini
a n cosn 0 t e bn sin n 0 t sono detti armoniche; le armoniche sono pari o dispari a
seconda che n sia pari o dispari. I coefficienti della serie sono calcolabili tramite le.
a0
1
2
2
0
f (t )dt ; a n
1
2
0
f (t ) cosn 0 t dt ; bn
1
2
f (t ) sin n t dt;
0
0
L’eventuale esistenza di simmetria della funzione f (t ) permette di semplificare il calcolo per
la determinazione dei coefficienti:
1. Una funzione ha simmetria pari se f (t ) f (t ) e la serie è composta solo da termini
in coseno
2. Una funzione ha simmetria dispari se f (t ) f ( t ) e la serie è composta solo da
termini in seno
3. Una funzione ha simmetria per rotazione se f (t ) f (t ) e la serie è composta
solo da armoniche dispari; i coefficienti della serie sono dati da:
61
APPUNTI DI ANALISI MATEMATICA
0 per n pari
an 2
f (t ) cos(n 0 t )dt
0 per n pari
bn 2
per n dispari
f (t ) cos(n 0 t )dt per n dispari
Spesso è conveniente normalizzare i termini della serie ponendo 0 1 . La tabella
successiva riporta gli sviluppi in serie di Fourier per alcune funzioni comunemente usate.
62
APPUNTI DI ANALISI MATEMATICA
Nome
Funzione
Grafico
Sviluppo in serie normalizzato
f (t )
Onda Quadra
4
1
1
cos(t ) cos(3t ) cos(5t ) ...
3
5
Onda Quadra
f (t )
1 2
1
1
sin(t ) sin(3t ) sin(5t ) ...
2
3
5
Onda
Triangolare
f (t )
8
1
1
cos(t ) cos(3t ) cos(5t ) ...
2
9
25
Onda a Denti
di Sega
f (t )
2
1
1
sin(t ) sin( 2t ) sin(3t ) ...
2
3
2
1 cos(t ) cos(2t )
1
2
3
f (t )
2
cos(4t ) ...
15
Semionda
Sinusoidale
raddrizzata
Onda
Sinusoidale
raddrizzata
f (t )
2 2
2
1 cos(2t ) cos(4t ) ...
3
15
Integrale di Fourier
Tutte le funzioni periodiche ed impulsive possono possono essere sviluppate in somme di
funzioni sinusoidali definite tra e . Lo sviluppo di funzioni periodiche e impulsive è
ottenuto mediante le relazioni:
F ( j )
f (t )e jt dt ;
f (t )
1
2
F ( j ) e
jt
d ;
Dette trasformate di Fourier, la prima relazione è detta integrale di Fourier. La distribuzione
delle frequenze delle armoniche della serie e dell’integrale di Fourier formano lo spettro.
63
APPUNTI DI ANALISI MATEMATICA
Lo spettro della serie di Fourier di una funzione è formato da linee (figura sopra) mentr lo
spettro dell’integrale è continuo (figura sotto)
Esempio:
Considerando l’impulso rappresentato nella figura precedente abbiamo:
F ( j )
T / 2
f (t )e
T / 2
jt
dt T
sin T / 2
T / 2
La tabella successiva riporta le trasformate di Fourier per alcune funzioni comunemente usate.
Funzione
Trasformata F ( )
Equazione
Grafico
u 0 (t T )
e jT
1 per t T / 2
f (t )
0 per t T / 2
t
1
f (t ) T
0
64
per t T / 2
per t T / 2
T
sin T / 2
T / 2
sin T / 2
T
T / 2
2
APPUNTI DI ANALISI MATEMATICA
e
tT
cos( 0 t )
65
2T
T 2 1
2
u 0 ( 0 ) u 0 ( 0 )
APPUNTI DI ANALISI MATEMATICA
66


![Via Eugenio Barsanti, 24 - 00146 Roma Telefono [Fax] 06](http://s1.studylibit.com/store/data/004164020_1-c5a7c8484d07a6b1f1c9ad8187f8cd02-300x300.png)