Esercizi per la settimana dal 25 al 29 aprile 2016
ESERCIZI SUGLI INTEGRALI
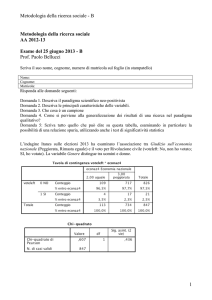
Calcolare
dx
∫2 x 23x+2
−5x+4
3
°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°
2
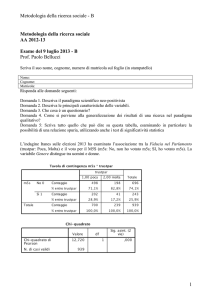
Calcolare ∫ sin x⋅cosx dx
π
2
0
∫
sin 3 ( π )
sin 3 (0)
sin x
2
2
sin x⋅cosx dx=[
] =
−
=
3 0
3
3
1 0 1
= − =
3 3 3
3
π
2
°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°
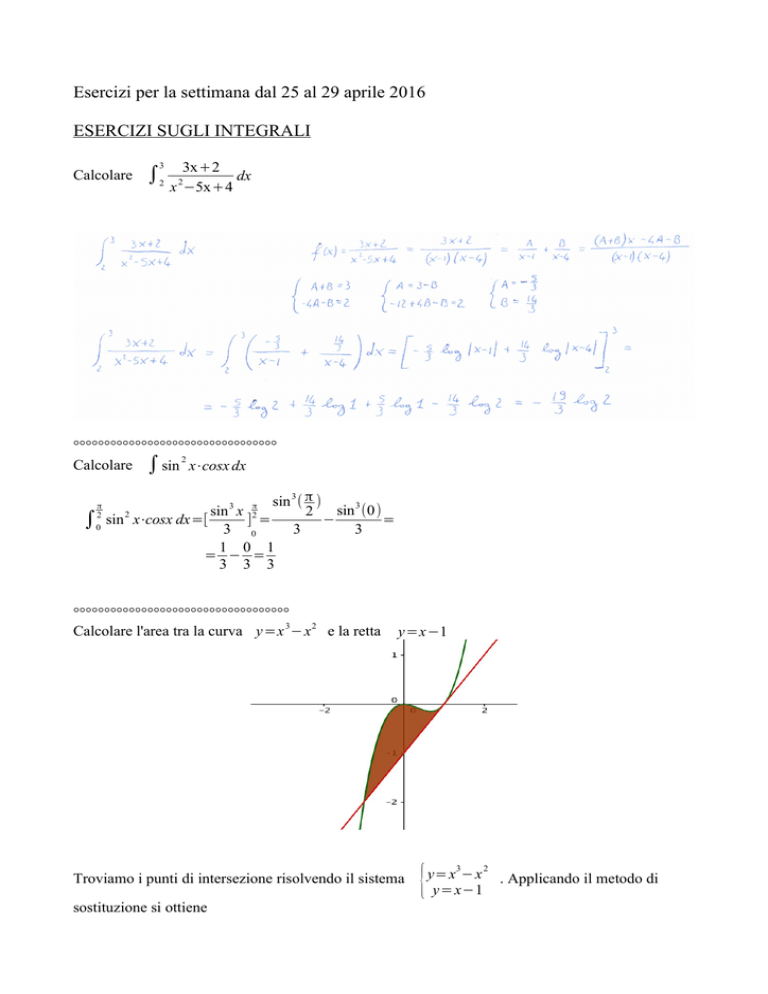
Calcolare l'area tra la curva y=x 3− x 2 e la retta
y=x−1
Troviamo i punti di intersezione risolvendo il sistema
sostituzione si ottiene
{
3
y= x − x
y= x−1
2
. Applicando il metodo di
{
{
{
{
{
2
2
3
2
3
2
x−1= x −x → x−1− x + x =0 → ( x−1)− x ⋅( x−1)=0 → (x−1)⋅( x −1)=0
y= x−1
y= x−1
y= x−1
y= x−1
2
( x−1)⋅( x−1)⋅( x+1)=0 → ( x−1) ⋅( x+1)=0
y= x−1
y= x−1
( x−1)2⋅(x+1)=0 per x=1 or
P (−1,−2) e Q (1,0)
{
x=−1 . Pertanto i punti di intersezione sono
1
1
∫−1 ( x3− x 2) – (x−1) dx=∫−1 x3− x2 −x+1 dx=
L'area quindi è
=[
1
x4 x3 x 2
1 1 1
1 1 1
2
4
− − + x] =( − − +1)−( + − −1)=− +2=
4 3 2
4
3
2
4
3
2
3
3
−1
°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°
Calcolare il volume del solido di rotazione ottenuto ruotando la curva
y=x 2− x 3 tra x=0 e x=1
b
La formula è π⋅∫a [ f (x)]2 dx . Pertanto si ha, nel nostro caso
1
x5 x7 x6 1
+ − ]=
5 7 3 0
1 1 1
21+15−35 π
=π⋅[ + − ]=π⋅
=
5 7 3
105
105
1
π⋅∫0 ( x 2− x 3)2 dx=π⋅∫0 ( x 4+ x 6−2x5 )dx=π⋅[
ESERCIZI DI CALCOLO DELLE PROBABILITA'
PROBLEMA
Alle recenti elezioni hanno votato il 32% degli aventi diritto. L'85% dei votanti ha votato SI il 15%
ha votato NO.
Se viene scelto un cittadino avente diritto al voto, qual è la probabilità che abbia votato NO? Qual è
la probabilità che abbia votato SI?
SOLUZIONE
Ha votato NO se “è andato a votare E ha votato NO”. Chiamiamo
NO l'evento ha votato NO
V l'evento è andato a votare
Pertanto
P (NO )= P (V )⋅P ( NO /V )=0.32⋅0.15=0.048
P (SI )=P (V )⋅P (SI /V )=0.32⋅0.85=0.272
Considerazioni: hanno votato NO il 4,8% degli aventi diritto. Hanno votato SI il 27,2% degli aventi
diritto.
PROBLEMA
L'Italia è composta per il 48,5% da maschi e per il 51,5% da femmine.
Il 27% delle femmine e il 24% dei maschi guardano il telegiornale tutti i tutti.
1. Qual è la probabilità che un cittadino italiano scelto a caso guardi il telegiornale tutti i
giorni?
2. Se un cittadino italiano guarda il telegiornale tutti i giorni qual è la probabilità che sia
maschio?
SOLUZIONE
Chiamiamo TG l'evento “guarda il telegiornale tutti i giorni”
Chiamiamo M l'evento “il cittadino è maschio”
Chiamiamo F l'evento “il cittadino è femmina”
1. Si tratta di una situazione in cui bisogna applicare la formula di disintegrazione. Difatti il
cittadino può guardare il TG tutti i giorni essendo maschio oppure essendo femmina.
Pertanto
P (TG )= P (TG / M )⋅P (M )+P (TG / F )⋅P ( F )=
=0.24⋅0.485+0.27⋅0.515=0.1164+0.13905=0.25545
2. Si tratta di una situazione in cui occorre applicare la formula di Bayes. Difatti si sa che il
cittadino guarda il TG tutti i giorni e si vuole sapere qual è la probabilità che sia dovuto al
fatto che è maschio (probabilità delle cause)
P (M /TG )=
P(TG / M )⋅P (M )
0.1164
=
≈0.455
P (TG / M )⋅M ( M )+ P (TG / F )⋅P (F ) 0.25545
PROBLEMA
Si lancia una moneta 3 volte qual è la probabilità che escano 2 teste?
SOLUZIONE
Abbiamo una sequenza di lanci: 1° lancio, 2° lancio, 3° lancio.
Quindi 2 teste le possiamo ottenere con la sequenza TTC oppure TCT oppure CTT
Pertanto P (3Teste)= P (TTC )+ P (TCT )+ P (CTT )=0.5⋅0.5⋅0.5+0.5⋅0.5⋅0.5+0.5⋅0.5⋅0.5=
=0.125+0.125+0.125=0.375
PROBLEMA
Il 98% delle lampadine prodotte in una fabbrica sono prive di difetti (conformi). Durante la fase di
controllo il 40% delle lampadine difettose e l'1% delle lampadine conformi vengono scartate.
1. Qual è la probabilità che una lampadina sia difettosa e venga scartata?
2. Qual è la probabilità che venga scartata?
3. Se una lampadina viene scartata qual è la probabilità che sia difettosa?
SOLUZIONE
Chiamiamo D l'evento “la lampadina è difettosa”
Chiamiamo C l'evento “la lampadina è conforme”
Chiamiamo S l'evento “la lampadina è scartata”
1. La probabilità che sia difettosa e venga scartata è
P (D∧S )= P (D)⋅P (S / D)=0.02⋅0.4=0.008
2. Una lampadina è scartata se è conforme oppure se è difettosa.
Siamo quindi in una situazione in cui si applica il teorema di disintegrazione
P (S )=P (S /C )⋅P (C )+ P (S / D)⋅P ( D)=0.02⋅0.4+0.98⋅0.01=0.008+0.0098=0.0178
(Durante la fase di controllo vengono scartate circa 2 lampadine)
3. E' una situazione in cui si deve applicare la formula di Bayes.
P (S / D)⋅P (D)
0.0098
P (D /S )=
=
≈0.55
P (S / D)⋅P (D)+P (S /C )⋅P(C ) 0.0178