1.
Un aeroplano percorre con moto uniforme 2475 km in 2 ore e 45 minuti. Calcola la sua velocità in km/h e in m/s.
2 ore e 45 minuti corrispondono a 2,75 h:
v=
2.
2475 km
=
2,75 h
900 km / h
= 900 ⋅
1000 m
=
3600 s
250 m / s
Un’automobile sta compiendo un viaggio. Essa viaggia per i primi 8 minuti a 30 km/h e per i rimanenti 4 minuti a
60 km/h. Calcola qual è la velocità media dell’automobile nell’intero viaggio.
∆ t1 = 8 min =
2
h
15
v1 = 30 km / h
∆ t 2 = 4 min =
1
h
15
v2 = 60 km / h
2
h = 4 km
15
1
∆ x2 = v2 ⋅ ∆ t 2 = 60 km / h ⋅
h = 4 km
15
∆ x1 = v1 ⋅ ∆ t1 = 30 km / h ⋅
vm =
4 km + 4 km 8 km
=
=
2
1
1
h+
h
h
15
15
5
40 km / h
Un metodo più veloce per risolvere l’esercizio consiste nel constatare che la prima velocità viene mantenuta per un tempo doppio
rispetto alla seconda velocità, perciò si può calcolare la velocità media nel seguente modo:
vm =
3.
2 v1 + v2 120 km / h
=
=
3
3
40 km / h
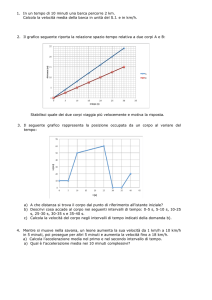
I due grafici riportati in figura rappresentano le distanze percorse da un mobile in funzione del tempo.
a) Descrivi il moto compiuto dai due mobili
I due mobili partono dalla parte opposta di un’unica rotaia. In questa rotaia possiamo distinguere due versi: uno verso destra,
quello che va dal metro 0 al metro 3 e quello verso sinistra, che va dal metro 3 al metro 0.
Il primo mobile si muove verso destra, il secondo mobile verso sinistra. Si incontrano al metro 2.
b) Leggendo il grafico, stabilisci quando i due mobili si incontrano
Dal grafico, si nota che i due mobili si incontrano dopo 3 secondi.
c) Determina la velocità di entrambi
Determino la velocità del mobile 2, calcolando il coefficiente angolare della retta, utilizzando le coordinate dei punti A (3s; 1m)
e B (0s; 3m) e la velocità del mobile 1, calcolando il coefficiente angolare della retta, utilizzando le coordinate dei punti A e O
(0s; 0m):
v1 =
x A − xO 1 m − 0 m
=
=
t A − tO
3s − 0s
0,3 m / s
d) Stabilisci di che moto si tratta in entrambi i casi
Moto rettilineo uniforme.
v2 =
x A − xB 1 m − 3 m
=
=
t A − tB
3s − 0s
− 0,67 m / s
4.
Un sasso è lanciato verso l’alto con una velocità iniziale di 7,0 m/s. Calcola la velocità del sasso dopo 1 secondo dal
lancio.
Si tratta di un moto uniformemente accelerato: considerando v0 = 7 m/s e a = – g = – 9,81 m/s2, nel verso del moto:
− 2, 81 m / s
v = v0 + a t = 7 m / s − 9,81 m / s 2 ⋅ 1 s =
5.
Il grafico rappresenta la velocità di un oggetto in funzione del tempo. Calcola la distanza complessiva percorsa
dall’oggetto.
v
(m/s)
35
0
30
0
25
0
20
0
15
0
10
0
5
0
2
4
6
8
10
12
14
16
18
t (s)
20
Per calcolare la distanza complessiva, devo calcolare l’area della figura compresa tra il grafico del moto e l’asse orizzontale:
x = 25 m / s ⋅ 4 s + 15 m / s ⋅ 4 s +
6.
( 15 + 35 ) m / s ⋅ 4 s 35 m / s ⋅ 8 s
+
=
2
2
400 m
Un corpo parte da fermo con accelerazione uguale a 5 m/s2. Quale velocità raggiunge in 20 secondi? Quanto tempo
impiega a raggiungere la velocità di 90 km/h?
a = 5 m / s2
v0 = 0 m / s
t = 20 s
v = v0 + a t = 0 m / s + 5 m / s 2 ⋅ 20 s =
a = 5 m / s2
v = v0 + a t
v0 = 0 m / s
⇒
t =
100 m / s
v = 90 km / h = 90 ⋅
1000 m
= 25 m / s
3600 s
v − v0
25 m / s − 0 m / s
=
=
a
5 m / s2
5s
7.
Un’auto in 10 secondi passa da una velocità di 20 m/s a una velocità di 26 m/s. Quanto vale l’accelerazione?
v0 = 20 m / s
a=
8.
v = 26 m / s
t = 10 s
v − v0
26 m / s − 20 m / s
=
=
10 s
t
0,6 m / s 2
Un corpo, partendo da una posizione x0 = 0, si muove con un’accelerazione a e, dopo un tempo t, ha raggiunto la
posizione x. Quanto impiegherà a raggiungere la posizione 4x, se si muove con la stessa accelerazione?
x=
1 2
at
2
4x =
1 2
a t1
2
⇒
⇒
t2 =
2x
a
t12 =
2 ⋅ 4x
2 x
=4
= 4t2
a
a
⇒
t1 = 2 t