Diagramma di fase:

Università Politecnica delle Marche, Facoltà di Agraria
C.d.L. Scienze Forestali e Ambientali, A.A. 2010/2011, Fisica
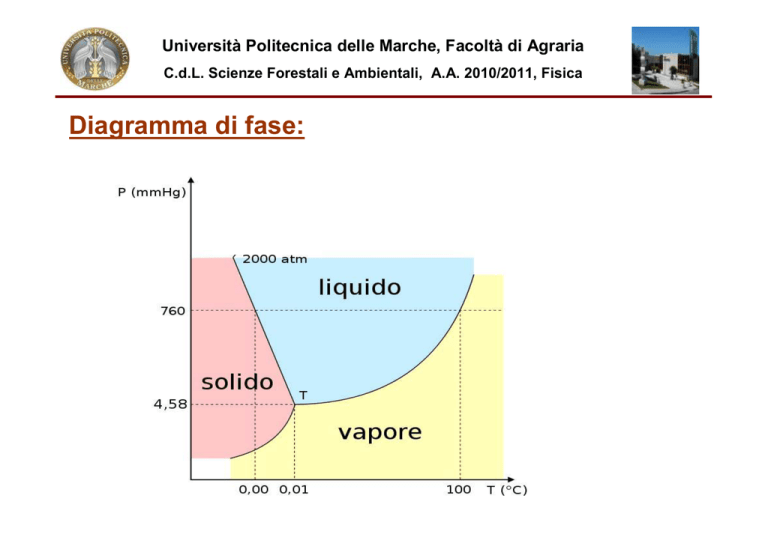
Diagramma di fase:
Università Politecnica delle Marche, Facoltà di Agraria
C.d.L. Scienze Forestali e Ambientali, A.A. 2010/2011, Fisica
Cambiamenti di stato
dell’acqua:
Università Politecnica delle Marche, Facoltà di Agraria
C.d.L. Scienze Forestali e Ambientali, A.A. 2010/2011, Fisica
Università Politecnica delle Marche, Facoltà di Agraria
C.d.L. Scienze Forestali e Ambientali, A.A. 2010/2011, Fisica
Spazio tra i binari dei treni
- per far si che la la dilatazione indotta dalle temperature estive
possa avvenire lungo l'asse del binario stesso
Università Politecnica delle Marche, Facoltà di Agraria
C.d.L. Scienze Forestali e Ambientali, A.A. 2010/2011, Fisica
Dilatazione termica di solidi e liquidi:
temperatura aumenta – corpi si dilatano;
es.: binario dei treni –
spazio tra di loro
Dilatazione lineare: sbarra
∆L = L0 α ∆T
più e lunga, più si dilata
∆L = L − L0 = L0 α ∆T
coefficiente di
dilatazione lineare
es: αFe = 12—10-6 K-1
⇒ L = L0 (1 + α ∆T )
Università Politecnica delle Marche, Facoltà di Agraria
C.d.L. Scienze Forestali e Ambientali, A.A. 2010/2011, Fisica
Dilatazione superficiale:
2
S = L 2 = ( L 0 (1 + α ∆ T )) 2 = L 0 (1 + α ∆ T ) 2 =
2
2
2
2
= L 0 (1 + 2 α ∆ T + α ∆ T ) ≈ L 0 (1 + 2 α ∆ T )
∆ S = S 0 2α ∆ T
⇒
Dilatazione volumica:
3
V = L 3 = ( L 0 (1 + α ∆ T )) 3 = L 0 (1 + α ∆ T ) 3 =
3
= L 0 (1 + 3α ∆ T + 3α 2 ∆ T
⇒
2
3
+ α 3 ∆ T 3 ) ≈ L 0 (1 + 3α ∆ T )
∆ V = V 0 3α ∆ T = V 0 β ∆ T
β – coefficiente di
dilatazione volumica
Università Politecnica delle Marche, Facoltà di Agraria
C.d.L. Scienze Forestali e Ambientali, A.A. 2010/2011, Fisica
Esercizio:
Un cilindro di ferro è riempito fino all’orlo con acqua a 25 gradi
Celsius. Se l’acqua e il cilindro sono riscaldati fino alla temperatura
di 75 gradi Celsius, quale percentuale di acqua fuoriesce dal
cilindro?
Si conoscono: βacqua = 207—10-6 K-1 e βFe = 36—10-6 K-1
Università Politecnica delle Marche, Facoltà di Agraria
C.d.L. Scienze Forestali e Ambientali, A.A. 2010/2011, Fisica
La propagazione del calore:
conduzione
3 meccanismi:
convezione
irraggiamento
La conduzione termica: - corpi a contatto (solidi, liquidi)
acqua calda
Centrale
nucleare
acqua fredda
Università Politecnica delle Marche, Facoltà di Agraria
C.d.L. Scienze Forestali e Ambientali, A.A. 2010/2011, Fisica
Legge di Fourier:
Q
∆T
=kS
∆t
d
calore scambiato
per unità di tempo
conducibilità
termica
S – superficie
d – spessore
∆T – variazione di
temperatura
(potenza scambiata)
k grande - buon conduttore di calore
Es: Conducibilità
termiche a 20°C:
Materiale
legno
acciaio
rame
k piccolo - isolanti
k (W m-1 K-1)
0.13
46
401
Università Politecnica delle Marche, Facoltà di Agraria
C.d.L. Scienze Forestali e Ambientali, A.A. 2010/2011, Fisica
La convezione termica: - fluidi
Aumentando di temperatura, il
fluido a contatto con il fonte di
calore si espande e diminuisce
di densità, generando moti
convettivi in cui il fluido caldo
sale verso l'alto e quello freddo
scende verso il basso.
Brezza di mare:
- durante il giorno dal mare
verso la costa
- durante la notte dalla costa
verso il mare
Università Politecnica delle Marche, Facoltà di Agraria
C.d.L. Scienze Forestali e Ambientali, A.A. 2010/2011, Fisica
L’irraggiamento:
- al contrario della conduzione e della convezione, non prevede
contatto diretto tra gli scambiatori, e non necessita di un mezzo per
propagarsi;
- la trasmissione di energia avviene attraverso l'emissione e
l'assorbimento di radiazione elettromagnetica.
L’effetto serra è un effetto naturale che rende possibile la vita
sul nostro pianeta: senza la presenza dell’atmosfera la
radiazione solare incidente sulla Terra verrebbe quasi
interamente rimandata verso l’esterno e la temperatura
superficiale sarebbe 35 °C in meno rispetto a quella che
realmente abbiamo.
Università Politecnica delle Marche, Facoltà di Agraria
C.d.L. Scienze Forestali e Ambientali, A.A. 2010/2011, Fisica
Università Politecnica delle Marche, Facoltà di Agraria
C.d.L. Scienze Forestali e Ambientali, A.A. 2010/2011, Fisica
Certi gas chiamati gas serra - il biossido di carbonio o anidride
carbonica (CO2), il metano (CH4), il protossido di azoto (N2O) – sono
trasparenti alla radiazione solare, che quindi li attraversa senza
essere assorbita, ma non a quella emessa dalla Terra – risulta
“l’effetto serra”.
Un aumento della concentrazione dei gas serra
provoca un aumento della radiazione restituita
dall’atmosfera alla superficie terrestre. Risulta un
aumento della temperatura media del pianeta.
Dal 1750 ad oggi:
- L’anidride carbonica (CO2) è aumentata del 31%
e continua a salire dello 0.4% per anno
- Il metano (CH4) è cresciuto del 151%
- Il protossido di azoto (N2O) è cresciuto del 17%
Università Politecnica delle Marche, Facoltà di Agraria
C.d.L. Scienze Forestali e Ambientali, A.A. 2010/2011, Fisica
Gas ideale (perfetto):
non esiste in realtà – idrogeno e elio assomigliano di più a un gas ideale
- le molecole sono puntiformi;
- interagiscono tra loro e con le pareti del recipiente
mediante urti perfettamente elastici (ovvero non vi è
dispersione di energia durante gli urti);
- non esistono forze di interazione a distanza tra le
molecole del gas;
- le molecole del gas sono identiche tra loro e
indistinguibili;
Università Politecnica delle Marche, Facoltà di Agraria
C.d.L. Scienze Forestali e Ambientali, A.A. 2010/2011, Fisica
Variabili di stato:
Per i sistemi a molte particelle (in 2 g di idrogeno ci sono 6—1023
molecole!) non è possibile dare posizione e velocità di ogni
particella.
Si descrive il sistema mediante pochi parametri legati ai valori
medi delle grandezze dinamiche:
Volume
Pressione ⇒ legata al valore medio della variazione della
quantità di moto nell’unità di tempo dovuta agli urti delle
particelle sulle pareti.
Temperatura ⇒ legata al valore medio dell’energia cinetica
delle particelle.
Università Politecnica delle Marche, Facoltà di Agraria
C.d.L. Scienze Forestali e Ambientali, A.A. 2010/2011, Fisica
Pressione, volume e temperatura sono le variabili di stato
o coordinate termodinamiche di un fluido omogeneo.
Legge di Boyle: A temperatura costante, il volume occupato da una
data massa di gas e inversamente proporzionale
alla pressione.
P = costante / V
p
P1, V1
T
P2, V2
T
T
V
Università Politecnica delle Marche, Facoltà di Agraria
C.d.L. Scienze Forestali e Ambientali, A.A. 2010/2011, Fisica
Prima legge di Gay-Lussac (legge di Charles):
P, V1,
T1
P, V2,
T2
A pressione costante, il
volume occupato da una
data massa di gas e
diretamente proporzionale
alla temperatura.
V = costante — T
Seconda legge di Gay-Lussac:
P1, V,
T1
P2, V,
T2
A
volume
costante,
la
pressione di una data massa di
gas
e
diretamente
proporzionale alla temperatura.
P = costante — T
Università Politecnica delle Marche, Facoltà di Agraria
C.d.L. Scienze Forestali e Ambientali, A.A. 2010/2011, Fisica
Combinando la legge di Boyle e le due leggi di Gay – Lussac abbiamo:
PV=nRT
Dove
- l’equazione di stato per il gas perfetto
R = 8.31 J / mol K ;
“n” e il numero di moli n = m / µ
m – massa del gas
µ – massa molare
Es. : 64 g di O2 - 2 moli (µO2 = 32g/mol)
P1 V1 P2 V 2
=
T1
T2
Università Politecnica delle Marche, Facoltà di Agraria
C.d.L. Scienze Forestali e Ambientali, A.A. 2010/2011, Fisica
Primo principio della termodinamica:
p
(pA,VA,TA)
U (A)
A
trasformazione termodinamica,
interazione sistema - ambiente:
L, Q.
(pB,VB,TB)
B
U (B)
V
∆U = Q - L
L > 0 se il lavoro è fatto dal
sistema verso l’esterno.
Q > 0 se il calore è
assorbito dal sistema.
Università Politecnica delle Marche, Facoltà di Agraria
C.d.L. Scienze Forestali e Ambientali, A.A. 2010/2011, Fisica
LAVORO TERMODINAMICO:
a pressione costante
S
∆h
P
P
p
T21
T
p = cost
T2 > T 1
T1
T2
T2
Termostato
Termostato
p
r r
L = F ⋅ ∆s
L = P S ∆h cos 0
F =P S
o
A
B
L = P ∆V
V
Università Politecnica delle Marche, Facoltà di Agraria
C.d.L. Scienze Forestali e Ambientali, A.A. 2010/2011, Fisica
Se P non è costante immaginiamo di dividere la
trasformazione in tante microtrasformazioni, in ciascuna
delle quali si possa ritenere la pressione costante.
L = ∑i Pi ∆Vi
L=
o meglio
P ∆ Vi
∑
lim
i i
∆V → 0
i
p
p
A
Lavoro
A
=
B
B
V
area sotto la
trasformazione
Università Politecnica delle Marche, Facoltà di Agraria
C.d.L. Scienze Forestali e Ambientali, A.A. 2010/2011, Fisica
Calori specifici dei gas:
Per i solidi e i liquidi i calori specifici variano con la
temperatura, ma con buona approssimazione sono gli
stessi per trasformazioni a volume e a pressione costanti.
Per i gas abbiamo calori specifici diversi, per
trasformazioni a volume costante (CV) e a pressione
costante (CP).
CP = CV + R - relazione di Mayer
gas monoatomico:
5
3
CV = R C P = R
2
2
gas biatomico:
5
CV = R
2
7
CP = R
2
Università Politecnica delle Marche, Facoltà di Agraria
C.d.L. Scienze Forestali e Ambientali, A.A. 2010/2011, Fisica
Variazione dell’energia interna ∆U:
trasformazione isocora
p
B
L=0
∆UAB = QAB = nCV∆T
TBA
T
TB
Q
Termostato
V = cost
A
C
TC = TB
V
Per un gas perfetto ∆U = nCV∆T , per tutte le trasformazioni.
L’energia interna U è una funzione di stato: il suo valore dipende solo
dallo stato in cui si trova il sistema e la sua variazione dipende solo
dallo stato iniziale e dallo stato finale e non dalla trasformazione.
∆U AC = ∆U AB + ∆U BC = ∆U AB = nCV ∆T
Università Politecnica delle Marche, Facoltà di Agraria
C.d.L. Scienze Forestali e Ambientali, A.A. 2010/2011, Fisica
Trasformazione isocora:
P
V = costante; P/T = costante
B
LAB = 0
∆UAB = QAB = nCV∆T
A
V
Trasformazione isobara:
P = costante; V/T = costante
P
∆UAB = nCV∆T
A
B
LAB = P∆V = nR∆T
QAB = ∆UAB + LAB = nCV∆T+nR∆T =
V
= nCP∆T
Università Politecnica delle Marche, Facoltà di Agraria
C.d.L. Scienze Forestali e Ambientali, A.A. 2010/2011, Fisica
Trasformazione isotermica:
p
∆U = nCV∆T = 0
L = ∑i pi ∆V i
p
A
PV = nRT
A
∆Vi→0
nRT
pi =
Vi
B
B
V
∆Vi
L = nRT ∑ i
L = nRTln
L = lim ∑ i pi ∆V i
∆V i
Vi
V fi n
Vin
V
L = nRT ⋅ lim ∑ i
∆V →0
pin
L = nRTln
p fin
∆V i
Vi
Q = L = nRTln
V fi n
Vin
Università Politecnica delle Marche, Facoltà di Agraria
C.d.L. Scienze Forestali e Ambientali, A.A. 2010/2011, Fisica
Trasformazione adiabatica:
p
L = - ∆U = - nCV∆T
Q=0
A
γ
PV = cos t
B
TA
TB
V
nRT
PV = nRT ⇒ P =
V
⇒ TV
γ −1
= cos t
Università Politecnica delle Marche, Facoltà di Agraria
C.d.L. Scienze Forestali e Ambientali, A.A. 2010/2011, Fisica
Esercizio:
Una mole di gas biatomico si trova a temperatura TA e
volume VA. Dal punto iniziale A, il gas subisce una
espansione isotermica fino a un volume VB = 3 VA e poi
una compressione adiabatica fino a PC = PA.
Determinare:
a) PC, VC, TC;
b) LAC;
c) QAC.
Università Politecnica delle Marche, Facoltà di Agraria
C.d.L. Scienze Forestali e Ambientali, A.A. 2010/2011, Fisica
L’entropia:
TB
TA
interazione termica
freddo caldo
equilibrio termico
- non c’è variazione dell’energia totale del sistema;
- il calore assorbito fa variare la sua energia interna ma anche il suo
livello di disordine;
L’entropia (S) di un sistema rappresenta una misura
quantitativa del suo disordine.
L’entropia è una grandezza di stato.
Università Politecnica delle Marche, Facoltà di Agraria
C.d.L. Scienze Forestali e Ambientali, A.A. 2010/2011, Fisica
Q
∆S =
T
[S ]SI
J
=
K
- calore assorbito fa aumentare l’entropia;
- calore ceduto fa diminuire l’entropia;
∆ S tot
−Q Q
= ∆S A + ∆S B =
+
TA
TB
T A f TB
⇒
Q
Q
p
TA
TB
⇒
∆ S tot f 0
Università Politecnica delle Marche, Facoltà di Agraria
C.d.L. Scienze Forestali e Ambientali, A.A. 2010/2011, Fisica
p
Trasformazione isotermica:
A
Q = L = nRT ln
V fin
Vin
B
V
∆S = nR ln
V fin
Vin
VFin
nRT ln
V fin
Vin
Q
∆S = =
= nR ln
T
T
Vin
Pin
= nR ln
Pfin
Università Politecnica delle Marche, Facoltà di Agraria
C.d.L. Scienze Forestali e Ambientali, A.A. 2010/2011, Fisica
p
Trasformazione isocora:
B
∆UAB = QAB = n CV ∆T
A
V
n
∆S isoc
n
n
Qi
nCV ∆Ti
∆Ti
=∑
=
nC
=∑
V∑
T
T
i =1 Ti
i =1 i
i =1
i
e al limite per ∆Ti tendente a zero:
Pfin
T fin
∆Ti
= nCV ln
= nCV lim ∑
= nCV ln
∆Ti → 0
Pin
Tin
i =1 Ti
n
∆S isoc
Università Politecnica delle Marche, Facoltà di Agraria
C.d.L. Scienze Forestali e Ambientali, A.A. 2010/2011, Fisica
Trasformazione isobara:
p
A
QAB = n CP ∆T
B
V
n
∆S isob
n
n
Qi
nC P ∆Ti
∆Ti
=∑
=∑
= nC P ∑
Ti
i =1 Ti
i =1
i =1 Ti
e al limite per ∆Ti tendente a zero:
V fin
T fin
∆Ti
= nC P lim ∑
= nC P ln
= nC P ln
∆Ti → 0
Tin
i =1 Ti
Vin
n
∆S isob
Università Politecnica delle Marche, Facoltà di Agraria
C.d.L. Scienze Forestali e Ambientali, A.A. 2010/2011, Fisica
Trasformazione adiabatica: Q = 0
Trasformazione qualsiasi:
P
∆S = 0
S - grandezza di stato
A
C
=>
∆S AB = ∆S AC + ∆SCB
TC
TB
= nCV ln
+ nC P ln
TA
TC
∆S AB
pC
VB
= nCV ln
+ nC P ln
pA
VC
∆S AB
pB
VB
= nCV ln
+ nC P ln
pA
VA
B
V
Università Politecnica delle Marche, Facoltà di Agraria
C.d.L. Scienze Forestali e Ambientali, A.A. 2010/2011, Fisica
Il grafico delle trasformazioni termodinamiche nel piano T – S :
Q = T ∆S
T
T
B
A
B
A
trasformazione
isoterma
Q
trasformazione
isobara
Q
S
T
S
T
B
A
trasformazione
isocora
Q
S
trasformazione
adiabatica
B
A
S
Università Politecnica delle Marche, Facoltà di Agraria
C.d.L. Scienze Forestali e Ambientali, A.A. 2010/2011, Fisica
Riscaldamento o raffreddamento di un solido o di un liquido
Dividiamo la trasformazione in tante microtrasformazioni
durante le quali la temperatura possa essere ritenuta
costante.
n
n
n
Qi
mc∆Ti
∆Ti
∆S = ∑
=∑
= mc ∑
Ti
i =1 Ti
i =1
i =1 Ti
e al limite per ∆Ti tendente a zero:
T fin
∆Ti
∆S = mc lim ∑
= mc ln
∆Ti → 0
Tin
i =1 Ti
n
Università Politecnica delle Marche, Facoltà di Agraria
C.d.L. Scienze Forestali e Ambientali, A.A. 2010/2011, Fisica
Cambiamenti di fase:
Avvengono a temperatura costante e sono caratterizzati da un
calore latente L dato in genere in J/kg o calorie per grammo.
Q mL
∆S = =
T
T
Ad esempio il calore latente di fusione del ghiaccio è LF = 80
cal/g.
La variazione di entropia relativa alla fusione di 1 kg di ghiaccio
vale:
Q mLF 10 3 ⋅ 80 ⋅ 4.186
∆S = =
=
= 1227 JK -1
T
T
273
Università Politecnica delle Marche, Facoltà di Agraria
C.d.L. Scienze Forestali e Ambientali, A.A. 2010/2011, Fisica
Entropia crescente
Solido
∆S > 0
∆S > 0
∆S < 0
∆S < 0
Liquido
S(solido) < S(liquido) <
Gas
S(Gas)
Università Politecnica delle Marche, Facoltà di Agraria
C.d.L. Scienze Forestali e Ambientali, A.A. 2010/2011, Fisica
Per l’esercizio precedente determinare:
d) ∆SAC