STATISTICA ED EPIDEMIOLOGIA

Università degli Studi di Padova
Corso di Laurea in Medicina e Chirurgia - A.A. 2015-16
Corso Integrato: Statistica e Metodologia Epidemiologica
Disciplina: Statistica e Metodologia Epidemiologica 2
Docenti: prof.ssa Anna Chiara FRIGO – prof.ssa Egle PERISSINOTTO
Modulo 6: Relazione tra variabili quantitative
•
Il modello di regressione lineare semplice
•
I coefficienti di regressione e correlazione
•
Il coefficiente di correlazione per ranghi di Spearman
•
Il coefficiente di determinazione
•
Verifica di ipotesi sui coefficienti di regressione e correlazione
RELAZIONE TRA VARIABILI QUANTITATIVE
Quando si prendono in considerazione
congiuntamente due o più variabili quantitative
oltre alle analisi descrittive sulla loro media e
varianza, è possibile esaminare anche il tipo e
l'intensità delle relazioni che sussistono tra
loro.
Per esempio, quando per ogni individuo si
misurano contemporaneamente peso e statura, è
possibile verificare statisticamente se queste due
variabili cambiano simultaneamente, valutando
direzione ed intensità della loro relazione.
REGRESSIONE E CORRELAZIONE (1)
1.
2.
Quale relazione matematica (con segno ed
intensità) esiste tra peso e statura?
La tendenza calcolata è significativa, presente
anche nella popolazione, oppure solo apparente,
effetto probabile di variazioni casuali del
campione?
Per rispondere a queste domande, nel caso della
rilevazione congiunta di due variabili, è possibile
ricorrere:
1. all'analisi della regressione,
2. all’analisi della correlazione,
tra loro concettualmente alternative, ma fondate su
principi e metodi simili.
REGRESSIONE E CORRELAZIONE (2)
Si ricorre all'analisi della regressione quando dai dati
campionari si vuole ricavare un modello statistico che
predica i valori di una variabile (Y) detta dipendente o
risposta, individuata come effetto, a partire dai valori
dell'altra variabile (X), detta indipendente o
esplicativa.
Si ricorre all'analisi della correlazione quando si vuole
misurare l'intensità dell'associazione tra due variabili
quantitative (X1 e X2) che variano congiuntamente,
senza che tra esse esista una relazione diretta di
causa-effetto.
Ciò può avvenire quando entrambe sono legate a una
terza variabile, o perché hanno un’evoluzione temporale
simile o una differenziazione spaziale analoga.
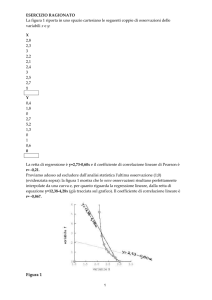
PROBLEMA
Supponiamo di voler verificare se tra peso (Y) e statura (X)
possa sussistere una relazione di tipo lineare.
Consideriamo quindi un campione di n coppie di valori per le
due variabili xi e yi (i =1, 2, …, n).
La costruzione di un grafico per i dati campionari (o di
trasformazioni di essi) su un diagramma bidimensionale per
punti ci permetterà di verificare se è possibile specificare
una forma funzionale lineare.
120
Peso (Kg)
110
100
90
80
70
60
160 165 170 175 180 185 190 195 200
Statura (cm)
IL MODELLO DI REGRESSIONE LINEARE
SEMPLICE
La relazione matematica più semplice che si può
ipotizzare tra due variabili quantitative (X variabile
indipendente e Y variabile dipendente) è la
regressione
lineare
semplice,
rappresentata
dall’equazione:
Y    X
dove:
•  rappresenta l'intercetta della retta di regressione,
•  è il coefficiente angolare della retta di regressione e
indica di quanto varia in media Y al variare di una
unità di X
… ritorniamo al nostro PROBLEMA
Dai dati campionari dobbiamo stimare i parametri incogniti  e 
della retta specificata.
Se la relazione lineare postulata valesse con esattezza, non vi
sarebbe bisogno di stimare i parametri in quanto presi due punti
campionari, si potrebbe tracciare la retta e tutti i punti restanti
giacerebbero proprio lungo la retta tracciata.
120
Peso (Kg)
110
100
90
80
70
60
160 165 170 175 180 185 190 195 200
Statura (cm)
Le relazioni funzionali esatte non descrivono adeguatamente
comportamenti biologici, sociali, economici, ecc..
Per questo motivo i punti non sono allineati sulla retta ma dispersi
attorno alla retta.
IL METODO DEI MINIMI QUADRATI
Una qualsiasi retta Ŷ  a  bX
tracciata attraverso i
punti di un diagramma di dispersione è una stima della
relazione ipotizzata:
Y    X  


I residui sono dati da: i  Yi  Ŷi  Yi  a  bXi , i  1, ..., n
Con il principio dei minimi quadrati si determinano a e b
(stime di  e ) in modo da minimizzare:
i
n
n
    Yi  a  bXi 
i1
2
i
i1
2
GLI STIMATORI DEI MINIMI QUADRATI
Si dimostra che i valori dei parametri a e b che
minimizzano la precedente relazione sono:
n
 Y  M X  M 
n
b
 Y  M X  M 
i1
i
n
Y
i
X
 X i  M X 
i1
2
i1

i
Y
n
n
2


X

M
 i X
i1
n
a  MY  bMX
i
X

cov( X, Y )
var( X)
PROPRIETÀ DELLA RETTA DI
REGRESSIONE
• La retta passa sempre per il punto medio di coordinate (Mx ; My);
• a rappresenta l’intercetta tra la retta di regressione e l’asse delle
ordinate;
• b rappresenta l’incremento (o decremento) medio della variabile
dipendente ad una variazione unitaria della variabile
indipendente;
• b può assumere qualsiasi valore positivo e negativo:
– se assume
indipendente
concorde),
– se assume
indipendente
discorde).
un valore positivo, all’aumentare della variabile
anche la variabile dipendente aumenta (variazione
valore negativo, all’aumentare della variabile
la variabile dipendente diminuisce (variazione
ESEMPIO: stima dei parametri della retta di
regressione (1)
La tabella seguente riporta i risultati di un test di ammissione ad un
corso di laurea ed il voto medio degli esami del primo anno in un
gruppo di sette studenti.
RISULTATO
TEST DI
AMMISSIONE
X
VOTO MEDIO
ESAMI PRIMO
ANNO
Y
1
13
25
2
11
24
3
15
28
4
10
20
5
10
21
6
14
27
7
11
23
Relazione tra risultato al test di ammissione e
voto medio esami primo anno
VOTO MEDIO ESAMI
PRIMO ANNO (Y)
STUDENTE
30
29
28
27
26
25
24
23
22
21
20
19
18
9
10
11
12
13
14
RISULTATO TEST DI AMMISSIONE (X)
15
16
ESEMPIO: stima dei parametri della retta di
regressione (2)
MX 
RISULTATO
TEST DI
AMMISSIONE
X
VOTO MEDIO ESAMI
PRIMO ANNO
Y
(X-MX)
(Y-MY)
(X-MX)(Y-MY)
(X-MX)²
(Y-MY)²
1
13
25
1
1
1
1
1
2
11
24
-1
0
0
1
0
3
15
28
3
4
12
9
16
4
10
20
-2
-4
8
4
16
5
10
21
-2
-3
6
4
9
6
14
27
2
3
6
4
9
7
11
23
-1
-1
1
1
1

84
168
0
0
34
24
52
84
 12
7
MY 
168
 24
7
n
b
 Y  M X  M 
i1
i
Y
i
n
2


X

M
 i X
i1
a  24  1,42  12  7
X
34

 1,42
24
Relazione tra risultato al test di ammissione e
voto medio esami primo anno
VOTO MEDIO ESAMI
PRIMO ANNO (Y)
STUDENTE
30
29
28
27
26
25
24
23
22
21
20
19
18
y = 1,42 x + 7
(MX, MY)
9
10
11
12
13
14
RISULTATO TEST DI AMMISSIONE (X)
15
16
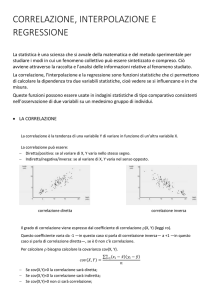
LA CORRELAZIONE LINEARE
• Misura la strettezza del legame (supposto
lineare) tra due variabili quantitative
• È simmetrica, stessa di correlazione di Y/X e di
X/Y
• Indici:
– , coefficiente di correlazione di Pearson
–  ², indice di determinazione lineare
IL COEFFICIENTE DI CORRELAZIONE
La stima del coefficiente di correlazione di Pearson è
definita come:
cov( X, Y) cov( X, Y)  s x
sx
rxy 

 b
sx sy
var(X)  s y
sy
 1 r   1
da cui si deduce la relazione tra coefficiente di
correlazione e coefficiente di regressione
Esso misura la strettezza e la direzione del legame
lineare tra due variabili
ESEMPI DI VALORI DEL COEFFICIENTE DI
CORRELAZIONE
IL COEFFICIENTE DI CORRELAZIONE PER
RANGHI
Cograduazione
Intensità della relazione tra due caratteri espressi su
scala ordinale.
Le unità vengono ordinate per valori crescenti
distintamente per X e Y, e caratterizzate per il rango
(posto d’ordine) di X e Y.
Per la generica unità i-esima, si considera la differenza
di tra i suoi due ranghi.
Indice di cograduazione di Spearman:
n
rs  1 
6   di2
i 1
2
n  n  1
 1  rs   1
ESEMPIO: indice di cograduazione di Spearman
STUDENTE
RISULTATO
TEST DI
AMMISSIONE
X
VOTO MEDIO
ESAMI PRIMO
ANNO
Y
RANGO DI
X
RANGO DI
Y
DIFFERENZA
TRA
GRADUATORIE
dI
1
13
25
5
5
0,0
0,00
2
11
24
3,5
4
-0,5
0,25
3
15
28
7
7
0,0
0,00
4
10
20
1,5
1
0,5
0,25
5
10
21
1,5
2
-0,5
0,25
6
14
27
6
6
0,0
0,00
7
11
23
3,5
3
0,5
0,25

rs  1 
6 1
 0,98
7  49  1
dI ²
1
CORRELAZIONE E INDIPENDENZA
Il coefficiente di correlazione dà un’idea di quanto le osservazioni congiunte
di due variabili siano tendenzialmente allineate lungo una retta.
Se due variabili sono INDIPENDENTI tra di loro la CORRELAZIONE
(lineare) sarà nulla (e quindi r = 0).
PERÒ NON è vero il contrario
Se il coefficiente di correlazione lineare è nullo, o quasi, non è detto che tra
le due variabili ci sia indipendenza.
Ad esempio:
X 10 15 16 59,3 58,2 45,9 51 63 35,6 26
Y 70 41 55 38 50 27 35 82 18 28
Il coefficiente di correlazione è r = 0,012
(devianza di x = 3664,9, codevianza = 45,5)
Quindi si può dire che non c’è una relazione lineare tra X e Y, ma
graficamente... si vede una relazione anche se non di tipo lineare.
CORRELAZIONE E CAUSALITÀ
ATTENZIONE: CORRELAZIONE NON
IMPLICA CAUSALITÀ!
Esempio
Dopo una festa, dove vengono serviti vino e
noccioline, alcune delle persone si
ammalano. Un medico intervista le persone
ammalate e valuta il livello dei sintomi, il
consumo di vino e quello di noccioline.
Il medico trova che più vino le persone
hanno bevuto più sono gravi i sintomi: cioè
vino e sintomi sono correlati.
r = 0,68 (p ≤ 0,05)
Questo porterebbe a pensare che sia stato
il vino a causare la malattia.
In realtà la causa sono le noccioline, le
persone ammalate hanno mangiato più
noccioline delle altre e di conseguenza
hanno bevuto più vino!
IL COEFFICIENTE DI DETERMINAZIONE
LINEARE
Si ha che:
cov 2 (X, Y)
var(X) var(Y)  var(ε)
2
2
R r 

b


0

r
1
2 2
sxsy
var(Y)
var(Y)
2
2
misura la frazione di varianza (variabilità) totale
spiegata dalla regressione, cioè misura la capacità
predittiva del modello lineare costruito sui dati empirici.
Il coefficiente di determinazione misura quanto bene la
retta di regressione rappresenta i dati, quindi se la retta
passasse esattamente attraverso tutti i punti del
diagramma di dispersione, sarebbe capace di spiegare
tutta la variabilità.
ESEMPI DI VALORI DEL COEFFICIENTE DI
DETERMINAZIONE LINEARE
ESEMPIO: calcolo del coefficiente di correlazione
e di determinazione
STUDENTE
RISULTATO
TEST DI
AMMISSIONE
X
VOTO MEDIO ESAMI
PRIMO ANNO
Y
1
13
2
(X-MX)
(Y-MY)
(X-MX)(Y-MY)
(X-MX)²
(Y-MY)²
25
1
1
1
1
1
11
24
-1
0
0
1
0
3
15
28
3
4
12
9
16
4
10
20
-2
-4
8
4
16
5
10
21
-2
-3
6
4
9
6
14
27
2
3
6
4
9
7
11
23
-1
-1
1
1
1

84
168
0
0
34
24
52
Relazione tra risultato al test di ammissione e
voto medio esami primo anno
r
 Y  M X  M 
i
Y
i
X
i1
2
2
 Xi  MX    Yi  My 
n
n
i1
i1
r 2  0,92

34
 0,96
24  52
VOTO MEDIO ESAMI
PRIMO ANNO (Y)
n
30
29
28
27
26
25
24
23
22
21
20
19
18
y = 1,42 x + 7
9
10
11
12
13
14
RISULTATO TEST DI AMMISSIONE (X)
15
16
DISTRIBUZIONE DI b (1)
Si supponga che siano oggetto di studio due variabili (X,Y) e che
dalla popolazione di riferimento vengano estratti 10.000 campioni
composti da 5 coppie di valori (x,y). L’applicazione del principio dei
minimi quadrati dà luogo a 10.000 coppie di stime a e b.
Tali valori potrebbero essere classificati secondo una distribuzione
di frequenza bivariata e, al crescere indefinito del numero di
campioni, tale distribuzione tenderebbe ad una funzione continua
detta distribuzione campionaria congiunta.
Da tale distribuzione congiunta potremmo ricavare le distribuzioni
marginali (consideriamo solo lo stimatore di ) e le caratteristiche
fondamentali per la valutazione di uno stimatore:
Mb  
2
var( b)   
2


X

M

x
2
b
INFERENZA SU 
• Intervallo di fiducia di livello (1-) per 
b  t (n2), 2  s
2


X

M

X
• Verifica di ipotesi
H0: = 0
H1:  0
funzione test:
b  0
t
s
 X  M 
2
X
 t n2
ESEMPIO: verifica di ipotesi sul coefficiente di
regressione
STUDENTE
RISULTATO
TEST DI
AMMISSIONE
X
VOTO MEDIO
ESAMI PRIMO
ANNO
Y
1
13
2
(X-MX)²
Y^ = 7+1,42X
(Y-Y^)
(Y-Y^)²
25
1
25,46
-0,46
0,2116
11
24
1
22,62
1,38
1,9044
3
15
28
9
28,30
-0,30
0,0900
4
10
20
4
21,20
-1,2
1,4400
5
10
21
4
21,20
-0,20
0,0400
6
14
27
4
26,88
0,12
0,0144
7
11
23
1
22,62
0,38
0,1444

84
168
24
3,8448
Relazione tra risultato al test di ammissione e
voto medio esami primo anno
1,42  1,00
t
 2,34
0,88 / 24
t 5; 0,025  2,5706
IC95% = (1,42  2,57010,88/24) =
= (0,96; 1,88)
VOTO MEDIO ESAMI
PRIMO ANNO (Y)
H0: = 1
H1:  1
30
29
28
27
26
25
24
23
22
21
20
19
18
y = 1,42 x + 7
9
10
11
12
13
14
RISULTATO TEST DI AMMISSIONE (X)
15
16
INFERENZA SU 
• La verifica di ipotesi:
H0:  = 0
H1:   0
equivale a:
H0:  = 0
H1:   0
dove  è la correlazione nella popolazione.
La funzione test risulta quindi:
t
r
1 r  n  2
2
r
n2
 t n2
2
1 r
ESEMPIO: verifica di ipotesi sul coefficiente di
correlazione
STUDENTE
RISULTATO
TEST DI
AMMISSIONE
X
VOTO MEDIO
ESAMI PRIMO
ANNO
Y
1
13
2
(X-MX)²
Y^ = 7+1,42X
(Y-Y^)
(Y-Y^)²
25
1
25,46
-0,46
0,2116
11
24
1
22,62
1,38
1,9044
3
15
28
9
28,30
-0,30
0,0900
4
10
20
4
21,20
-1,2
1,4400
5
10
21
4
21,20
-0,20
0,0400
6
14
27
4
26,88
0,12
0,0144
7
11
23
1
22,62
0,38
0,1444

84
168
24
t  0,96
→
72
 7,59
1  0,92
t 5; 0,025  2,5706
H0:  = 0
H0:   0
t
1,42
 7,91
0,88 24
Relazione tra risultato al test di ammissione e
voto medio esami primo anno
VOTO MEDIO ESAMI PRIMO
ANNO (Y)
H0:  = 0
H0:   0
3,8448
30
29
28
27
26
25
24
23
22
21
20
19
18
y = 1,42 x + 7
9
10
11
12
13
14
RISULTATO TEST DI AMMISSIONE (X)
15
16