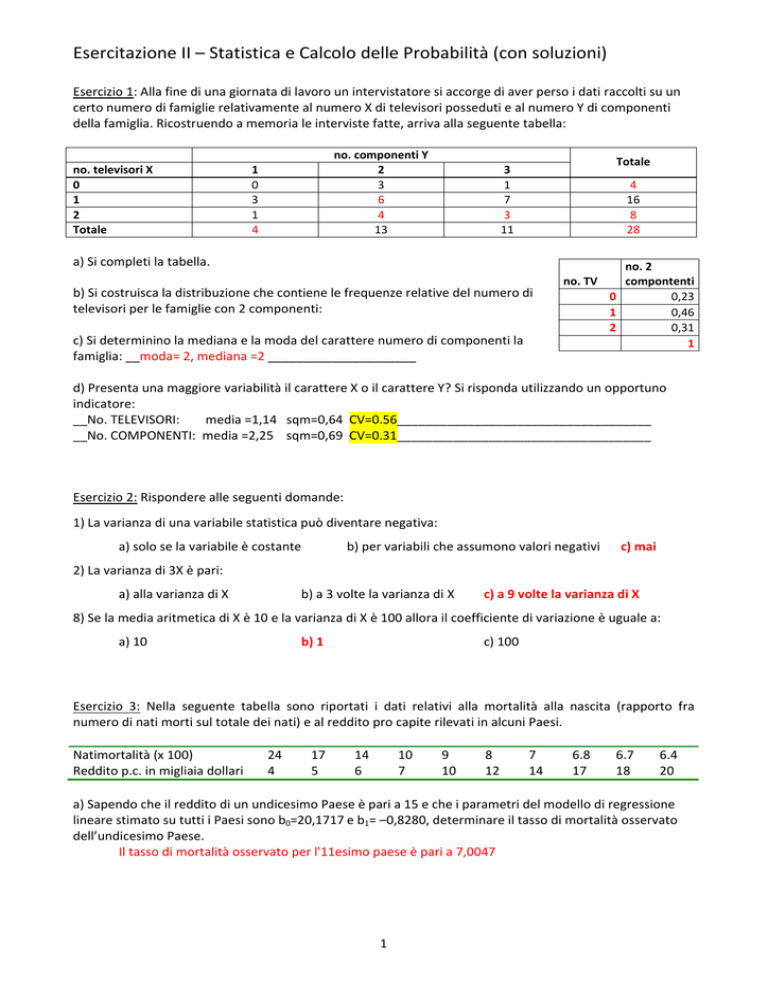
Esercitazione II – Statistica e Calcolo delle Probabilità (con soluzioni) Esercizio 1: Alla fine di una giornata di lavoro un intervistatore si accorge di aver perso i dati raccolti su un certo numero di famiglie relativamente al numero X di televisori posseduti e al numero Y di componenti della famiglia. Ricostruendo a memoria le interviste fatte, arriva alla seguente tabella: no. televisori X 0 1 2 Totale no. componenti Y 2 3 6 4 13 1 0 3 1 4 3 1 7 3 11 Totale 4 16 8 28 a) Si completi la tabella. no. 2 no. TV compontenti
b) Si costruisca la distribuzione che contiene le frequenze relative del numero di 0 0,23
televisori per le famiglie con 2 componenti: 1 0,46
2 0,31
c) Si determinino la mediana e la moda del carattere numero di componenti la 1
famiglia: __moda= 2, mediana =2 _____________________ d) Presenta una maggiore variabilità il carattere X o il carattere Y? Si risponda utilizzando un opportuno indicatore: __No. TELEVISORI: media =1,14 sqm=0,64 CV=0.56____________________________________ __No. COMPONENTI: media =2,25 sqm=0,69 CV=0.31____________________________________ Esercizio 2: Rispondere alle seguenti domande: 1) La varianza di una variabile statistica può diventare negativa: a) solo se la variabile è costante b) per variabili che assumono valori negativi c) mai 2) La varianza di 3X è pari: a) alla varianza di X b) a 3 volte la varianza di X c) a 9 volte la varianza di X 8) Se la media aritmetica di X è 10 e la varianza di X è 100 allora il coefficiente di variazione è uguale a: a) 10 b) 1 c) 100 Esercizio 3: Nella seguente tabella sono riportati i dati relativi alla mortalità alla nascita (rapporto fra numero di nati morti sul totale dei nati) e al reddito pro capite rilevati in alcuni Paesi. Natimortalità (x 100) 24 17 14 10 9 8 7 6.8 6.7 6.4 Reddito p.c. in migliaia dollari 4 5 6 7 10 12 14 17 18 20 a) Sapendo che il reddito di un undicesimo Paese è pari a 15 e che i parametri del modello di regressione lineare stimato su tutti i Paesi sono b0=20,1717 e b1= –0,8280, determinare il tasso di mortalità osservato dell’undicesimo Paese. Il tasso di mortalità osservato per l'11esimo paese è pari a 7,0047 1 Esercizio 4: Nella seguente tabella sono riportati le ore di studio e il voto all'esame di statistica: Ore di studio 30 33 35 40 45 52 58 Voto 18 21 23 25 27 28 29 a) Di quanto varia in media il voto all'aumentare di un'ora di studio? b0=9.23, b1=0.36 b) Quante ore devo studiare in più se voglio migliorare in media di due punti il mio voto? Devo aumentare di 5,51 ore. c) Quanto vale la correlazione fra ore di studio e voto? La correlazione r vale 0.94 d) Come cambierebbe la misura di correlazione se anziché misurare il tempo in ore misurassi il tempo in minuti? Non cambierebbe. Esercizio 5: • Trovare l'equazione della retta di regressione per prevedere il punteggio all'esame finale, sulla base di quello ottenuto in un esame parziale. I dati sono: parziale: punteggio medio=70, scarto quadratico medio=10 finale: punteggio medio=55, scarto quadratico medio=20 Coefficiente di correlazione lineare r=0.6 b1=r Sy/Sx=0.6*20/10=1.2 b0=y.medio‐b1*x.medio=55‐1.2*70= ‐29 • Quale voto si aspetta di prendere all'esame finale uno che abbia conseguito 80 all'esame parziale? y*=‐29+1.2*80=67 • Quanto vale la devianza di dispersione per il modello considerato? Non si può determinare perché non si ha a disposizione nessuna informazione su n. • Se i voti anziché essere espressi in centesimi fossero espressi in 30 come varierebbe il coefficiente di regressione? In questo caso il coefficiente di regressione non cambia. Esercizio 6: Alcuni ricercatori hanno studiato i dati relativi alle immatricolazioni presso una certa facoltà: ogni studente deve riempire un questionario con i suoi dati anagrafici e quelli della sua famiglia. • Il coefficiente di correlazione tra l'età dello studente e il suo anno di nascita è: ‐1 circa ‐1 un valore negativo 0 un valore positivo circa 1 1 • Il coefficiente di correlazione tra l'età dello studente e quello della madre è: ‐1 circa ‐1 un valore negativo 0 un valore positivo circa 1 1 Esercizio 7: E' stato effettuato un sondaggio per esplorare l'atteggiamento dei residenti in una città nei confronti della chiusura totale al traffico di alcune vie del centro storico. La tabella seguente riporta la classificazione dei 654 rispondenti secondo i due caratteri 'fascia d'età' e 'tipo di atteggiamento': Contrario Incerto Favorevole 16 ‐| 25 20 24 180 25 ‐| 40 26 36 123 40 ‐| 65 80 30 15 65 ‐| 85 90 20 10 a) Qual è la percentuale di persone che si sono dichiarate favorevoli e hanno più di 65 anni? 10/654*100=1.53% b) Qual è la percentuale di contrari fra i giovani (16 ‐| 25 anni)? 20/224*100=8.93% 2 c) Il tipo di atteggiamento è indipendente in distribuzione dall'età? Rispondere utilizzando l'indicatore più adeguato e commentare il risultato No, Tchuprov=0.43141 Esercizio 8: Si consideri la distribuzione percentuale, secondo il voto riportato all'esame di maturità e il sesso per gli studenti iscritti ai corsi di laurea in Matematica nell'a.a. 2004‐05: Sesso/Voto 60‐69 70‐79 80‐89 90‐100 F 9.5 16.9 17.9 55.7 100 M 22.5 19.6 18.5 39.4 100 15.8 18.2 18.0 48.0 100 a) Si completi la distribuzione b) Sapendo che le femmine sono 866 e i maschi 799 si calcoli l'indicatore χ2 : 69.24 (T di Tchuprov =0,155) c) Si calcoli il voto medio dei maschi : 82.177 d) Il voto dipende in media dal sesso? Si risponda utilizzando un opportuno indicatore: η2=0,039 Esercizio 9: Uno studio condotto su 1000 famiglie ha dato luogo ai seguenti risultati: Statura media del marito=173 cm scarto quadratico medio=7cm Statura media della moglie=160 cm scarto quadratico medio=6cm Coefficiente di correlazione lineare r=0.45 a) Si determinino l'intercetta e il coefficiente di regressione della retta di regressione riferita alle variabili in oggetto in cui la statura del marito è assunta quale variabile indipendente: b1=r Sy/Sx=0.45*6/7=0.386 b0=y.medio‐b1*x.medio=160‐0.386*173=93.222 b) Si preveda la statura della moglie il cui marito è alto 183cm y*=93.222+0.386*183=163.86 Esercizio 10: Il proprietario di una ditta di consegna di nafta per riscaldamento effettua un'indagine circa la rapidità con la quale vengono saldate le fatture in tre diverse zone periferiche. Estrae a tal fine da ognuna delle tre zone un campione di 100 conti, registrando il numero di giorni intercorrenti tra la consegna della nafta e il saldo della fattura. I risultati sono riportati nella tabella che segue: Zona I Zona II Zona III Da 1 a 15 giorni 34 42 40 Da 16 a 30 giorni 48 50 46 Più di 30 giorni 18 8 14 100 100 100 Valutare, con un opportuno indicatore, se il numero di giorni necessari per saldare le fatture dipende in distribuzione dalla zona periferica. Tchuprov=0.09003 Esercizio 11: Fra due variabili X e Y esiste la relazione lineare calcolata con il metodo dei minimi quadrati: Y=13.05‐0.80X. Conoscendo solo le seguenti informazioni X 5 3 6 4 4 Residui 2.9 0.3 ‐1.3 ‐1.9 0 a) Inserire il valore mancante nella tabella 3 b) Calcolare i valori osservati della variabile Y: y.oss 11,95 10,95
6,95
7,95 9,85
Esercizio 12: Un virus informatico ha cancellato alcuni dati relativi ad un’analisi di regressione lineare semplice effettuata su un campione di 24 osservazioni. I dati ancora leggibili sono i seguenti: media di X = 5, media di Y= 10, varianze di X = 100 e di Y = 49, intercetta = 11.7 ottenuta con il metodo dei minimi quadrati. a) si ricavi il coefficiente di regressione lineare: b1=‐0.34 b) si ricavi R2, l’indice di determinazione lineare del modello: R2=0.24 c) se una unità statistica presenta un valore della variabile indipendente X pari a 5 quale sarà il corrispondente valore y* sulla retta di regressione: y*=10, è il baricentro Esercizio 13: In uno studio volto a studiare la relazione tra la distanza tra due città e la corrispondente tariffa aerea si sono rilevate le distanze tra Baltimora e 12 diverse città americane (in miglia) e il costo dei relativi biglietti aerei per viaggi di sola andata (in dollari). Si sono ottenuti i seguenti valori Distanza media = 712,7 Costo medio del biglietto = 166,9 Scarto quadratico medio della distanza = 402,7 Scarto quadratico medio del costo del biglietto=59,5 Coefficiente di correlazione lineare = 0,795 a) si ricavi il coefficiente di regressione lineare del modello di regressione che assume il costo del biglietto come variabile dipendente e la distanza come variabile indipendente: b1=0.117463 b) si ricavi la devianza di regressione: DevRegr=26850.32 c) se una unità città dista da Baltimora 576 miglia quale sarà il corrispondente costo del biglietto y* ? y*=150.8428 Esercizio 14: Si vuole studiare la relazione tra la durata di un messaggio pubblicitario televisivo e il tempo di ricordo dello stesso. Durante un programma televisivo di 1 ora vengono mostrati a 60 individui messaggi pubblicitari di durata diversa relativi allo stesso dentifricio. Ogni individuo viene poi sottoposto a un test volto a misurare la quantità di caratteristiche del prodotto che ricorda. Si ottengono i seguenti risultati: Durata media del messaggio pubblicitario = 38 secondi Codevianza fra durata e punteggio = 3060 Coefficiente di correlazione lineare = 0,538 Punteggio medio nel test di memoria = 13,8 Devianza del punteggio = 28296 a) si ricavi la devianza della variabile durata del messaggio pubblicitario: Dev(dur.)=1143.28 b) si ricavi il coefficiente di regressione lineare del modello di regressione che assume il punteggio del test di memoria come variabile dipendente e la durata del messaggio come variabile indipendente: b1=2.68 c) Se la somma dei residui y‐y* relativi ai primi 59 individui è 3, quanto vale il residuo relativo all’ultima unità statistica?: y60‐y*60=‐3
Esercizio 15: Si consideri la seguente distribuzione di 211 diplomati secondo la classe di reddito delle famiglie (in migliaia di euro) 4 Classi Frequenze relative 0 |‐ 15 15 |‐ 25 25 |‐ 50 50 |– 100 0.12 0.33 0.4 0.15 a)
b)
c)
d)
e)
Completare la tabella______ Si determini il numero di studenti con reddito inferiore ai 25.000 euro____ 95 Calcolare il reddito medio___33.75 Calcolare la classe modale___15 |‐ 25 Sapendo che in due successive indagini su due gruppi di 150 e 203 studenti il reddito medio è risultato pari a 35.000 e 29.000 euro rispettivamente, determinare il reddito medio del collettivo totale ___31549.48 Esercizio 16: La seguente tabella esprime i tempi di durata (in ore) di un certo numero di apparecchiature elettroniche. Durata Frequenze 0 |‐ 100 100 |‐ 200 200 |‐ 400 400 |– 700 700 |‐ 900 80 48 48 19 5 a) Considerando che la percentuale di apparecchiature elettroniche con durata 100 |‐ 200 è il 24%, completare la tabella____ b) Si determini la percentuale di apparecchiature con durata superiore alle 400 ore.__12%____ c) Calcolare il tempo medio___200.25 d) Calcolare la classe modale__0|‐100 e) Immaginando che queste apparecchiature vengano migliorate in modo da aumentarne la durata media di 5 ore, calcolare la nuova durata media in minuti.___205.25h, 12315 minuti 5












