La legge di Ampére
Consideriamo un filo infinito percorso da corrente
La corrente produce in A un campo magnetico
⊥ al filo e ad r
r µ0 i r
B=
uθ
i
2
π
r
B
O r
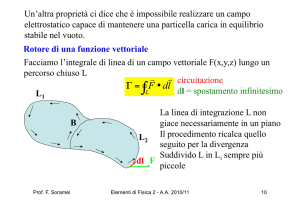
Ci chiediamo ora quanto valga la circuitazione di B
A
r r
Λ B = ∫ B •dl = ?
Consideriamo la circonferenza di raggio r concentrica con il filo e ⊥ ad
esso. B è sempre tangente alla circonferenza ⇒ B·dl = Bdl, inoltre sulla
circonferenza B è costante, quindi
r r
µ0 i
∫L B • dl = ∫L Bdl = B ∫L dl = B 2πr = 2πr 2πr = µ0i
Prof. F. Soramel
Fisica Generale II A.A. 2003/04
1
La circuitazione di B non dipende dal raggio, ma solo dal fatto che la
circonferenza racchiuda il filo percorso da corrente (concatenata).
Consideriamo ora un percorso generico concatenato con la corrente
L
i
dθ b
r
a dl
B
uθ
r
r
r r µ 0 i urθ • dl r
∫L B • dl = 2π ∫L r uθ • dl = rdθ componente dl direzione di θ
r r µ0i
µ 0i
B
•
d
l
=
d
θ
=
2π = µ 0i
∫L
2π ∫L
2π
Otteniamo dunque che la circuitazione di B in condizioni statiche vale
sempre µ 0i (legge di Ampére) con i = Σ correnti concatenate con L
r r
∫ B • dl = µ 0i
L
Prof. F. Soramel
r r
∫ E • dl = 0
per campi statici
L
Fisica Generale II A.A. 2003/04
2
Le correnti concatenate vanno prese positive se
le parti concatenate dei fili sono percorse dalla
corrente concordemente al verso indicato dal
pollice della mano destra quando le altre dita
puntano nello stesso verso in cui è orientata la
linea L
Ricordando che
r r
i = ∫ j • u n dS
otteniamo
S
r r
r r
∫ B • dl = µ0 ∫ j • undS
L
S
S è una qualunque superficie
delimitata dalla linea L
Dato che la circuitazione di B è diversa da zero, B risulta essere non
conservativo e non possiamo definire un’energia potenziale magnetica
Prof. F. Soramel
Fisica Generale II A.A. 2003/04
3
Prendiamo ora un cilindro di lunghezza infinita percorso da corrente
i
Le linee di forza di B sono cerchi concentrici
con il cilindro e ad esso ⊥, l’intensità di B
dipende solo da r
a
L
r’ L’
Q
r
B’
PB
r r
∫ B • dl = B ∫ dl = BL = 2πrB
L
L
Se r > a tutta la corrente è racchiusa dalla
linea L
r r
µ 0i
B
•
d
l
=
µ
i
=
2
π
rB
⇒
B
=
0
∫L
2πr
Otteniamo così che il cilindro si comporta come un filo infinito,
ovvero come se la corrente fosse tutta concentrata sull’asse del cilindro.
La situazione cambia quando ci spostiamo all’interno del cilindro,
dobbiamo distinguere due casi
Prof. F. Soramel
Fisica Generale II A.A. 2003/04
4
1. r < a e la corrente è superficiale
r r
∫ B • dl = 0 = 2πrB ⇒ B = 0
L
B all’interno di un cilindro che porta solo corrente superficiale è nullo
2. r < a e la corrente è distribuita uniformemente su tutto il volume del
cilindro
i
r '2
2
i' = 2 πr ' = i 2
πa
a
r '2
µ0 i r '
2πr ' B = µ 0i ' = µ 0i 2 ⇒ B =
a
2π a'
B in un cilindro con corrente volumetrica è ∝ r
Prof. F. Soramel
Fisica Generale II A.A. 2003/04
5
Campo magnetico di un avvolgimento toroidale
Toroide con N spire equidistanti tutte
percorse dalla stessa corrente i.
Per simmetria abbiamo che le linee di
forza di B sono cerchi concentrici al toro
Consideriamo la linea chiusa di raggio r
che concatena tutte le spire
r r
µ 0 Ni
µ0 Ni = ∫ B • dl = BL ⇒ B =
L
L
Se il toro ha sezione trasversa di raggio
piccolo rispetto al raggio del toro, ogni
linea chiusa interna al toro ha lo stesso
raggio e B è uniforme all’interno del toro
con n = N/L spire per unità di lunghezza
B = µ 0 ni
Un percorso esterno al toro non concatena correnti quindi B = 0
Prof. F. Soramel
Fisica Generale II A.A. 2003/04
6
Campo magnetico sull’asse di un solenoide infinito con n spire/unità
di lunghezza e poco spaziate tra di loro ⇒ B uniforme e confinato nel
solenoide. Integro lungo il percorso abcd.
I lati verticali bc e da non contribuiscono
alla circuitazione in quanto B e dl sono ⊥
tra di loro.
Il lato cd non contribuisce dato che non
concatena correnti. Resta solo il lato ab
r r
r r
B • dl = ∫ B • dl = Bh
∫
abcd
ab
B = µ0 ni
r r
B
•
d
l
=
µ
nhi
0
∫
Risultato già ricavato a partire dalla legge di Ampére-Laplace
Prof. F. Soramel
Fisica Generale II A.A. 2003/04
7
In forma differenziale abbiamo
r
r
rotB = µ 0 j
r
rotE = 0
Il flusso di B vale
r r
Φ B = ∫ B • u n dS
[Φ B ] = Wb = m2 kgs −1C −1
S
Abbiamo visto che linee di forza di B sono chiuse dato che non esiste
il monopolo magnetico, di conseguenza il flusso di B attraverso una
superficie chiusa è sempre nullo
r r
Φ B = ∫ B • un dS = 0
r
divB = 0
S
Prof. F. Soramel
Fisica Generale II A.A. 2003/04
8
Equazioni di Maxwell per i campi elettrici
e magnetici statici
Forma integrale
Forma differenziale
r r
q
∫ E • undS = ε 0
r r
∫ B • u nrdS = 0
r
∫ E • dlr = 0
r
∫ B • dl = µ0i
r ρ
div E =
ε0
r
div B = 0
r
rot E = 0
r
r
rot B = µ 0 j
Prof. F. Soramel
Fisica Generale II A.A. 2003/04
9
La legge di Ampére in forma differenziale
Sul piano (xy) consideriamo un percorso rettangolare PQRS di area
molto piccola pari a dxdy.
y
S
r r
Λ B = ∫ B • dl =
R
PQRS
r r
r r
r r
r r
∫ B • dl + ∫ B • dl + ∫ B • dl + ∫ B • dl
PQ
QR
RS
SP
B
B’
dy
Lungo QR (orientato ¦ ad y) dl = dy u y
jz j
r r
r r
r r
r r
Q
uy P dx
∫QRB • dl = QR∫ B • u y dy = By dy SP∫ B • dl = − SP∫ B'•u y dy = − B' y dy
x
r r
r r
uz ux
B • dl + B • dl = (B − B ' )dy (B − B ' ) = dB
∫
QR
z
∫
y
y
y
y
y
SP
∂B y
r r
r r ∂B y
⇒ By − B' y =
dx ⇒ ∫ B • dl + ∫ B • dl =
dxdy
∂x
∂x
QR
SP
Analogamente
r r
r r
∂B x
B
•
d
l
+
B
•
d
l
=
−
dxdy
∫PQ
∫RS
∂y
Prof. F. Soramel
Fisica Generale II A.A. 2003/04
10
r r ∂By ∂Bx
dxdy
Λ B = ∫ B • dl =
−
∂
x
∂
y
PQRS
Attraverso PQRS circola la corrente di legata a j dalla relazione
r r
di = j • dS = j z dS = j z dxdy
∂B y ∂Bx
= µ 0 j z
−
∂y
∂x
Facciamo lo stesso procedimento sui piani (xz) e (yz), otteniamo
∂Bz ∂B y
= µ0 j x
−
∂z
∂y
∂Bx ∂Bz
−
= µ0 j y
∂x
∂z
Infine in tutto lo spazio abbiamo
r
r
rotB = µ 0 j
Correnti = sorgenti di
campo magnetico
Relazione locale tra B e j, ho B se so come la corrente è distribuita
nello spazio
Prof. F. Soramel
Fisica Generale II A.A. 2003/04
11