Rappresentazione doppi bipoli

Elettrotecnica II
Rappresentazioni doppi bipoli
1
Rappresentazione doppi bipoli
2
© 2004 Politecnico di Torino
1
1
Elettrotecnica II
Rappresentazioni doppi bipoli
Introduzione
3
Cosa c’è nell’Unità 5
In questa sezione si affronteranno
introduzione alle rappresentazioni dei doppi bipoli
le sei rappresentazioni classiche
tabella di trasformazione
connessioni doppi bipoli
4
© 2004 Politecnico di Torino
1
2
Elettrotecnica II
Rappresentazioni doppi bipoli
Oggetto 1/2
In questa unità saranno considerate le rappresentazioni dei
doppi bipoli nel dominio delle frequenze
Rappresentare un doppio bipolo significa precisare le sue due
equazioni costitutive che legano le tensioni e le correnti delle
due porte
5
Oggetto 2/2
I doppi bipoli che si considerano sono inerti:
assenza nel loro interno di generatori indipendenti
se le rappresentazioni sono nel dominio di Laplace gli elementi
interni si assumono inizialmente scarichi
È possibile avere la presenza di generatori pilotati nell’interno
dei doppi bipoli
6
© 2004 Politecnico di Torino
1
3
Elettrotecnica II
Rappresentazioni doppi bipoli
Introduzione
7
Rappresentazione generale
Qualsiasi doppio bipolo lineare ed inerte presenta
sicuramente la rappresentazione
A11 V1 + A12 V2 = B11 I1 + B12 I2
A21 V1 + A22 V2 = B21 I1 + B22 I 2
8
© 2004 Politecnico di Torino
1
4
Elettrotecnica II
Rappresentazioni doppi bipoli
Esempio
V1 − K V2 = 0
Trasformatore ideale
0 = I1 +
1
I
K 2
⇓
A11 = 1,
A12 = − K , B11 = 0,
A21 = 0,
A22 = 0 , B11 = 1,
B12 = 0
B12 =
1
K
9
Rappresentazione doppi bipoli
10
© 2004 Politecnico di Torino
1
5
Elettrotecnica II
Rappresentazioni doppi bipoli
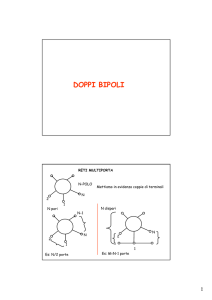
Le sei rappresentazioni classiche
11
Le sei rappresentazioni di un doppio bipolo 1/4
Le relazioni costitutive di un doppio bipolo sono due
Esse coinvolgono quattro grandezze elettriche V1, V2, I1, e I 2
Nelle relazioni costitutive due grandezze possono essere viste
come variabili indipendenti (ingressi) e le altre due come
variabili dipendenti (uscite)
12
© 2004 Politecnico di Torino
1
6
Elettrotecnica II
Rappresentazioni doppi bipoli
Le sei rappresentazioni di un doppio bipolo 2/4
I modi diversi con cui possiamo assumere due delle quattro
grandezze V1, V2, I1, e I 2 come ingressi sono in tutto sei
Esistono sei rappresentazioni che consentono di scrivere le
due equazioni di un doppio bipolo come equazioni di due
uscite in funzione di due ingressi
13
Le sei rappresentazioni di un doppio bipolo 3/4
Le sei possibilità di scegliere uscite ed ingressi differenti,
danno luogo alle sei rappresentazioni di un doppio bipolo
Non è assicurato che ogni doppio bipolo ammetta tutte e sei
le rappresentazioni. Sicuramente però ne ammette almeno
una
14
© 2004 Politecnico di Torino
1
7
Elettrotecnica II
Rappresentazioni doppi bipoli
Le sei rappresentazioni di un doppio bipolo 4/4
Le sei rappresentazioni sono classificate in tre gruppi di due
elementi ciascuno:
gruppo delle impedenze ed ammettenze
gruppo ibrido
gruppo misto
15
Le sei rappresentazioni classiche
16
© 2004 Politecnico di Torino
1
8
Elettrotecnica II
Rappresentazioni doppi bipoli
Generalità
Gruppo impedenze ed ammettenze
in questo gruppo le grandezze di ingresso e di uscita sono dello
stesso tipo:
impedenze: gli ingressi sono le correnti I1 e I2 , le uscite le
tensioni V 1 e V 2
ammettenze: gli ingressi sono le tensioni V 1 e V 2, le uscite le
correnti I1 e I2
17
Le sei rappresentazioni classiche
18
© 2004 Politecnico di Torino
1
9
Elettrotecnica II
Rappresentazioni doppi bipoli
Rappresentazione con impedenze 1/2
V1
Vettore tensione
V2
Vettore corrente
Matrice impedenze : Z =
Z11
Z12
Z 21
Z22
I1
I2
uscita
ingresso
19
Rappresentazione con impedenze 2/2
Quando essa è possibile, la rappresentazione con
impedenze (a vuoto) è definita da:
V1 = Z11 I1 + Z12 I 2
V2 = Z 21 I1 + Z 22 I 2
oppure in
forma
matriciale
V =ZI
20
© 2004 Politecnico di Torino
1
10
Elettrotecnica II
Rappresentazioni doppi bipoli
Esempio
Trasformatore ideale
A11 = 1,
A12 = − K , B11 = 0, B12 = 0
A21 = 0,
A22 = 0 , B11 = 1, B12 =
1
K
è impossibile rappresentare un trasformatore ideale con
impedenze
21
Determinazione delle impedenze 1/2
Z11
Z21
colonna
Z11 è l’impedenza vista dalla
porta 1 quando la porta 2 è
aperta
V1 = Z11 I1 + Z12 I 2
V2 = Z 21 I1 + Z 22 I 2
© 2004 Politecnico di Torino
Z11 =
V1
I1
Z 21 =
I2 = 0
V2
I1
I 2 =0
22
1
11
Elettrotecnica II
Rappresentazioni doppi bipoli
Determinazione delle impedenze 2/2
Z12
Z 22
colonna
Z22 è l’impedenza vista dalla
porta 2 quando la porta 1 è
aperta
V1 = Z11 I1 + Z12 I 2
V2 = Z21 I1 + Z 22 I 2
Z12 =
V1
I2
Z 22 =
V2
I2
I1 = 0
I1 = 0
23
Esempio con generatore pilotato 1/6
V1 = Z11 I1 + Z12 I2
V2 = Z 21 I1 + Z 22 I 2
24
© 2004 Politecnico di Torino
1
12
Elettrotecnica II
Rappresentazioni doppi bipoli
Esempio con generatore pilotato 2/6
colonna
Z11
Z21
Dalla maglia a sinistra:
V1 = s × 1 I 1 +
1
1

I1 =  s +  I1 ⇒
s ×1
s

Z11 =
V1
I1
=s+
I 2 =0
1
s
25
Esempio con generatore pilotato 3/6
colonna
Z11
Z 21
Dalla maglia a destra:
V2 =
1
1
1

I 1 + 3 V1 = I1 + 3  s +  I1
s ×1
s
s

⇒ Z 21 =
V2
I1
= 3s +
I 2 =0
4
s
26
© 2004 Politecnico di Torino
1
13
Elettrotecnica II
Rappresentazioni doppi bipoli
Esempio con generatore pilotato 4/6
colonna
Z12
Z22
Sul condensatore:
V1 =
1
1
I2 = I2 ⇒
s ×1
s
Z 12 =
V1
I2
=
I1 = 0
1
s
27
Esempio con generatore pilotato 5/6
colonna
Z12
Z22
Dalla maglia a destra:
1
1
V2 = V1 + 3 V1 = I2 + 3 I2 ⇒
s
s
Z22 =
V2
I2
=
I1 = 0
4
s
28
© 2004 Politecnico di Torino
1
14
Elettrotecnica II
Rappresentazioni doppi bipoli
Esempio con generatore pilotato 6/6
V1 = Z11 I1 + Z12 I 2
V2 = Z 21 I1 + Z 22 I 2
1
s
Z=
4
3s +
s
s+
1
s
4
s
29
Le sei rappresentazioni classiche
30
© 2004 Politecnico di Torino
1
15
Elettrotecnica II
Rappresentazioni doppi bipoli
Reciprocità
Si lavori nel dominio delle frequenze e si consideri lo stesso
multipolo inserito in due reti diverse
nel primo inserimento siano Va ed Ia i vettori di tensione e
corrente presenti sul multipolo
nel secondo inserimento siano Vb ed Ib i vettori di tensione e
corrente presenti sul multipolo
Il multipolo si dice reciproco se per qualsiasi coppia di reti in
cui il multipolo è inserito risulta:
Vat ⋅ Ib = Vbt ⋅ I a
31
Esempi di multipoli reciproci
Bipolo di impedenza
Trasformatori
Doppi bipoli inerti caratterizzati da matrici di impedenza
simmetriche
32
© 2004 Politecnico di Torino
1
16
Elettrotecnica II
Rappresentazioni doppi bipoli
Esempi di multipoli non reciproci
Amplificatori operazionali
Doppi bipoli inerti caratterizzati da matrici di impedenza non
simmetriche
33
Reti reciproche
Un rete si dice reciproca quando, resa inerte, contiene solo
elementi costituiti da elementi reciproci
La presenza di generatori pilotati e/o amplificatori
operazionali in una rete implica in generale che la rete non è
reciproca
34
© 2004 Politecnico di Torino
1
17
Elettrotecnica II
Rappresentazioni doppi bipoli
Teoremi di reciprocità
Un multipolo costituito con una rete reciproca è un multipolo
reciproco
Un multipolo reciproco non è necessariamente costituito da
una rete reciproca
35
Rappresentazione con circuito a T/1
Un doppio bipolo reciproco e rappresentabile con
impedenze, ammette una rappresentazione circuitale con
un circuito a T
Z1 = Z11 − Z12
Z2 = Z23 − Z12
Z3 = Z12
36
© 2004 Politecnico di Torino
1
18
Elettrotecnica II
Rappresentazioni doppi bipoli
Rappresentazione con circuito a T/2
Un doppio bipolo non reciproco e rappresentabile con
impedenze, ammette una rappresentazione circuitale con
un circuito a T che presenta un generatore pilotato di
tensione, su uno dei lati, per tenere conto della non
reciprocità
Z1 = Z11 − Z12
Z 2 = Z22 − Z12
Z 3 = Z 12
Eˆ = ( Z21 − Z12 ) I1
37
Esempio con trasformatore 1/3
Determinare la matrice di impedenza di un trasformatore
Rappresentare il trasformatore con un circuito a T
38
© 2004 Politecnico di Torino
1
19
Elettrotecnica II
Rappresentazioni doppi bipoli
Esempio con trasformatore 2/3
Nel dominio delle frequenze risulta:
V1 = sL1 I1 + s M I 2
V2 = sM I1 + s L2 I 2
⇒
Z=
s L1
sM
sM
s L2
39
Esempio con trasformatore 3/3
Rappresentazione con circuito a T:
V1 = sL1 I1 + s M I 2
V2 = sM I1 + s L2 I 2
⇒
40
© 2004 Politecnico di Torino
1
20
Elettrotecnica II
Rappresentazioni doppi bipoli
Le sei rappresentazioni classiche
41
Rappresentazione con ammettenze 1/2
Vettore tensione
Vettore corrente
V1
I1
I2
Matrice ammettenze : Y =
© 2004 Politecnico di Torino
ingresso
V2
uscita
Y11
Y21
Y12
Y22
42
1
21
Elettrotecnica II
Rappresentazioni doppi bipoli
Rappresentazione con ammettenze 2/2
Quando essa è possibile, la rappresentazione con
ammettenze (in corto circuito) è definita da:
I1 = Y11 V1 + Y12 V2
I 2 = Y21 V1 + Y22 V2
oppure in
forma
matriciale
I =YV
43
Esempio
Trasformatore ideale
A11 = 1,
A12 = − K , B11 = 0, B12 = 0
A21 = 0,
A22 = 0 , B11 = 1, B12 =
1
K
è impossibile rappresentare un trasformatore ideale con
ammettenze
44
© 2004 Politecnico di Torino
1
22
Elettrotecnica II
Rappresentazioni doppi bipoli
Determinazione delle ammettenze 1/2
Y11
Y21
colonna
Y11 è l’ammettenza vista dalla
porta 1 quando la porta 2 è
corto circuitata
I1 = Y11 V1 + Y12 V2
I 2 = Y21 V1 + Y22 V2
Y11 =
I1
V1 V =0
2
Y21 =
I2
V1 V =0
2
45
Determinazione delle ammettenze 2/2
colonna
Y22 è l’ammettenza vista dalla
porta 2 quando la porta 1 è
corto circuitata
I1 = Y11 V1 + Y12 V2
I 2 = Y21 V1 + Y22 V2
Y12 =
Y12
Y22
I1
V2
Y22 =
I2
V2
V1 = 0
V1 =0
46
© 2004 Politecnico di Torino
1
23
Elettrotecnica II
Rappresentazioni doppi bipoli
Legame ammettenze - impedenze
Quando un doppio bipolo è rappresentabile con impedenze
ed ammettenze risulta
Y = (Z ) −1
Z = (Y ) −1
Un doppio bipolo rappresentabile con impedenze e con
determinante nullo di Z, non ha rappresentazione con
ammettenze
Un doppio bipolo rappresentabile con ammettenze e con
determinante nullo di Y, non ha rappresentazione con
impedenze
47
Reciprocità
I doppi bipoli reciproci rappresentabili con ammettenze
hanno una matrice di ammettenze simmetrica
Y12 = Y21
48
© 2004 Politecnico di Torino
1
24
Elettrotecnica II
Rappresentazioni doppi bipoli
Esempio con trasformatore 1/6
I1 = Y11 V1 + Y12 V2
I 2 = Y21 V1 + Y22 V2
49
Esempio con trasformatore 2/6
colonna
Y11
Y21
Riportando il carico del secondario al primario
V1 = 22 ( s ×1 + 1) I1 = 4(1+ s) I1 ⇒ Y11 =
I1
V1 V
=
2 =0
1
4(s + 1)
50
© 2004 Politecnico di Torino
1
25
Elettrotecnica II
Rappresentazioni doppi bipoli
Esempio con trasformatore 3/6
colonna
Y11
Y21
Dalla maglia a destra
V1 V1
I
= = − (s × 1 + 1)I 2 = − (s + 1) I 2 ⇒ Y21 = 2
k
2
V1
=−
V2 =0
1
2(1 + s )
51
Esempio con trasformatore 4/6
colonna
Y12
Y22
Riportando il carico del secondario (corto circuito nella porta 1)
al secondario
1
s +1
V2 = ( s × 1 + 1)|| I 2 = 2
I2
s
s + s +1
⇒ Y22 =
I2
V2
=
V1 =0
s2 + s +1
s +1
52
© 2004 Politecnico di Torino
1
26
Elettrotecnica II
Rappresentazioni doppi bipoli
Esempio con trasformatore 5/6
colonna
Y12
Y22
Dalla maglia a destra
V2 = − ( s × 1 + 1)( kI 1 ) = − 2( s + 1) I 1 ⇒ Y12 =
I1
V2
=−
V1 = 0
1
= Y21
2(1 + s)
53
Esempio con trasformatore 6/6
I1 = Y11 V1 + Y12 V2
I 2 = Y21 V1 + Y22 V2
© 2004 Politecnico di Torino
Y=
1
4(1 + s)
−
1
2(1 + s )
−
1
2(1 + s)
s2 + s + 1
1+ s
54
1
27
Elettrotecnica II
Rappresentazioni doppi bipoli
Rappresentazione con circuito a Pi greca 1/2
Un doppio bipolo reciproco e rappresentabile con
ammettenze, ammette una rappresentazione circuitale
con un circuito a Pi greca. Indicando con Y 11, Y 12, Y 21, e
Y 22, le ammettenze risulta:
Y1 = Y11 + Y12
Y2 = Y22 + Y12
Y3 = −Y12
55
Rappresentazione con circuito a Pi greca 2/2
Un doppio bipolo non reciproco e rappresentabile con
ammettenze, ammette una rappresentazione circuitale
con un circuito a pi greca che presenta un generatore
pilotato di corrente su uno dei lati, per tenere conto della
non reciprocità
Y1 = Y11 + Y12
Y2 = Y23 + Y12
Y3 = −Y12
Aˆ = ( Y21 − Y12 )V1
56
© 2004 Politecnico di Torino
1
28
Elettrotecnica II
Rappresentazioni doppi bipoli
Esempio
Rappresentare il doppio bipolo avente la matrice di
ammettenza Y indicata con un circuito a Pi greca
Y=
1
4(1 + s)
−
1
2(1 + s )
−
1
2(1 + s )
s2 + s + 1
1+s
⇒ Y1 = −
1
2s 2 + s + 1
1
, Y2 =
, Y3 =
2(1 + s )
2(1 + s )
2(1 + s )
57
Le sei rappresentazioni classiche
58
© 2004 Politecnico di Torino
1
29
Elettrotecnica II
Rappresentazioni doppi bipoli
Generalità 1/2
Gruppi ibridi:
In questi due gruppi le grandezze di ingresso e di uscita non
sono dello stesso tipo:
gruppo ibrido diretto:
gli ingressi sono la corrente I1 e la tensione V 2.
Le uscite la tensione V 1 e la corrente I2.
i parametri della rappresentazione vengono chiamati parametri h
59
Generalità 2/2
gruppo ibrido inverso:
gli ingressi sono la tensione V 1 e la corrente I2, le uscite la
corrente I1 e la tensione V 2
i parametri della rappresentazione vengono chiamati parametri g
60
© 2004 Politecnico di Torino
1
30
Elettrotecnica II
Rappresentazioni doppi bipoli
Le sei rappresentazioni classiche
61
Parametri h 1/2
Vettore ingresso
Vettore uscita
Matrice ibrida : h =
h11
h 21
V1
I2
I1
V2
ingresso
uscita
h12
h22
62
© 2004 Politecnico di Torino
1
31
Elettrotecnica II
Rappresentazioni doppi bipoli
Parametri h 2/2
Per modellare transistori è molto utile la rappresentazione
con parametri h
V1 = h11 I1 + h12 V2
oppure in
forma
matriciale
I 2 = h21 I1 + h22 V2
V1
I2
=h
I1
V2
63
Esempio
Trasformatore ideale
A11 = 1, A12 = − K , B11 = 0, B12 = 0
A21 = 0, A22 = 0 , B11 = 1, B12 =
1
K
è possibile rappresentare un trasformatore ideale con
parametri h:
h=
0
K
−K
0
64
© 2004 Politecnico di Torino
1
32
Elettrotecnica II
Rappresentazioni doppi bipoli
Determinazione dei parametri h 1/2
colonna
h11 è l’impedenza vista
dalla porta 1 quando la
porta 2 è corto circuitata
V1 = h1 1 I1 + h12 V2
h11 =
h11
h 21
V1
I1 V =0
2
h21 =
I2 = h21 I1 + h22 V2
I2
I1 V = 0
2
65
Determinazione dei parametri h 2/2
colonna
h22 è l’ammettenza vista
dalla porta 2 quando la
porta 1 è aperta
V1 = h11 I1 + h12 V2
I 2 = h21 I1 + h22 V2
© 2004 Politecnico di Torino
h12 =
V1
V2
h22 =
I2
V2
h12
h 22
I1 =0
I1 =0
66
1
33
Elettrotecnica II
Rappresentazioni doppi bipoli
Reciprocità
I doppi bipoli reciproci rappresentabili con gruppo h hanno la
seguente proprietà
h12 = −h21
essendo reciproco, il trasformatore ideale rispetta questa
proprietà
67
Esempio 1/6
V1 = h11 I1 + h12 V2
I 2 = h21 I1 + h22 V2
68
© 2004 Politecnico di Torino
1
34
Elettrotecnica II
Rappresentazioni doppi bipoli
Esempio 2/6
colonna
h11
h 21
h11 è l’impedenza vista dalla porta 1 con porta 2 corto
circuitata
h11 =
V1
I1
= 10 + 5 | | 5 = 12.5Ω
V2 = 0
69
Esempio 3/6
colonna
h11
h 21
Dal partitore di corrente
I2 = −
5
1
I
I1 = − I1 ⇒ h21 = 2
5 +5
2
I1
=−
V2 = 0
1
= −0.5
2
70
© 2004 Politecnico di Torino
1
35
Elettrotecnica II
Rappresentazioni doppi bipoli
Esempio 4/6
colonna
h 12
h 22
h22 è l’ammettenza vista dalla porta 2 con porta 1 aperta
Y22 =
I2
V2
=
I1 = 0
1
1
= = 0.1 S
5 + 5 10
71
Esempio 5/6
colonna
h12
h 22
Dal partitore di tensione
V1 =
5
1
V2 = V2
5+ 5
2
⇒ h12 =
V1
V2
= 0.5 = −h21
I1 = 0
72
© 2004 Politecnico di Torino
1
36
Elettrotecnica II
Rappresentazioni doppi bipoli
Esempio 6/6
V1 = h11 I1 + h12 V2
I 2 = h21 I1 + h22 V2
h=
12.5 0.5
−0.5 0.1
73
Rappresentazione con generatori pilotati
Un doppio bipolo definito dai parametri h è rappresentabile
con il doppio bipolo in figura
74
© 2004 Politecnico di Torino
1
37
Elettrotecnica II
Rappresentazioni doppi bipoli
Le sei rappresentazioni classiche
75
Parametri ibridi g 1/2
Vettore ingresso
Vettore uscita
Matrice ibrida inversa : g =
g11
V1
I2
I1
V2
ingresso
uscita
g12
g21 g 22
76
© 2004 Politecnico di Torino
1
38
Elettrotecnica II
Rappresentazioni doppi bipoli
Parametri ibridi g 2/2
La rappresentazione ibrida inversa è definita dai parametri g
I1 = g11 V1 + g12 I 2
V2 = g 21 V1 + g 22 I 2
oppure in
forma
matriciale
I1
V2
=g
V1
I2
77
Legame h-g
Quando un doppio bipolo è rappresentabile con parametri
ibridi h e g risulta:
g = (h )− 1
h = ( g )− 1
Un doppio bipolo rappresentabile con parametri ibridi h ed
avente determinante di h nullo, non è rappresentabile con
parametri g
Un doppio bipolo rappresentabile con parametri ibridi g ed
avente determinante di g nullo, non è rappresentabile con
parametri h
78
© 2004 Politecnico di Torino
1
39
Elettrotecnica II
Rappresentazioni doppi bipoli
Determinazione dei parametri g 1/2
g11
colonna
g11 è l’ammettenza vista
dalla porta 1 quando la
porta 2 è aperta
I1 = g11 V1 + g12 I 2
V2 = g 21 V1 + g 22 I 2
g11 =
I1
V1
g 21 =
g21
I 2 =0
V2
V1
I 2 =0
79
Determinazione dei parametri g 2/2
colonna
g22 è l’impedenza vista
dalla porta 2 quando la
porta 1 è corto circuitata
g12 =
g12
g22
I1
I 2 V =0
1
I1 = g11 V1 + g12 I 2
V2 = g 21 V1 + g 22 I 2
g 22 =
V2
I2
V1 = 0
80
© 2004 Politecnico di Torino
1
40
Elettrotecnica II
Rappresentazioni doppi bipoli
Reciprocità
I doppi bipoli reciproci rappresentabili con gruppo g hanno la
seguente proprietà
g12 = − g 21
essendo reciproco, il trasformatore ideale rispetta questa
proprietà
81
Esempio con generatore pilotato 1/6
I1 = g11 V1 + g12 I 2
V2 = g 21 V1 + g 22 I 2
82
© 2004 Politecnico di Torino
1
41
Elettrotecnica II
Rappresentazioni doppi bipoli
Esempio con generatore pilotato 2/6
g11
colonna
g21
La corrente che percorre 1 ohm vale I1+2I 1=3I 1
V2 = 1× 3 I1 = 3I1
V1 = s ×1I 1 + V2 = (s + 3) I 1 ⇒ g11 =
I1
V1
=
I 2 =0
1
s +3
83
Esempio con generatore pilotato 3/6
colonna
g11
g21
Dalla maglia a sinistra
V1 = sI1 + 3I1 = ( s + 3) I1
V2 = 3 I1
⇒ g 21 =
V2
V1
=
I2 =0
3
s+3
84
© 2004 Politecnico di Torino
1
42
Elettrotecnica II
Rappresentazioni doppi bipoli
Esempio con generatore pilotato 4/6
colonna
g12
g22
La corrente che percorre 1 ohm vale: I1+2I 1+I2
La corrente che percorre 1 H vale: I1
⇒
V2 = 1× (I1 + 2 I1 + I2 ) , V2 = −s ×1 I1
I1 = −
1
I2
s+3
g12 =
I1
I2
=−
V1 =0
1
s+3
85
Esempio con generatore pilotato 5/6
colonna
g12
g22
V2 = 1 × (I1 + 2 I1 + I2 ) = − s × 1I1
⇓
I1 = −
1
I2
s +3
⇓
s
V2 =
I2
s +3
⇒
g 22 =
V2
I2
=
V1 = 0
s
s+3
86
© 2004 Politecnico di Torino
1
43
Elettrotecnica II
Rappresentazioni doppi bipoli
Esempio con generatore pilotato 6/6
I1 = g11 V1 + g12 I 2
V2 = g 21 V1 + g 22 I 2
1
s+3
g=
3
s+3
1
s+3
s
s +3
−
87
Le sei rappresentazioni classiche
88
© 2004 Politecnico di Torino
1
44
Elettrotecnica II
Rappresentazioni doppi bipoli
Generalità 1/2
Gruppi misti
in questi due gruppi le grandezze di ingresso e di uscita
sono definite in porte separate
gruppo misto diretto:
gli ingressi sono la tensione V 2 e la corrente -I2 della
porta 2.
Le uscite la tensione V 1 e la corrente I1 della porta 1
89
Generalità 2/2
i parametri della rappresentazione vengono chiamati parametri
A,B,C,D
gruppo misto inverso:
gli ingressi sono la tensione V 1 e la corrente -I1 della porta 1.
Le uscite la tensione V 2 e la corrente I2 della porta 2
i parametri della rappresentazione vengono chiamati parametri
A’,B’,C’,D’
90
© 2004 Politecnico di Torino
1
45
Elettrotecnica II
Rappresentazioni doppi bipoli
Le sei rappresentazioni classiche
91
Parametri A,B,C,D 1/2
V2
Vettore ingresso
Vettore uscita
Matrice di trasmissione : T =
-I2
V1
I1
A B
C D
92
© 2004 Politecnico di Torino
1
46
Elettrotecnica II
Rappresentazioni doppi bipoli
Parametri A,B,C,D 2/2
Per modellare doppi bipoli è molto utile la rappresentazione
con parametri A, B, C, D
oppure in
forma
matriciale
V1 = AV2 + B (−I 2 )
I1 = C V2 + D (− I 2 )
V1
V
=T 2
I1
− I2
93
Esempio
Trasformatore ideale
A11 = 1,
A1 2 = − K ,
B11 = 0,
B12 = 0
A21 = 0,
A22 = 0 , B11 = 1, B12 =
1
K
è possibile rappresentare un trasformatore ideale con
parametri A, B, C, D
A
T=
C
© 2004 Politecnico di Torino
K
B
=
D 0
0
1
K
94
1
47
Elettrotecnica II
Rappresentazioni doppi bipoli
Determinazione dei parametri A, B, C, D 1/2
colonna
A
C
conviene alimentare dalla porta 1
V1 = A V2 + B( − I 2 )
I1 = C V2 + D (− I 2 )
A=
V1
V2
C=
I1
V2
I 2 =0
I2 = 0
95
Determinazione dei parametri A, B, C, D 2/2
colonna
B
D
conviene alimentare dalla porta 1
V1 = AV2 + B(− I 2 )
I1 = C V2 + D ( − I 2 )
© 2004 Politecnico di Torino
B=−
V1
I2
D=−
V2 =0
I1
I2
V2 =0
96
1
48
Elettrotecnica II
Rappresentazioni doppi bipoli
Reciprocità
I doppi bipoli reciproci rappresentabili con gruppo misto
hanno la seguente proprietà
det[T ] = AD − BC = 1
essendo reciproco, il trasformatore ideale rispetta questa
proprietà
97
Esempio con generatore pilotato 1/6
V1 = AV2 + B ( − I 2 )
I1 = C V2 + D ( − I 2 )
98
© 2004 Politecnico di Torino
1
49
Elettrotecnica II
Rappresentazioni doppi bipoli
Esempio con generatore pilotato 2/6
colonna
A
C
Considerando il nodo B
V1 − V2
V
+ 2V1 = 2
2
3
⇒ V1 =
V2
3
⇒A=
V1
V2
=
I2 =0
1
3
99
Esempio con generatore pilotato 3/6
colonna
A
C
Dal nodo A
I1 =
I
V1 V1 − V2 1 V2 (1/3)V2 − V2
+
=
+
=0 ⇒ C= 1
V2
1
2
3 1
2
=0
I2 =0
100
© 2004 Politecnico di Torino
1
50
Elettrotecnica II
Rappresentazioni doppi bipoli
Esempio con generatore pilotato 4/6
B
D
colonna
V2=0 implica che la corrente sul resistore 3 è nulla.
Dal nodo B
V1 − V2
V
V
+ 2V1 + I 2 = 1 + 2V1 + I2 = 0 ⇒ I 2 = − 5 1
2
2
2
⇒ B =−
V1
2
=
I 2 V =0 5
2
101
Esempio con generatore pilotato 5/6
colonna
B
D
⇒ D=−
I1
I2
Dal nodo A
I1 =
V1 V1 − V 2 V 1 V1 3
3
2
3
+
= + = V1 = × ( − I 2 ) = − I 2
1
2
1 2 2
2
5
5
=
V2 = 0
3
5
102
© 2004 Politecnico di Torino
1
51
Elettrotecnica II
Rappresentazioni doppi bipoli
Esempio con generatore pilotato 6/6
V1 = AV2 + B( − I 2 )
I1 = C V2 + D ( − I 2 )
1
T= 3
0
2
5
3
5
103
Le sei rappresentazioni classiche
104
© 2004 Politecnico di Torino
1
52
Elettrotecnica II
Rappresentazioni doppi bipoli
Parametri A’, B’, C’, D’ 1/2
Vettore ingresso
Vettore uscita
Matrice di trasmissione inversa T ' =
V1
-I1
V2
I2
A' B '
C' D'
105
Parametri A’, B’, C’, D’ 2/2
Nel gruppo misto inverso (parametri A’, B’, C’, D’) il ruolo
delle porte è invertito
V2 = A ' V1 + B '(− I1 )
I 2 = C ' V1 + D '(− I1 )
oppure in
forma
matriciale
V2
I2
=T'
V1
− I1
106
© 2004 Politecnico di Torino
1
53
Elettrotecnica II
Rappresentazioni doppi bipoli
Esempio
Trasformatore ideale
A11 = 1,
A12 = − K , B11 = 0, B12 = 0
A21 = 0,
A22 = 0 , B11 = 1, B12 =
1
K
è possibile rappresentare un trasformatore ideale con
parametri A’, B’, C’, D’
1
T '=
= K
C ' D'
0
A'
B'
0
K
107
Legame T-T’
Quando un doppio bipolo è rappresentabile con parametri
misti A, B, C, D e A’, B’, C’, D’ risulta
T'=
T=
A' B '
C' D'
=
1
0
0 −1
(T )−1
1
0
0 −1
A B 1 0
1 0
=
(T ') −1
C D 0 −1
0 −1
108
© 2004 Politecnico di Torino
1
54
Elettrotecnica II
Rappresentazioni doppi bipoli
Determinazione dei parametri A’, B’, C’, D’ 1/2
A'
C'
colonna
conviene alimentare dalla porta 2
V2 = A ' V1 + B '(−I1 )
I 2 = C ' V1 + D '(− I1 )
A' =
V2
V1
C '=
I2
V1
I 1= 0
I1 =0
109
Determinazione dei parametri A’, B’, C’, D’ 2/2
colonna
B'
D'
conviene alimentare dalla porta 2
V2 = A ' V1 + B '( − I1)
I 2 = C ' V1 + D '( − I1 )
© 2004 Politecnico di Torino
B'= −
V2
I1
D'= −
V1 =0
I2
I1
V1 =0
110
1
55
Elettrotecnica II
Rappresentazioni doppi bipoli
Reciprocità
I doppi bipoli reciproci rappresentabili con gruppo misto
inverso hanno la seguente proprietà
det[T '] = A ' D '− B ' C ' = 1
essendo reciproco, il trasformatore ideale rispetta questa
proprietà
111
Esempio 1/4
V2 = A ' V1 + B '(− I 1 )
I 2 = C ' V1 + D '(− I1 )
112
© 2004 Politecnico di Torino
1
56
Elettrotecnica II
Rappresentazioni doppi bipoli
Esempio 2/4
colonna
A'
C'
Non c’è caduta di tensione sul resistore
V1 = V2 ⇒
Sul condensatore
A' =
V1 =
V2
V1
=1
I1 = 0
1
I2 ⇒
s
C' =
I2
V1
=s
I 1 =0
113
Esempio 3/4
colonna
B'
D'
La tensione sul condensatore uguaglia quella sul resistore
V2 =
I1 + I2
= − I1 ⇒ I 2 = − (s + 1) I1
s
⇒ D'= −
I2
I1
= s +1
V1 =0
La tensione sul resistore vale
V2 = −1× I1 = − I1 ⇒
© 2004 Politecnico di Torino
B' = −
V2
I1
=1
V1 =0
114
1
57
Elettrotecnica II
Rappresentazioni doppi bipoli
Esempio 4/4
V2 = A ' V1 + B '( − I1 )
I2 = C ' V1 + D '(− I1 )
⇒
T' =
1
1
s s +1
il doppio bipolo è composto di elementi reciproci quindi e
reciproco
det[T '] = 1
115
Rappresentazione doppi bipoli
116
© 2004 Politecnico di Torino
1
58
Elettrotecnica II
Rappresentazioni doppi bipoli
Tabella di trasformazione
117
Le sei rappresentazioni 1/3
Gruppo impedenze ed ammettenze
impedenze
ammettenze
V1 Z11
=
V2 Z 21
Z12 I1
I
=Z 1
Z 22 I 2
I2
I1 Y11 Y12 V1
V
=
=Y 1
I 2 Y21 Y22 V2
V2
118
© 2004 Politecnico di Torino
1
59
Elettrotecnica II
Rappresentazioni doppi bipoli
Le sei rappresentazioni 2/3
Gruppi ibridi
diretto
inverso
V1 h11
=
I 2 h 21
I1
V2
=
h12 I1
I1
=h
h22 V2
V2
g 11
g 12 V1
g 21
g 22 I 2
=g
V1
I2
119
Le sei rappresentazioni 3/3
Gruppi misti
diretto
V1 A
=
I1 C
inverso
V2
I2
=
B V2
V
=T 2
−I2
D − I2
A'
B ' V1
C'
D ' − I1
=T '
V1
−I1
120
© 2004 Politecnico di Torino
1
60
Elettrotecnica II
Rappresentazioni doppi bipoli
Tabella di trasformazione
121
Z in funzione di Y e viceversa
V1
V2
=
Z11
Z12 I 1
Z 21 Z 22 I 2
=Z
I1
I2
I 1 Y11 Y12 V1
V1
=
=Y
I 2 Y21 Y22 V2
V2
Y22
det[Y ]
Z=
Y
− 21
det[Y ]
Y12
det[Y ]
Y11
det[Y ]
−
Y=
Z 22
det[ Z ]
−
Z21
det[ Z ]
−
Z12
det[ Z ]
Z11
det[Z ]
122
© 2004 Politecnico di Torino
1
61
Elettrotecnica II
Rappresentazioni doppi bipoli
Z in funzione di h e viceversa
V1 Z11
=
V2 Z 21
Z12 I1
I1
=Z
Z 22 I 2
I2
V1
h11
h12 I1
h 21
h22 V2
I2
Z=
det[ h]
h22
−
h21
h22
h12
h22
1
h22
=
h=
det[ Z ]
Z 22
−
Z 21
Z 22
=h
I1
V2
Z12
Z 22
1
Z 22
123
Z in funzione di g e viceversa
V1
V2
=
Z11
Z12 I1
Z 21
Z22 I2
I1 g 1 1
=
V2 g 21
1
g11
Z=
g 21
g11
g12
g11
det[ g ]
g11
−
g=
=Z
I1
I2
g12 V1
V
=g 1
g 22 I 2
I2
1
Z11
−
Z12
Z11
Z 21
Z11
det[Z ]
Z11
124
© 2004 Politecnico di Torino
1
62
Elettrotecnica II
Rappresentazioni doppi bipoli
Z in funzione di T e viceversa
V1
V2
=
Z11
Z12 I1
Z 21
Z 22 I 2
V1 A
=
I1 C
A
C
Z=
1
C
det[T ]
C
D
C
T=
=Z
I1
I2
B V2
V2
=T
D − I2
−I 2
Z11
Z 21
det[ Z ]
Z 21
1
Z 21
Z 22
Z 21
125
Z in funzione di T’ e viceversa
V1
V2
=
Z11
Z12 I1
Z 21 Z 22 I 2
=Z
I1
I2
V2
A ' B ' V1
V1
=
=T '
I 2 C ' D ' − I1
−I1
D'
C'
Z=
det[T ']
C'
1
C'
A'
C'
Z 22
Z
T ' = 12
1
Z12
det[Z ]
Z12
Z12
Z12
126
© 2004 Politecnico di Torino
1
63
Elettrotecnica II
Rappresentazioni doppi bipoli
Tabella di trasformazione
127
Y in funzione di h e viceversa
I1
I2
V1
I2
Y=
1
h11
−
h12
h11
h21
h11
det[ h]
h11
=
=
Y11
Y12 V1
=Y
V1
=h
I1
Y 21 Y22 V2
h11
h12 I1
h 21 h22 V2
1
Y11
h=
Y21
Y11
V2
V2
Y12
Y11
det[Y ]
Y11
−
128
© 2004 Politecnico di Torino
1
64
Elettrotecnica II
Rappresentazioni doppi bipoli
Y in funzione di g e viceversa
I1 Y11 Y12 V1
V
=
=Y 1
I2 Y 21 Y22 V2
V2
I1
V2
Y=
det[ g ]
g 22
g12
g 22
g
− 21
g 22
1
g 22
g=
g 11
g12 V1
g 21
g 22 I2
det[Y ]
Y22
Y12
Y22
Y21
Y22
1
Y22
=
−
=g
V1
I2
129
Y in funzione di T e viceversa
I1
I2
V1
I1
D
B
Y=
1
−
B
−
det[T ]
B
A
B
−
T=
−
=
=
Y22
Y21
Y11
Y12 V1
Y21 Y22 V2
A
C
=Y
V1
V2
V
B V2
=T 2
−I2
D − I2
−
1
Y21
det[Y ]
Y
− 11
Y21
Y21
130
© 2004 Politecnico di Torino
1
65
Elettrotecnica II
Rappresentazioni doppi bipoli
Y in funzione di T’ e viceversa
I1 Y11 Y12 V1
V
=
=Y 1
I2 Y 21 Y22 V2
V2
V2
I2
A'
1
−
B'
B'
Y=
det[T '] D '
−
B'
B'
=
V
A ' B ' V1
=T ' 1
C ' D ' − I1
− I1
−
T'=
−
Y11
Y12
−
1
Y12
det[Y ]
Y
− 22
Y12
Y12
131
Tabella di trasformazione
132
© 2004 Politecnico di Torino
1
66
Elettrotecnica II
Rappresentazioni doppi bipoli
h in funzione di g e viceversa
V1
I2
I1
V2
g22
g
− 12
det[ g ]
det[ g ]
h=
g
g11
− 21
det[ g ] det[ g ]
=
=
h11
h12 I1
h 21
h22 V2
g 11
g12 V1
g 21
g22 I 2
=h
=g
I1
V2
V1
I2
h22
h
− 12
det[ h ]
det[ h ]
g=
h21
h11
−
det[ h] det[h ]
133
h in funzione di T e viceversa
V1 h11
=
I 2 h21
h12 I1
I
=h 1
h22 V2
V2
V1
V
B V2
=T 2
−I2
D − I2
I1
B
h= D
1
−
D
det[T ]
D
C
D
=
A
C
−
T=
det[h ]
h
− 11
h21
h21
−
h22
h21
−
1
h21
134
© 2004 Politecnico di Torino
1
67
Elettrotecnica II
Rappresentazioni doppi bipoli
h in funzione di T’ e viceversa
V1
I2
V2
I2
B'
A'
h=
det[T ']
−
A'
1
A'
C'
A'
=
=
h11
h12 I1
h 21
h22 V2
A ' B ' V1
C ' D ' − I1
1
h12
T '=
h22
h12
=h
I1
V2
=T '
V1
− I1
h11
h12
det[h]
h12
135
Tabella di trasformazione
136
© 2004 Politecnico di Torino
1
68
Elettrotecnica II
Rappresentazioni doppi bipoli
g in funzione di T e viceversa
I1
V2
=
g 11
g12 V1
g 21
g 22 I 2
V1 A
=
I1 C
C
A
g=
1
A
−
det[T ]
A
B
A
T=
=g
V1
I2
B V2
V2
=T
D − I2
−I 2
1
g 21
g 22
g 21
g 11
g 21
det[ g ]
g 21
137
g in funzione di T’ e viceversa
I1
V2
V2
I2
C'
1
−
D'
D'
g=
det[T '] B '
D'
D'
=
=
g12 V1
g 21
g 22 I 2
A ' B ' V1
C ' D ' − I1
−
T '=
g 11
=g
V1
=T '
I2
V1
− I1
det[ g ]
g
− 22
g12
g12
−
g 11
g12
−
1
g12
138
© 2004 Politecnico di Torino
1
69
Elettrotecnica II
Rappresentazioni doppi bipoli
Tabella di trasformazione
139
T in funzione di T’ e viceversa
V1
I1
=
V
A B V2
=T 2
C D −I 2
−I 2
V2
A ' B ' V1
V1
=
=T '
I 2 C ' D ' − I1
−I1
D'
det[T ']
T=
C'
det[T ]
B'
det[T ]
A'
det[T ]
D
det[T ]
T '=
C
det[T ]
B
det[T ]
A
det[T ]
140
© 2004 Politecnico di Torino
1
70
Elettrotecnica II
Rappresentazioni doppi bipoli
Rappresentazione doppi bipoli
141
Connessioni doppi bipoli
142
© 2004 Politecnico di Torino
1
71
Elettrotecnica II
Rappresentazioni doppi bipoli
Connessioni: Generalità
I bipoli hanno solo due possibilità di connessione:
serie
parallelo
Avendo due porte i doppi bipoli hanno una maggiore possibilità di
connessioni
tuttavia, se le porte non sono intrinseche, è importante
verificare che le eventuali connessioni mantengano la proprietà
di porta
143
Connessioni: Generalità
Le possibili connessioni di doppi bipoli
connessioni serie su entrambe le porte (serie-serie)
connessioni parallelo su entrambe le porte (parallelo-parellelo)
connessioni ibride:
serie sulle porte 1 e parallelo sulle porte 2 (serie-parallelo)
parallelo sulle porte 1 e serie sulle porte 2 (parallelo-serie)
connessioni a cascata
144
© 2004 Politecnico di Torino
1
72
Elettrotecnica II
Rappresentazioni doppi bipoli
Connessioni serie-serie
La porta 11’ del doppio bipolo A e la porta 11’ del doppio bipolo B
sono percorse dalla stessa corrente
La porta 22’ del doppio bipolo A e la porta 22’ del doppio bipolo B
sono percorse dalla stessa corrente
Se entrambi i doppi bipoli sono rappresentabili con impedenze ZA e
Zb , anche il doppio bipolo ottenuto dalla connessione serie-serie è
rappresentabile con impedenze Z e si ha:
Z= ZA + Zb
145
Connessioni parallelo-parallelo
Sulla porta 11’ del doppio bipolo A e sulla porta 11’ del doppio
bipolo B è applicata la stessa tensione
Sulla porta 22’ del doppio bipolo A e sulla porta 22’ del doppio
bipolo B è applicata la stessa tensione
Se entrambi i doppi bipoli sono rappresentabili con ammettenze YA
e Yb , anche il doppio bipolo ottenuto dalla connessione paralleloparallelo è rappresentabile con ammettenze Y e si ha:
Y= Y A + Yb
146
© 2004 Politecnico di Torino
1
73
Elettrotecnica II
Rappresentazioni doppi bipoli
Connessioni serie-parallelo
Sulla porta 11’ del doppio bipolo A e sulla porta 11’ del doppio
bipolo B è applicata la stessa corrente
Sulla porta 22’ del doppio bipolo A e sulla porta 22’ del doppio
bipolo B è applicata la stessa tensione
Se entrambi i doppi bipoli sono rappresentabili con parametri ibridi
diretti hA e hb , anche il doppio bipolo ottenuto dalla connessione
serie-parallelo è rappresentabile con parametri h e si ha:
h= hA + hb
147
Connessioni parallelo-serie
Sulla porta 11’ del doppio bipolo A e sulla porta 11’ del doppio
bipolo B è applicata la stessa tensione
La porta 22’ del doppio bipolo A e la porta 22’ del doppio bipolo B
sono percorse dalla stessa corrente
Se entrambi i doppi bipoli sono rappresentabili con parametri ibridi
inversi gA e gb , anche il doppio bipolo ottenuto dalla connessione
serie-parallelo è rappresentabile con parametri g e si ha:
g= gA + gb
148
© 2004 Politecnico di Torino
1
74
Elettrotecnica II
Rappresentazioni doppi bipoli
Connessione in cascata 1/2
La porta 22’ del doppio bipolo A e connessa alla porta 11’ del
doppio bipolo B
La porta 11’ del doppio bipolo A e la porta 22’ del doppio bipolo B
sono le due porte accessibili del doppio bipolo ottenuto dalla
cascata del doppio bipolo A con il doppio bipolo B
149
Connessione in cascata 2/2
Se entrambi i doppi bipoli sono rappresentabili con matrici di
trasmissione T A e Tb , anche il doppio bipolo ottenuto dalla
connessione a cascata è rappresentabile con matrice di
trasmissione T e si ha:
T= T A x T b
La connessione a cascata tra doppi bipoli costituisce la più
importante ed utilizzata connessione di doppi bipoli
150
© 2004 Politecnico di Torino
1
75
Elettrotecnica II
Rappresentazioni doppi bipoli
Connessioni doppi bipoli
151
Connessioni serie-serie esempio 1
Determinare i parametri Z del doppio bipolo indicato in figura
Determinare i parametri h dello stesso doppio bipolo
il doppio bipolo equivale alla connessione serie-serie dei due
doppi bipoli indicati in figura
152
© 2004 Politecnico di Torino
1
76
Elettrotecnica II
Rappresentazioni doppi bipoli
Connessioni serie-serie esempio 2
Per il doppio bipolo in alto si ha:
Z11a = 1 +
1
s
1
Z12a =
s
a
Z21
=
1
s
1
Z22a = s +
s
Za =
1+
1
s
1
s
1
s
s+
1
s
153
Connessioni serie-serie esempio 3
Per il doppio bipolo in basso si ha:
Z11b = 1 + 2 = 3
Z 21b = 1
Z12b = 1
b
Z 22
= 2 + 1= 3
Zb =
3 1
1 3
154
© 2004 Politecnico di Torino
1
77
Elettrotecnica II
Rappresentazioni doppi bipoli
Connessioni serie-serie esempio 4
1/2
Il doppio bipolo ottenuto dalla connessione serie-serie
presenta una matrice di impedenza che è la somma delle
matrici di impedenza
1
1
1+
s
s
Z = Za +Zb =
1
1
1+
3+ s+
s
s
4+
155
Connessioni serie-serie esempio 4 2/2
Il gruppo misto h si ottiene con le formule di trasformazione
det[ Z ]
Z 22
h=
Z
− 21
Z 22
© 2004 Politecnico di Torino
Z12
4s 2 + 12s + 5
2
Z 22
= s + 3s + 1
1
s +1
− 2
Z 22
s + 3s + 1
s +1
s + 3s + 1
s
2
s + 3s + 1
2
156
1
78
Elettrotecnica II
Rappresentazioni doppi bipoli
Connessioni parallelo-parallelo esempio 1
Determinare i parametri Y del doppio bipolo indicato in figura
Determinare la matrice di trasmissione dello stesso doppio bipolo
il doppio bipolo equivale alla connessione parallelo-parallelo dei
due doppi bipoli indicati a destra
157
Connessioni parallelo-parallelo esempio 2
Per il doppio bipolo in alto si ha:
Ya =
1.5 + 2.5s
−(0.5 + 0.5s)
−(0.5 + 0.5s )
2.5 + s
158
© 2004 Politecnico di Torino
1
79
Elettrotecnica II
Rappresentazioni doppi bipoli
Connessioni parallelo-parallelo esempio 3
Per il doppio bipolo in basso si ha:
Yb =
0 0
G 0
159
Connessioni parallelo-parallelo esempio 4 1/2
Il doppio bipolo ottenuto dalla connessione parallelo parallelo presenta una matrice di ammettenze che è la
somma delle matrici di ammettenze
Y = Ya +Yb =
1.5 + 2.5s
−(0.5 + 0.5s)
G − (0.5 + 0.5 s)
2.5 + s
160
© 2004 Politecnico di Torino
1
80
Elettrotecnica II
Rappresentazioni doppi bipoli
Connessioni parallelo-parallelo esempio 4
2/2
La matrice di trasmissione si ottiene utilizzando le formule di
trasformazione
−5 − 2 s
1 + 2G + s
T=
=
16 + 2 G(1 + s ) + 11s (3 + s )
det[Y ]
Y
−
− 11 −
Y21
Y21
2(1 + 2G + s )
−
Y22
Y21
−
1
Y21
2
1 + 2G + s
−3 − 5s
1 + 2G + s
−
161
Connessione in cascata esempio 1
I doppi bipoli A e B sono connessi in cascata
Il doppio bipolo B ha i seguenti parametri di impedenza
Zb =
20 5
5 10
Il doppio bipolo complessivo ha i seguenti parametri di
impedenza
Z=
25 5
5 10
Determinare i parametri di ammettenza e di impedenza del
doppio bipolo A
162
© 2004 Politecnico di Torino
1
81
Elettrotecnica II
Rappresentazioni doppi bipoli
Connessione in cascata esempio 2
Matrice di trasmissione T b del doppio bipolo B
Tb =
Z11b
Z 2b1
det[Z ]
Z 21b
1
Z 2b1
Z 22
Z 21b
b
20
5
=
1
5
20 × 10 − 5 ×5
4 35
5
= 1
10
2
5
5
Matrice di trasmissione T del doppio bipolo complessivo
T = T a ⋅T b =
Z11
Z 21
det[Z ]
Z21
1
Z 21
Z22
Z21
25
5
=
1
5
25 × 10 − 5 × 5
5
5
= 1
10
5
5
45
2
163
Connessione in cascata esempio 3
Matrice di trasmissione T a del doppio bipolo A
5
T a = T ⋅ (T b )− 1 = 1
5
45 4
1
2
5
35
2
−1
=
1 5
0 1
164
© 2004 Politecnico di Torino
1
82
Elettrotecnica II
Rappresentazioni doppi bipoli
Connessione in cascata esempio 4
Parametri Y a del doppio bipolo A
Da
a
Ya = B
1
− a
B
−
det[T a ]
1
a
5
B
=
1
Aa
−
a
5
B
1
5
1
5
−
Ta =
1 5
0 1
Parametri Za del doppio bipolo A
Aa
a
Za = C
1
Ca
© 2004 Politecnico di Torino
det[T a ]
∞ ∞
Ca
=
a
∞ ∞
D
a
C
non esistono !
165
1
83