FAM
Serie 39: Meccanica VI
C. Ferrari
Esercizio 1 Diffusione e parametro d’impatto
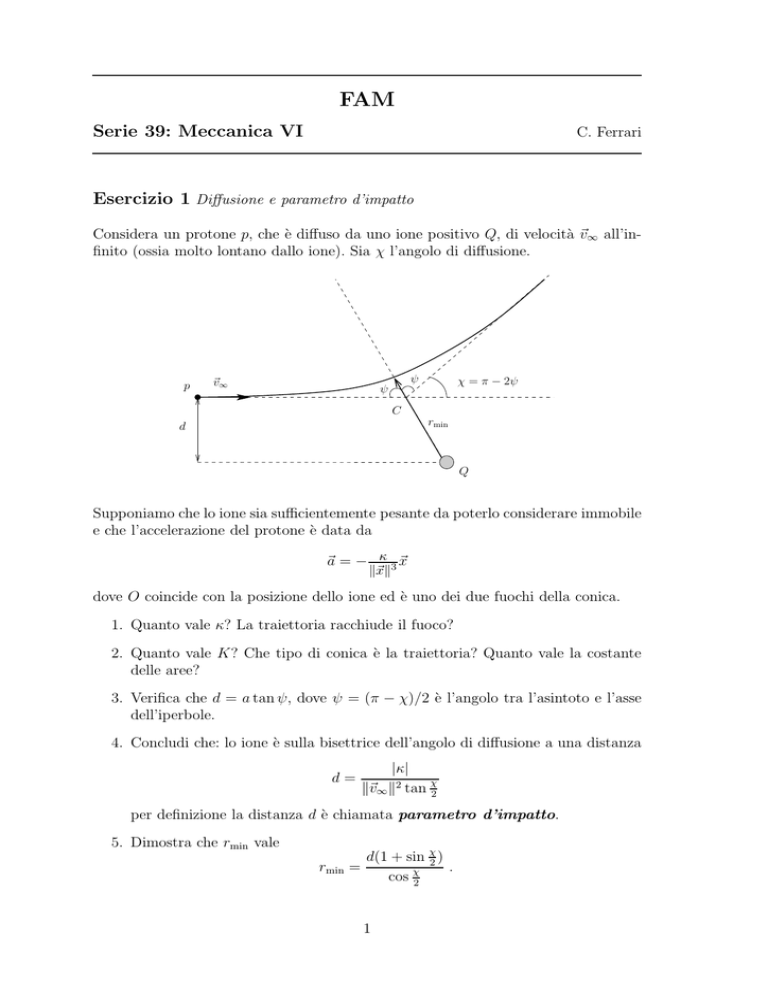
Considera un protone p, che è diffuso da uno ione positivo Q, di velocità ~v∞ all’infinito (ossia molto lontano dallo ione). Sia χ l’angolo di diffusione.
p
~v∞
ψ
ψ
χ = π − 2ψ
C
rmin
d
Q
Supponiamo che lo ione sia sufficientemente pesante da poterlo considerare immobile
e che l’accelerazione del protone è data da
~a = − κ 3 ~x
k~xk
dove O coincide con la posizione dello ione ed è uno dei due fuochi della conica.
1. Quanto vale κ? La traiettoria racchiude il fuoco?
2. Quanto vale K? Che tipo di conica è la traiettoria? Quanto vale la costante
delle aree?
3. Verifica che d = a tan ψ, dove ψ = (π − χ)/2 è l’angolo tra l’asintoto e l’asse
dell’iperbole.
4. Concludi che: lo ione è sulla bisettrice dell’angolo di diffusione a una distanza
d=
|κ|
k~v∞ k2 tan χ2
per definizione la distanza d è chiamata parametro d’impatto.
5. Dimostra che rmin vale
rmin =
d(1 + sin χ2 )
.
cos χ2
1
Esercizio 2 Diffusione ed esperienza di Rutherford
1. Un protone di velocità v∞ = 4·103 m/s è diffuso da uno ione pesante, immobile,
dei carica e = 1,6 · 10−19 C. Si osserva che l’angolo di diffusione χ è uguale a
30◦ . Qual è il valore del parametro d’impatto? e quanto vale rmin ?
2. Nell’esperienza di Rutherford sulla scoperta nel nucleo atomico si è osservata
la diffusione di particelle α ad opera di nuclei di oro (Z = 79). Nell’esperienza
si sono rilevati anche angoli molto grandi, per esempio χ = 160◦. Supponendo
che v∞ = 2 · 107 m/s quanto vale il parametro d’impatto? e quanto vale rmin ?
Considerando rmin come taglia massima del nucleo atomico qual è l’ordine di
grandezza di un nucleo? Confronta con quello di un atomo che è circa 10−10 m.
Esercizio 3 Moto centrale
Si osserva che:
• il moto di un corpo è centrale di centro O;
−→
• l’angolo α tra il vettore posizione ~x = OP e il vettore velocità è costante.
Vefifica che l’accelerazione è data da
2
C
1 ~e ,
~a = −
3 r
sin α
r
dove C è la costante delle aree.
Indicazione: Considera ~x · ~v .
Esercizio 4 Leggi di Keplero generalizzate
Considera il problema a due corpi in moto centrale e di massa m1 e m2 . Sia
m m2
~ = ~x ∧ µ~x˙ il
µ = m 1+ m
la massa ridotta, M = m1 + m2 la massa totale, L
1
2
momento angolare relativo. Dimostra che le leggi di Keplero generalizzate sono
• prima legge
r=
L2 /µ2
,
GM(1 + e cos θ)
• seconda legge
dA = 1 L ,
2µ
dt
• terza legge
2
T 2 = 4π a3 .
GM
2
Indicazione: Approfondisci la formalizzazione del problema a due corpi con forza
centrale.
Osservazione: Le leggi scoperte da Keplero sono in realtà solo approssimativamente
corrette, esse hanno permesso di ottenere la legge della gravitazione di Newton, a
partire dalla quale è possibile derivare a posteriori le leggi di Keplero generalizzate!
Il fatto che leggi “approssimative” hanno condotto alla legge fondamentale della
gravitazione è da ricondurre al fatto che la massa del Sole e molto più grande di
quella dei pianeti cosicché M ≈ mS e mP è trascurabile.
Esercizio 5 Massa del satellite Io di Giove
Il periodo orbitale del satellite Io di Giove è di 1,77 d = 1,53 · 105 s, si osserva che il
semi-asse maggiore è a = 4,22 · 108 m. Supponendo che la massa di Io è trascurabile
rispetto a quella di Giove, determina la massa di Giove.
3