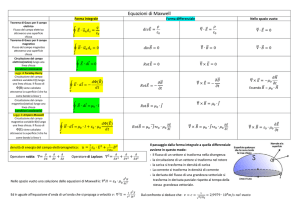
4.2. Integrazione complessa.
4.2.1. Campo vettoriale associato ad una funzione complessa. Alla funzione complessa H(z) = u(x, y) + iv(x, y) si può associare il campo vettoriale nel
piano H(r) = u(r)ex +v(r)ey , r = (x, y), oppure il campo vettoriale “coniugato”1
H = u(r)ex + v(r)ey .
Viceversa, a un dato un campo vettoriale H = Hx ex + Hy ey si può associare la
funzione complessa H(z) = H(x + iy) = Hx (x, y) + iHy (x, y) oppure la funzione
complessa H = Hx − iHy . A questo stadio iniziale potrà sembrare strano, ma
l’associazione naturale è quella “coniugata”.
N.B. Con abuso di notazione, potremmo parlare di campo f (z) associato alla
funzione f (z). In questo caso la cautela è d’obbligo: quando diciamo “campo
f (z)” indentiamo che si consideri f (z) non come una funzione complessa, ma
come una funzione vettoriale del vettore r = (x, y), che ha u = u(x, y) come
componente-x e −v = −v(x, y) come componente-y.
4.2.2. Integrazione. Sull’integrazione complessa c’è poco da dire, senza saperlo,
la conoscete già: dato un cammino regolare K nel piano complesso dal punto z1
al puntoz2 , l’integrale di linea
Z
H(z)dz
K
significa
Z
udx − vdy + i
(u + iv)(dx + idy) =
H(z)dz =
udy + vdx
K
K
K
K
Z
Z
Z
Quindi la nozione di integrale di una funzione complessa è ricondotta a quella di
integrale di linea nel piano, che si assume noto dall’analisi reale. Le nozioni di
continuità della curva e di regolarità (esistenza della tangente) sono le stesse sia
che si riguardi il piano come C sia come R2 .
Si vede facilmente che la parte reale e la parte immaginaria dell’integrale hanno
una naturale interpretazione geometrica in termini del campo vettoriale coniugato,
si ha infatti
Z
Z
Z
udx − vdy = =
udx + (−v)dy =
H • T ds
K
K
K
Z
Z
Z
udy + vdx = =
udy − (−v)dx
H • N ds
K
K
K
invalso l’uso di chiamare campo di Polya il campo f¯ associato alla funzione complessa f ,
perchè questa associazione è discussa e utilizzata nel libro di analisi complessa di Polya. Polya è
stato un grande matematico, ma questa (tutto sommato) piccola cosa è un trucco noto ai fisici
da molto tempo. Per questo si è preferito il termine neutro “coniugato”.
1È
1
2
p
dove ds = |dr| = (dx)2 + (dy 2 ) è la lunghezza infinitesima di un arco di curva,
e N sono rispettivamente il versore tangente e il versore normale alla curva, cioè
T ds = dr = (dx, dy) e N ds = (dy, −dx).
In coordinate polari il significato geometrico di Hdz è ancora più trasparente.
Siano β e α gli angoli di H e dz rispettivamente, allora
Hdz = Heiβ eiα ds .
Detto θ è l’angolo tra H e dz, si vede facilmente dalla figura
che
Heiβ eiα ds = |H|eiθ ds ,
e quindi che
H| cos θ + iH| sin θ ds
= H • T + H • N ds
Hdz =
= H • dr + H • N ds
4.2.3. Circuitazione e Flusso. Consideriamo adesso il caso in cui il cammino
d’integrazione sia un circuito, descritto da una curva regolare (la tangente esiste)
semplice (non ci sono intersezioni) chiusa C. In particolare, questo dignifica che
la regione di piano R racchiusa da C è semplicemente connessa. Allora
I
I
I
H(z)dz =
H • T ds + i H • N ds
C
C
C
I due integrali a secondo membro li conoscete: il primo è la circuitazione di H
lungo la curva chiusa C,
I
ZZ
C (H, C) =
H • dr =
∇ × H dS ,
C
R
(per la seconda uguaglianza è stato usato il teorema di Green-Stokes), mentre il
secondo è il flusso di H attraverso la curva chiusa C (siamo in due dimensioni e il
3
bordo di una regione è una curva chiusa)
I
ZZ
H • N ds =
∇ • H dS ,
F(H, C) =
C
R
per la seconda uguaglianza è stato usato il teorema di Gauss in due dimensioni).
In definitiva,
I
H(z)dz = C (H, C) + iF (H, C)
C
Siete cosı̀ in grado di calcolare integrali di funzione complesse lungo curve chiuse
con metodi che già conoscete: basta che calcolate circuitazione e flusso del campo
coniugato.
Ripasso su curve e convenzioni. Esempio di una regione R del piano semplicemente connessa:
Il bordo è una curva semplice.
connesse:
Esempi di regioni del piano molteplicemente
Il bordo sono due o più curve semplici: C = C1 ∪ C2 ∪ . . ..
Ricordiamo la convenzione sul percorso di un cammino chiuso: si dice
che il bordo C di una regione R è percorso in senso o verso positivo se camminando
lungo quella direzione, la regione risulta sempre a sinistra. Per un cerchio la
direzione positiva risulta essere quella anti-oraria. La normale N è la normale
4
diretta verso l’esterno, e quindi a destra di chi cammina lungo C.
Occorre fare attenzione a questo in particolare per situazioni come nella figura
sopra.
Esempio. Calcoliamo
I
z̄dz
C
per C curva chiusa attorno all’origine, ad esempio un cerchio. Il campo coniugato
associato a H(z) = z̄ è H(r) = r.
La circuitazione è chiaramente zero, ma il flusso è positivo (entrano più linee di
forza, di quante ne escano). In effetti, si ha
∇×r = 0
∇•r = 2
Quindi
I
z̄dz = 2iA
C
dove A è l’area della regione di piano racchiusa da C.
5
4.2.4. Funzioni analitiche = campi solenoidali e irrotazionali nel piano.
Proposizione 4.2.1. Il campo vettoriale coniugato della funzione complessa H è
solenoidale (divergenza = zero) e irrotazionale (rotore = zero) sse H è analitica.
Questa proposizione è molto importante e la sua verifica è un semplice calcolo:
∇ × H = ∂x (−v) − ∂y u = −(∂x v + ∂y u)
∇ • H = ∂x u + ∂y (−v) =
∂x u − ∂y v
Quindi, divergenza e rotore si annullano se e solo se sono soddisfatte le equazioni
di Cauchy-Riemann.
4.2.5. Significato fisico delle funzione analitiche.
• Elettrostatica. Si può pensare al campo coniugato come ad un campo elettritico
E nel piano in condizioni statiche. In questo caso le equazioni sono
∇ × E = 0 ovunque
∇ • E = 0 dove non ci sono cariche
Al campo elettrico E = (Ex , Ey ) è quindi associata la funzione analitica f (z) =
Ex − iEy . La legge di Gauss dice
I
X
E • N ds = 2π
qi
F (E, C) =
C
i
La scelta di 2π a secondo membro è per avere
q
er
r
come campo prodotto da una carica puntiforme q. Notare che nel piano il campo
va come 1/r e non come 1/r2 . Fisicamente possiamo pensarlo come ottenuto da
un filo indefinito normale al piano con densità lineare di carica uniforme. Le linee
di forza del campo sono ben note:
Il campo E nel piano è il campo elettrico in un piano normale al filo. La funzione
complessa coniugata associata al campo di una carica puntiforme nell’orgine è
q
e−iθ
=q
z
r
6
Vediamo un problemino che ci sarà utile tra poco. Se nel piano ci sono altre
cariche, per il campo elettrico totale avremo
q
E = er + E ext
r
dove E ext è il campo generato dalle cariche esterne.
associata a E ext , la funzione complessa associata a E è
Detta g(z) la funzione
q + zg(z)
q
+ g(z) =
z
z
Se prendiamo una curva C che racchiude solo l’origine, per la legge di Gauss
abbiamo
I
F (E, C) =
E • N ds = 2πq
C
In generale
I
H(z)dz = C (H, C) + iF (H, C)
C
ma nel nostro caso la circuitazione C è zero. Quindi
I
q + zg(z)
dz = 2πiq
z
C
Tra poco ritorneremo a questa formula carina.
• Magnetostatica. Equazioni per il campo magnetico:
∇ × B = 0 dove non ci sono correnti
∇ • B = 0 ovunque (non ci sono cariche magnetiche)
Possiamo procedere come prima, ma adesso i ruoli di circuitazione e flusso si
scambiano: abbiamo cariche di “circuitazione” cioè correnti I e le linee di flusso
prive di pozzi e sorgenti:
7
• Fluido perfetto stazionario. Equazioni per il campo di velocità del fluido:
∇×V
∇•V
= 0 dove non ci sono vortici
= 0 dove non ci sono pozzi o sorgenti
Per “cariche” (pozzi o sorgenti e vortici) puntiformi, oltre alle linee di flusso già
viste per campi elettrici e magnetici, adesso sono anche possibili configurazioni di
questo tipo
Il punto è sia una sorgente sia un vortice.
4.2.6. Teorema di Cauchy.
Proposizione 4.2.2. Sia f (z) analitica in una regione R e sul suo bordo C. Allora
I
f (z)dz = 0
C
La dimostrazione segue da quanto visto finora.
4.2.7. Formula di Cauchy. Riprendiamo la formula “carina” che avevamo ottenuto parlando di elettrostatica,
I
q + zg(z)
dz = 2πiq
z
C
g(z) è analitica, per il resto è arbitraria. Quindi quello che abbiamo a numeratore
della funzione integranda è una funzione analitica f (z) nella regione racchiusa da
C tale che f (0) = q, che è la quantità che compare a secondo membro moltiplicata
per 2πi. Quindi, facendo astrazione dal significato fisico, quello che abbiamo è
I
f (z)dz
= 2πif (0)
z
C
Aver posto la carica nell’origine era del tutto arbitrario, l’avessimo posta in un
generico punto p avremmo ottenuto
I
f (z)
dz = 2πif (p)
C z −p
Questa formula è nota come formula di Cauchy e vale sotto l’ipotesi che f (z) sia
analitica all’interno e lungo una curva semplice chiusa C; p è un punto qualsiasi
all’interno di C.
8
Il fatto che nel caso considerato q fosse reale è irrilevante: la formula vale per q
complesso. Vista la sua importanza, riotteniamola procedendo direttamente:
Consideriamo la funzione
f (z)
H(z) =
z−p
dove f (z) è analitica. Poiché H(z) è analitica eccetto che in p, rotore e divergenza
del campo coniugato associato H saranno nulli ovunque eccetto che in p. Perciò se
C è un un circuito attorno a p, tutto il flusso e circolazione emanano da un piccolo
intorno di p. Se f (p) = A+iB, in questo piccolo intorno (piccolo a piacere) avremo
1
i
A − iB
=A
−B
H̄ =
z̄ − p̄
z̄ − p̄
z̄ − p̄
cioè H̄ =
Da cui
I
C
f (z)
dz = C (H, C) + iF (H, C) = −2πB + i2πA = 2πif (p)
z−p