Il moto uniformemente accelerato
Quando l' accelerazione rimane costante nel tempo si ha il moto
uniformemente accelerato.
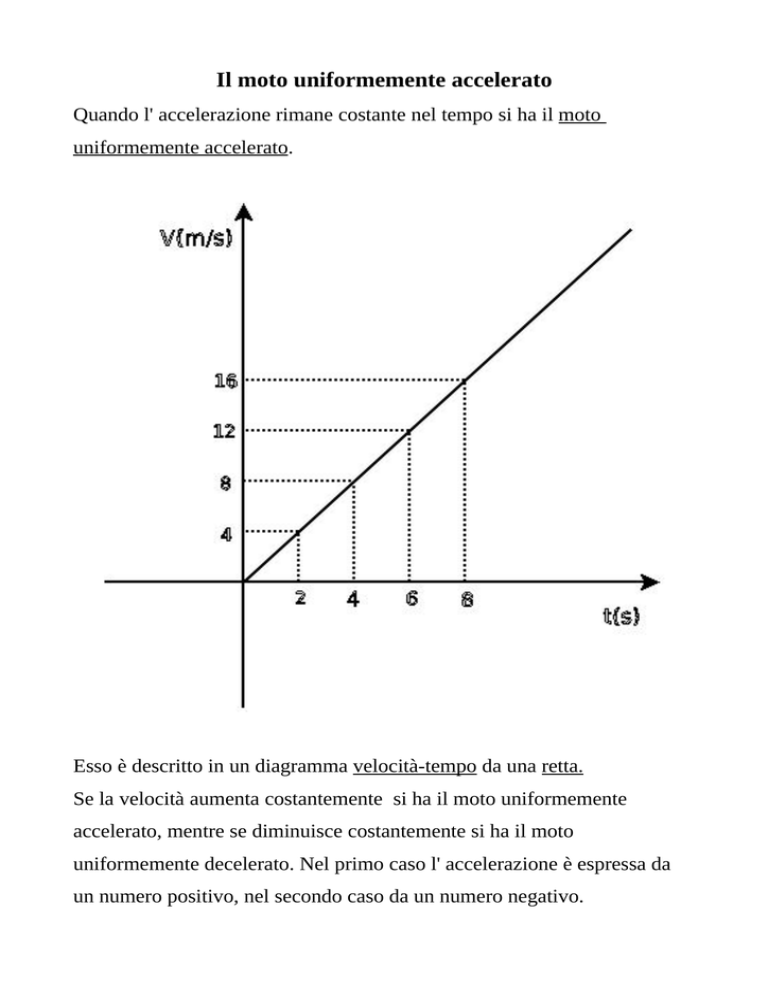
Esso è descritto in un diagramma velocità-tempo da una retta.
Se la velocità aumenta costantemente si ha il moto uniformemente
accelerato, mentre se diminuisce costantemente si ha il moto
uniformemente decelerato. Nel primo caso l' accelerazione è espressa da
un numero positivo, nel secondo caso da un numero negativo.
Verifichiamo la legge oraria del moto rettilineo uniforme calcolandola
graficamente in un diagramma velocità-tempo. È ovvio che un moto
rettilineo uniforme in un diagramma velocità-tempo è descritto da una retta
parallela all' asse dei tempi. Infatti la velocità rimane costante e l'
accelerazione è sempre nulla (essendo nulla la pendenza di una qualsiasi
retta parallela all' asse delle ascisse).
Osserviamo che lo spazio raggiunto all' istante t 1 è uguale all' area del
rettangolo SPRO avente per lati V 1 e t 1 . Quindi all' istante t 1
S =V 1∗t 1
. Dimostrato ciò possiamo affermare che è confermata la legge
generica S =V ∗t .Questo discorso vale anche per il moto uniformemente
accelerato, che può essere anch' esso calcolato graficamente. Supponiamo
di avere il più semplice dei casi, cioè quando t 0 =0 e V 0 =0 :
In questo caso la retta parte dall' origine degli assi, ma è obliqua , per cui
lo spazio è dato dall' area del triangolo OAB. I cateti del triangolo sono V
e t, come si vede dalla figura.
S=
V ∗t
2
V
Ma a= t , quindi V =a∗t . Sostituendo:
S=
a∗t∗t
2
1
S = at2
2
Adesso consideriamo il caso in cui il punto materiale si muove con una
velocità iniziale diversa da zero:
In questo caso lo spazio è uguale all' area del trapezio ADCE, formato dal
rettangolo ABCD e dal triangolo ABE. Indichiamo con S' e S'' le aree
rispettivamente di ABCD e ABE. Quindi otteniamo:
S =S ' S ' '
S ' =V 0 t
1
1
S ' ' = V t = a t2
2
2
1
S =V 0 t a t 2
2
Se avessimo un tempo iniziale t 0 ≠0 con la formula precedente si
otterrebbe la variazione di spazio ΔS :
ΔS =S− S0
1
ΔS =V 0 t a t 2
2
1
S −S 0 =V 0 t a t 2
2
1
S =S 0 V 0 t a t 2
2
Questa è la legge oraria più generica possibile per un moto uniformemente
accelerato.
Adesso proviamo ad analizzare la traiettoria di un moto uniformemente
accelerato in un diagramma spazio-tempo:
Il grafico a prima vista sembrerebbe una parabola.
1 2
Esso è dato dall' equazione S = 2 at
1
Poniamo 2 a=m e t = x .
L' equazione diventa S =mx 2 , che è proprio l' equazione di una parabola
passante per l' origine. Quindi possiamo concludere che il moto
uniformemente accelerato rappresenta in un diagramma spazio-tempo una
parabola.
Infine possiamo dimostrare un po' di formule per svolgere facilmente i
problemi. Proviamo a determinare la velocità e l' accelerazione senza
conoscere il tempo:
V =at
t=
V
a
1
S = at2
2
2
1 v
S= a 2
2 a
2
S=
V
2a
2
V = S∗2a
V = S∗2a
2
V = S∗2a
2a=
V
S
2
2
V
a=
2S
Abbiamo dimostrato che la velocità è data anche da V = S∗2a e la
accelerazione è data anche da
2
V
a=
2S
.











