Lezioni Combustione 2 7 aprile 2009 Abbiamo definito la funzione densità di probabilità (pdf) della componente ux di velocità come:
pdf (ux) =
1 dN u x
N du x
che per il principio di equidistribuzione dell’energia di Boltzmann risulta:
2
mu x
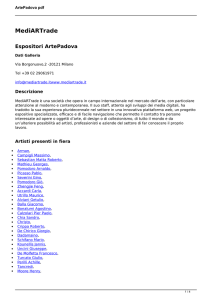
pdf (ux) = A exp () (1)
2kT
1
mux2 rappresenta l’energia cinetica associata alla singola particella e kT l’energia cinetica
2
media di tutte le particelle presenti nel contenitore. Per valutare la costante A è sufficiente integrare
su tutto il campo di velocità la pdf(ux). Si ha:
dove
∫
∞
0
pdf (u x )du x =
∫
∞
0
1 dN ux
du x =
N du x
∫
∞
0
dN ux
N
L’ultimo integrale per definizione di pdf(ux) è unitario, allora:
∫
∞
0
⎛ mu x 2 ⎞
∞
dN ux
⎟
= 1 = A ∫ exp⎜ −
⎜ 2kT ⎟du x
0
N
⎝
⎠
Da cui si ottiene:
1
A=
∫
∞
0
⎛ mu x 2
exp⎜⎜ −
⎝ 2kT
m
l’integrale al denominatore diventa:
2kT
Poniamo a =
∫
∞
0
(
⎞
⎟du x
⎟
⎠
2
)
exp − au x du x
Per risolvere il seguente integrale facciamone il quadrato e poniamo per comodità ux = x. Si
2
∞
∞
∞
ha: ⎛⎜ ∫ exp( − ax 2 )dx ⎞⎟ = ⎛⎜ ∫ exp(−ax 2 )dx ⎞⎟ ⎛⎜ ∫ exp(−ay 2 )dy ⎞⎟ =
⎝ 0
⎠ ⎝ 0
⎠
⎠⎝ 0
Riconduciamo il tutto a coordinate sferiche sapendo che:
r2 = x2 + y2
dx = dy = rdθdr
Si ha:
π
∞
∞
π 1
1π
π ⎛ exp(−ar 2 ) ⎞
2
⎞
2⎛
=
∫0 ⎜⎝ ∫0 exp(−ar )rdr ⎟⎠dϑ 2 ⎜⎜⎝ − 2a ⎟⎟⎠ = 2 2a = 4 a
0
∫
∞
0
exp(−a( x 2 + y 2 ))dxdy
Lezioni Combustione 2 7 aprile 2009 Quello ottenuto è il risultato dell’integrale al quadrate, facendone la radice quadrata si ottiene il
valore desiderato quindi:
f(x) =
1 π
2 a
Allora si ha:
A=
1
1 π
2 a
=
1
1 2πkT
2
m
=
⎛ πkT ⎞
=⎜
⎟
πkT
⎝ 2m ⎠
2m
1
−
1
2
Conoscendo la temperatura T del sistema, k è noto, la massa di una particella m è pari al rapporto
tra il suo peso molecolare e il numero di Avogadro, quindi la costante A in definitiva è nota.
Ponendola nella relazione (1) si ha:
⎛ πkT ⎞
pdf(ux) = ⎜
⎟
⎝ 2m ⎠
−
1
2
2
mu x
exp ()
2kT
Questo andamento è possibile diagrammarlo. Si ha:
pdf(ux) A ux Questo discorso può essere ripetuto anche per uy e uz. Se vogliamo conoscere la probabilità che una
particella abbia una velocità c le cui componenti sono ux e uy dobbiamo eseguire il prodotto tra
pdf(ux) e pdf(uy).
y uy c ux x Lezioni Combustione 2 7 aprile 2009 Si ha:
⎛ πkT ⎞
pdf(c) = pdf(ux) pdf(uy) = ⎜
⎟
⎝ 2m ⎠
−
1
2
mu x ⎛ πkT ⎞
exp ()⎜
⎟
2kT ⎝ 2m ⎠
2
−
1
2
exp (-
mu y
2
)
2kT
utilizzando la definizione di pdf(ux) riscriviamo la realzione di Boltzmann unidimensionale in altro
modo:
1
⎛ mu x 2 ⎞
dN ux ⎛ 2m ⎞ 2
⎜−
⎟
=⎜
exp
⎟
⎜ 2kT ⎟du x
N
⎝ πkT ⎠
⎝
⎠
Vogliamo ora conoscere la probabilità che una particella abbia una velocità assoluta c. Si avrà:
1
1
2
2
⎛ m(u x 2 + u y 2 ) ⎞
mu y
dN c
mu x ⎛ 2m ⎞ 2
⎛ 2m ⎞ 2
⎛ 2m ⎞
⎟du du =
)⎜
)= ⎜
== ⎜
⎟ exp⎜ −
⎟ exp (⎟ exp (⎜
⎟ x y
N
π
kT
2
kT
2
kT
π
kT
π
kT
2
kT
⎝
⎠
⎝
⎠
⎝
⎠
⎝
⎠
⎛ mc 2 ⎞
⎛ 2m ⎞
⎟⎟2πcdc
⎜
⎟ exp⎜⎜ −
⎝ πkT ⎠
⎝ 2kT ⎠
Questa relazione definisce la pdf(c) bidimensionale. Procedendo in maniera analoga si ottiene anche
la relazione nel caso tridimensionale. Si ha:
3
⎛ mc 2 ⎞
dN c ⎛ 2m ⎞ 2
⎜⎜ −
⎟⎟4πc 2 dc
=⎜
exp
⎟
N
⎝ πkT ⎠
⎝ 2kT ⎠
Equazione di Maxwell-Boltzmann
Questa equazione definisce la distribuzione statistica delle particelle aventi velocità assoluta c.
Portando dc al primo membro si ottiene la pdf (c). Infatti:
3
⎛ mc 2 ⎞
1 dN c ⎛ 2m ⎞ 2
pdf (c) =
= ⎜
⎜⎜ −
⎟⎟
exp
⎟
N dc
2
kT
⎝ πkT ⎠
⎝
⎠
Questa relazione è possibile diagrammarla ottenendo una distribuzione di questo tipo:
pdf(c) cm cm2 cm3 cmod c Lezioni Combustione 2 7 aprile 2009 Il valore modale di questa distribuzione definisce il valore di velocità c più probabile cmod.
Valutiamo invece il valore medio cm, il valore quadratico medio cm2 e il valore cubico medio cm3.
Ad esempio si ha:
cm = ∫ pdf (c)cdc =
8kT
πm
Moltiplichiamo e dividiamo per N0. Si ha:
cm =
8kTN 0
πmN 0
Ma kN0 = R0 e mN0 = M si ha allora:
cm =
8R0T
πM
Inoltre R =
cm =
R0
allora:
M
8RT
π
Procedendo in modo analogo per cm2 si ha:
cm = ∫ pdf (c)c 2 dc =
2
3kTN 0
3R0T
3kT
=
=
= 3RT
m
mN 0
M
Si nota come la velocità media mostri affinità nella sua espressione con la velocità del suono.
Infatti:
a = γRT
Velocità del suono
Ciò suggerisce come i valori attinti dalla velocità media siano simili a quelli attinti dalla velocità del
suono.
Lezioni Combustione 2 7 aprile 2009 Valutazione del Cammino Libero Medio Molecolare
Consideriamo delle particelle rigide e chiamiamo d il loro diametro. Visualizziamo un arbitrario
percorso compiuto da questa particella in 1 secondo di tempo.
t=1s
d/2 d/2 Il volume spazzolato da una particella nell’unità di tempo è pari a un cilindro spezzato (tratteggiato
in figura) di altezza pari a c e sezione pari a π d2/4. Allora:
d2
V* = π
c
4
Volume spazzolato da una particella nell’unità di tempo
In realtà siamo interessati a valutare il numero di particelle che la particella in esame incontrerà nel
suo percorso. La particella incontrerà tutte le molecole contenute in un cilindro spezzato di raggio d.
Si ha:
V ' = πd 2 c
Se moltiplichiamo il volume V’ per la densità molecolare ovvero il numero di particelle per unità di
volume N*, si ottiene il numero di particelle che quella in esame ( nel seguito 1) incontrerà
nell’unità di tempo. Ovvero:
Z1 = πd 2 cN *
L’intervallo di tempo tra due urti consecutivi sarà:
tc =
1
Z1
Mentre il cammino libero medio molecolare ovvero ogni quanto spazio si incontra una particella
sarà:
λ=
cm
c
1
m
= 2 m
= 2
= 2
Z1 πd cm N * πd N * πd ρ
Cammino Libero Medio Molecolare
Lezioni Combustione 2 7 aprile 2009 Si nota come λ dipenda dalla pressione poiché a parità di T ρ è funzione della pressione e sarà
linearmente proporzionale all’inverso della pressione. L’espressione ottenuta è approssimata, quella
rigorosa frutto di una analisi della distribuzione statistica della velocità sarà:
λ=
1
2πd 2 N *
Questo discorso ci consente di interpretare la diffusività di massa, di quantità di moto e termica
come:
D=
1
cm λ
2
Espressione della diffusività in funzione di λ