PROBLEMI SUI GAS PERFETTI
a) Disegna il grafico pressione-temperatura di un gas perfetto, sapendo che quando la temperatura è
T0=0°C (fusione del ghiaccio) la pressione è P0=150.000Pa. Quando disegni il grafico tieni conto
dell’esistenza dello zero assoluto! Dal grafico, senza fare calcoli, sei in grado di sapere la
pressione quando la temperatura è T=100°C? E quando essa è T=-50°C? E quando essa è T=350°C (Attento!)?
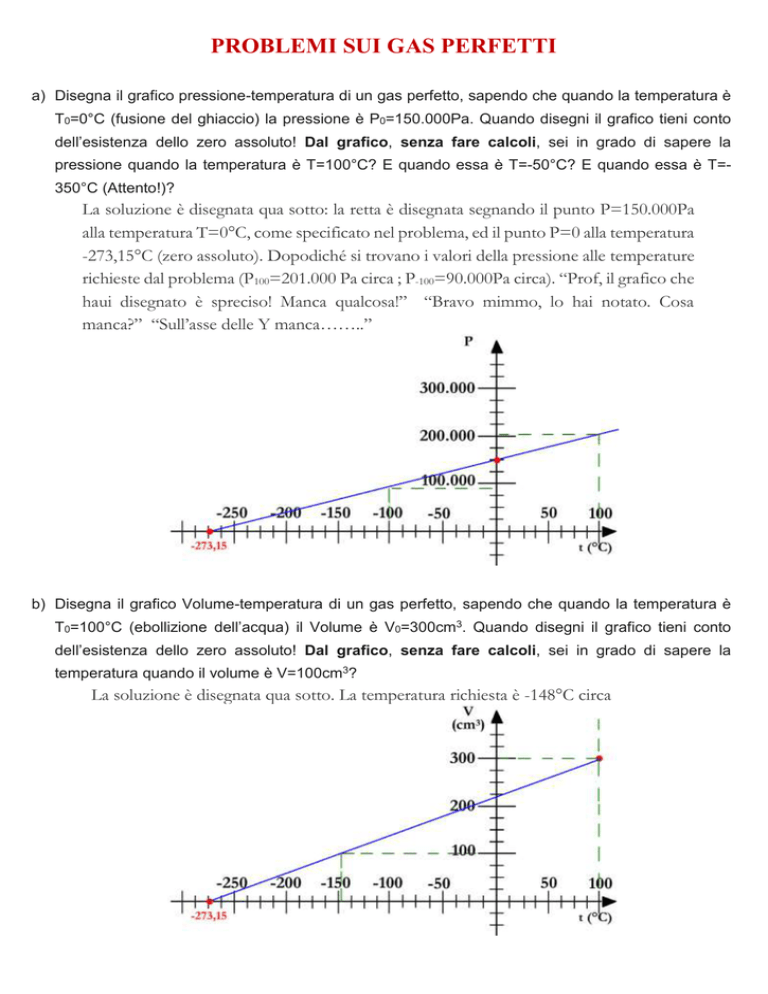
La soluzione è disegnata qua sotto: la retta è disegnata segnando il punto P=150.000Pa
alla temperatura T=0°C, come specificato nel problema, ed il punto P=0 alla temperatura
-273,15°C (zero assoluto). Dopodiché si trovano i valori della pressione alle temperature
richieste dal problema (P100=201.000 Pa circa ; P-100=90.000Pa circa). “Prof, il grafico che
haui disegnato è spreciso! Manca qualcosa!” “Bravo mimmo, lo hai notato. Cosa
manca?” “Sull’asse delle Y manca……..”
b) Disegna il grafico Volume-temperatura di un gas perfetto, sapendo che quando la temperatura è
T0=100°C (ebollizione dell’acqua) il Volume è V0=300cm3. Quando disegni il grafico tieni conto
dell’esistenza dello zero assoluto! Dal grafico, senza fare calcoli, sei in grado di sapere la
temperatura quando il volume è V=100cm3?
La soluzione è disegnata qua sotto. La temperatura richiesta è -148°C circa
Problemi svolti (per semplicità, i problemi pongono lo zero assoluto a -273K e non al reale
valore di -273,15K)
1) 0.5
m3
di un certo gas si trovano sottoposti alla pressione di 2 atm. Calcolare quanti litri occupa il gas,
a temperatura costante, se la pressione viene portata a 5 atm
Poiché la trasformazione avviene a temperatura costante andrà applicata la legge di
Boyle:
p1V1= p2V2 essendo p1 = 2 atm, V1 = 0.5 m3 e p2 = 5 atm. Sostituendo i valori noti nella
legge di Boyle si ha:
2 x 0.5 = 5 V2
Da cui V2 = 2 x 0,5 / 5 =0,2 m3 = 200 dm3 = 200 L
Nota che non è stato necessario trasformare la pressione in Pascal!
2) Una data massa di gas che a 0°C occupa un volume di 10 L ed ha una pressione di 5 atm viene
riscaldato a 150 °C. Calcolare: a) il volume occupato dal gas se si mantiene costante la pressione;
b) la pressione esercitata dal gas se si mantiene costante il volume
a) Applichiamo la prima legge di Gay Lussac: V1/T1= V2/T2 dopo aver operato le
opportune conversioni della temperatura:
T1 = 0°C = 273 K e T2 = 150 + 273 =423 K
Sostituiamo i valori noti nella relazione V1/T1= V2/T2
10 / 273 = V2/ 423
V2 = 10 x 423/ 273 = 15,5 L
b) Applichiamo la seconda legge di Gay Lussac: p1/T1= p2/T2
5/ 273 = p2/ 423
p2 = 5 x 423 / 273 = 7,75 atm
3) 10 L di ossigeno, contenuti in un recipiente a tenuta stagna, hanno, a 0°C, una pressione di 8 atm.
Calcolare la pressione che eserciterà il gas se la temperatura viene portata a – 30°C.
La trasformazione, avvenendo in un recipiente a tenuta stagna, avviene a volume costante
pertanto si deve applicare la seconda legge di Gay Lussac: p1/T1= p2/T2 dopo aver
operato le opportune conversioni della temperatura:
T1 = 0°C = 273 K e T2 = – 30 + 273 = 243 K
Sostituiamo i valori noti nella relazione p1/T1= p2/T2
8 / 273 = p2/ 243
p2 = 8 x 243 / 273 = 7,12 atm
4) Una data massa di gas occupa a 20 °C il volume di 0,05 m3. Calcolare a quale temperatura espressa
in gradi Kelvin occorre portare il gas affinché il volume diventi 100L a pressione costante.
Applichiamo la prima legge di Gay Lussac: V1/T1= V2/T2 dopo aver operato le
opportune conversioni della temperatura e del volume:
T1 = 20 + 273 = 293 K
0,05 m3 = 50 dm3 che corrispondono a 50 L
Sostituiamo i valori noti nella relazione V1/T1= V2/T2
50 / 293 = 100 / T2
T2 = 293 x 100 / 50 =586 K
Poiché il risultato viene chiesto in gradi centigradi T2 = 586 – 273 =313 °C
Nota che abbiamo trasformato i metri cubi in decimetri cubi! Potevamo fare anche
l’opposto, non cambiava nulla.
5) Un gas effettua una trasformazione isoterma passando dallo stato A allo stato B alla temperatura T
= 60,16°C e successivamente un’isobara dallo stato B allo stato C. Calcolare la temperatura nello
stato C, sapendo che PA=400.000 Pa = 4 · 105 Pa, che PB = 150.000Pa = 1,5·105 Pa, VA = 7dm3 e
VC = 10dm3
Applichiamo in sequenza le due trasformazioni, calcolando tutti i parametri degli stati:
1.
Isoterma AB: dello stato finale è nota solo la pressione, per cui ricaviamo il volume
dalla legge di Boyle:
2.
isobara BC: ricaviamo la temperatura finale che permette di contrarre il volume dal
valore VB al valore VC. Applichiamo la prima legge di Gay-Lussac, osservato che TB
= 60,16 + 273 = 333,16◦C:
La temperatura dello stato C è pertanto: TC = 178,4K
6) Quale è il volume occupato da 10g di gas Neon alla temperatura T = 25°C e a pressione ordinaria
(cioè p=1Atm=101.300 Pa; il valore esatto è 1Atm=101.325Pa ma in questo problema si usa il valore
approssimato per semplicità di calcolo), sapendo che la sua massa molare è mmol =
20,18grammi/mole?
Ovviamente T = 25 + 273 = 298K e P = 1Atm = 101.300Pa = 1,013 · 105 Pa. Il volume
del gas si determina con l’equazione di stato, a patto di determinare prima il numero n di
moli. Sapendo che
Si ha che n = 10/20,18 = 0,495moli.
Applicando l’equazione di stato si ha:
7) Una certa quantità di gas perfetto alla temperatura di TA = 400K e alla pressione di PA = 2,5Atm
subisce un’espansione isoterma dallo stato A a quello B in modo che nello stato B il volume sia
doppio. Il gas è quindi compresso isobaricamente sino a tornare al volume di partenza. Determina
la pressione e la temperatura finali del gas. “Prof, ma qual è il volume di partenza? Il testo non lo
dice!” “Mimmo svogliato, stai attento! Sei in grado di risolvere il problema anche senza sapere il
valore iniziale del volume!”
Se la trasformazione AB è isoterma, ovviamente TA = TB e se è VB = 2·VA, allora è anche
(uso la legge di Boyle) .
Se l’ultima trasformazione è isobara, allora
. Sappiamo anche che
l’ultima trasformazione riporta il volume al valore iniziale, per cui VC = VA. Dunque,
applicando la prima legge di Gay-Lussac:
Se il gas contiene tre moli di sostanza, qual è il volume finale del gas?
Il volume di C si trova applicando l’equazione di stato coi valori di TA e PA, oppure con i
valori di TC e PC. Si ha dunque:
8) Una bombola da 20 L contiene azoto (peso molecolare = 28,016 grammi/mole) alla pressione di 100
atm e alla temperatura di 10 °C. Calcola la pressione esercitata dal gas che resta nella bombola
dopo che questa ha erogato 1,5 Kg di azoto se la temperatura non varia.
Il problema va affrontato per gradi: per prima cosa dobbiamo calcolare il numero di moli
iniziali dalla formula: n = pV/RT
Convertiamo la temperatura in gradi Kelvin: T = 10 + 273 = 283 K
Convertiamo la pressione in Pascal: 1Atm=101.325Pa 100atm=10.132.500 Pa
Convertiamo il volume in m3: V=0,02 m3 .
n = 10.132.500 x 0,02/(8,314 x 283) =86,1 = moli iniziali di azoto
Calcoliamo a quante moli corrispondono 1,5 Kg di azoto:
moli di azoto erogate = 1500 g/ 28,016 g/mol = 53,5 moli
Moli di azoto che rimangono nella bombola = 86,1 – 53,5 = 32,6 moli
A questo punto possiamo calcolare la nuova pressione:
p = nRT/V = 32,6 x 8,3146 x 283 K / 0,020 m3 = 3.835.165 Pa = 37,86 atm
Importante! In questo problema è stato necessario usare i Pascal ed i metri cubi perché usiamo la costante R
che è espressa in Pascal ed in m3!
9) Una bombola da 30 L contiene ossigeno (peso molecolare = 32grammi/mole) alla pressione di 150
atm e alla temperatura di 20 °C. Si apre una valvola e si lascia fuoriuscire il gas con regolarità: il
volume del gas rimane perciò costante (è quello della bombola) ed anche la temperatura rimane la
stessa (quando il gas esce essa non cambia). Calcola la massa in Kg di gas che rimane nella
bombola quando la pressione è dimezzata.
Convertiamo la temperatura in gradi Kelvin: T = 20 + 273 = 293 K
Convertiamo la pressione in Pascal: 1Atm=101.325Pa 150atm=15.198.750 Pa
Convertiamo il volume in m3: V=0,03 m3 .
Innanzi tutto calcoliamo le moli di ossigeno inizialmente presenti nella bombola alla
temperatura di 20 °C ovvero di 20 + 273 = 293 K
n = pV/RT = 15.198.750 x 30 / 8,314 x 293 K = 187,2 moli
la massa di ossigeno inizialmente presente è pari a 187,2 mol x 32 g/mol=5990 g
Quando la pressione sarà dimezzata ovvero sarà pari a 150/2 = 75 atm (7.599.375Pa) il
numero di moli sarà pari a:
n = pV/RT = 7.599.375 x 0,03 / 8,314 x 293 =93,6 moli che corrispondono a 93,6 mol x
32 g/mol=2995 g
La massa di ossigeno rimasta nella bombola è pari a 5990 – 2995 =2995 g che
corrispondono a 2,995 Kg
10) Calcola la densità (g/L) di 200grammi di acido solfidrico H2S (peso molecolare= 34,082
grammi/mole) alla pressione di 253.312Pa e alla temperatura di 278 K
La densità () è data dalla formula: =Massa/Volume. La massa è nota: devo trovare il
Volume. Uso l’equazione di stato:
PV = nRT . V = nRT/P . Conosco P, R, T ma non conosco n. La calcolo subito!
n=200g/(34,082g/mol) = … = 3,73 g/L (fai tu i calcoli!)
11) Come cambia la risposta del problema (10) se invece, alla stessa temperatura, pressione e volume,
è presente una mistura di 200g di gas 60% acido solfidrico e 40% Neon (peso molecolare del
Neon: 20,18grammi/mole)?
Devo trovare le moli (n) di 200g di miscela: mmol del gas = 60%34,082g/mol +
40%20,18g/mol = 28,52g/mol.
n = 200g/(28,52g/mol) = 7,01moli
= … 3,13g/L
Problemi presi dai siti:
http://www.chimica-online.it/test/esercizi-gas.htm
http://www.liceoxxvaprile.it/wp-content/uploads/2013/09/Esrcizi1gasperfetti.pdf











