file

CAPITOLO 2
Parallelogrammi e trapezi
1. I PARALLELOGRAMMI CON GEOGEBRA
Esercitazione 1. Costruire un parallelogramma dati tre vertici consecutivi
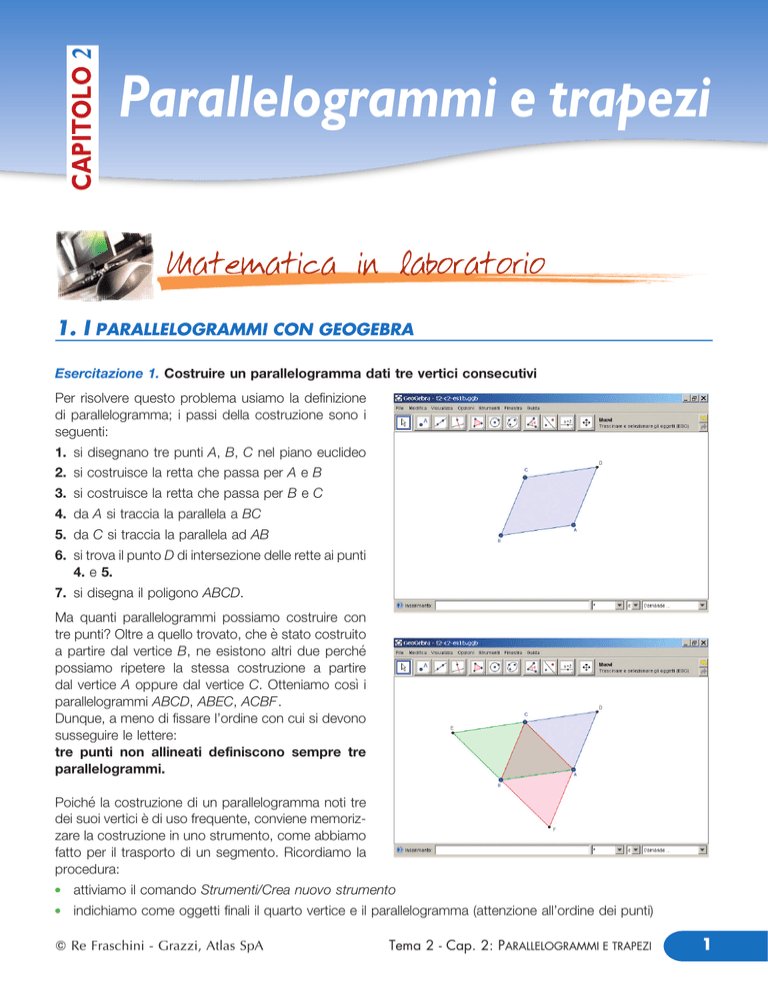
Per risolvere questo problema usiamo la definizione
di parallelogramma; i passi della costruzione sono i
seguenti:
1. si disegnano tre punti A, B, C nel piano euclideo
2. si costruisce la retta che passa per A e B
3. si costruisce la retta che passa per B e C
4. da A si traccia la parallela a BC
5. da C si traccia la parallela ad AB
6. si trova il punto D di intersezione delle rette ai punti
4. e 5.
7. si disegna il poligono ABCD.
Ma quanti parallelogrammi possiamo costruire con
tre punti? Oltre a quello trovato, che eÁ stato costruito
a partire dal vertice B, ne esistono altri due percheÂ
possiamo ripetere la stessa costruzione a partire
dal vertice A oppure dal vertice C. Otteniamo cosõÁ i
parallelogrammi ABCD, ABEC, ACBF.
Dunque, a meno di fissare l'ordine con cui si devono
susseguire le lettere:
tre punti non allineati definiscono sempre tre
parallelogrammi.
Poiche la costruzione di un parallelogramma noti tre
dei suoi vertici eÁ di uso frequente, conviene memorizzare la costruzione in uno strumento, come abbiamo
fatto per il trasporto di un segmento. Ricordiamo la
procedura:
l
attiviamo il comando Strumenti/Crea nuovo strumento
l
indichiamo come oggetti finali il quarto vertice e il parallelogramma (attenzione all'ordine dei punti)
Q Re Fraschini - Grazzi, Atlas SpA
Tema 2 - Cap. 2: PARALLELOGRAMMI E TRAPEZI
1
l
indichiamo come oggetti iniziali i tre punti
l
diamo nome parallelogramma tre vertici allo strumento e salviamo in un file.
Esercitazione 2. Dividere un segmento in n parti congruenti
Dividere un segmento in 2 parti congruenti significa trovare il suo punto medio, dividere in 4 parti significa trovare
il punto medio di ciascuno dei segmenti individuati, dividere in 8 parti significa trovare il punto medio di ciascuno
dei segmenti ottenuti nel caso precedente; in sostanza se n eÁ una potenza di 2 il problema non presenta particolari difficoltaÁ perche si applica piuÁ volte il concetto di punto medio.
Dividere un segmento in un numero di parti che non eÁ una potenza del 2 comporta una procedura diversa che
applica il teorema della corrispondenza di Talete; questa procedura ha comunque carattere generale e si puoÁ
applicare per un n qualsiasi, quindi anche una potenza del 2.
Per eseguirla ci serviremo dello strumento di trasporto dei segmenti che deve quindi essere reso disponibile
aprendo il file corrispondente dal menu File/Apri.
Disegniamo dunque un segmento AB e supponiamo di volerlo dividere in 5 parti congruenti; i passi sono i seguenti:
1. disegniamo un segmento PQ (per questioni di visualizzazione dell'immagine non deve essere troppo lungo);
2. disegniamo una semiretta r avente origine in A;
3. trasportiamo il segmento PQ su r in modo che il primo estremo sia in A;
4. ripetiamo il trasporto altre quattro volte scegliendo come primo estremo ogni volta l'ultimo punto disegnato;
5. dall'ultimo punto ottenuto su r tracciamo la retta s che passa per B;
6. da ciascuno dei punti estremi dei segmenti trasportati tracciamo la parallela alla retta s;
7. determiniamo i punti di intersezione con il segmento AB di ciascuna retta del fascio di parallele
costruito;
8. usando lo strumento 3-Segmento tra due punti
tracciamo i segmenti in cui AB rimane suddiviso
(eventualmente modifichiamo il colore di questi
segmenti per renderli piuÁ visibili).
EÁ adesso possibile verificare con lo strumento 10-Relazione tra due oggetti che i cinque segmenti ottenuti
sono congruenti.
In questa costruzione il segmento AB e la semiretta r
rappresentano le due trasversali del fascio di rette
parallele; avendo disegnato segmenti congruenti su
r, anche quelli individuati sul segmento AB lo sono.
2. I PARALLELOGRAMMI CON CABRI
Un parallelogramma puoÁ essere costruito se si conoscono alcuni elementi; vediamo i casi principali e memorizziamo le costruzioni in una macro in modo da poterle poi utilizzare in altre costruzioni.
Esercitazione 1. Sono noti il centro di simmetria e due vertici consecutivi
Disegna tre punti nel foglio di lavoro e chiama A e B i due vertici, O il centro di simmetria che, come sappiamo, eÁ il
punto di intersezione delle diagonali.
Con lo strumento Simmetria centrale trova adesso i simmetrici dei punti A e B rispetto ad O e, con lo strumen-
2
Tema 2 - Cap. 2: PARALLELOGRAMMI E TRAPEZI
Q Re Fraschini - Grazzi, Atlas SpA
to Poligono dell'icona Rette costruisci il poligono che ha per vertici i punti A e B ed i loro simmetrici (ricorda che
devi chiudere il poligono cliccando alla fine sul primo punto).
Memorizza adesso la costruzione in una macro; ricordiamo la procedura:
l
scegli Oggetti iniziali dall'icona Macro e seleziona i tre punti A, B, O
l
scegli Oggetti finali e seleziona il parallelogramma
l
scegli Definizione della macro e completa la finestra ricordando di inserire il messaggio di aiuto che descrive
la macro nella casella di testo Messaggio di aiuto e di spuntare la casella Salva come file (assegna alla macro il
nome Parallelogramma centro e vertici).
Dopo aver confermato con OK, dai il nome al file e memorizzalo nella libreria.
Esercitazione 2. Sono noti tre vertici
Disegna tre punti nel foglio di lavoro e chiamali A, B, C; per costruire il parallelogramma che li ha come vertici, devi
prima trovare il quarto vertice D. Osserviamo subito che il problema ha piuÁ di una soluzione perche esistono tre
parallelogrammi che hanno vertici nei punti dati (osserva la figura 1); eÁ quindi necessario indicare quale sia l'ordine con cui devono essere presi i punti. Supponiamo che il parallelogramma che dobbiamo disegnare sia ABCD
(gli altri due sono ACBD e BACD); la procedura da seguire eÁ semplice e si basa sulla proprietaÁ dei parallelogrammi di avere i lati opposti paralleli:
l
traccia dapprima le semirette BA e BC
l
traccia da A la parallela r alla semiretta BC
l
traccia da C la parallela s alla semiretta AB
l
trova il punto di intersezione delle due rette r e s e chiamalo D
l
disegna il poligono ABCD.
Memorizza la costruzione in una macro (i tre punti sono gli Oggetti iniziali, il parallelogramma eÁ l'Oggetto finale, dai
nome Parallelogramma tre vertici alla macro).
Ricordati poi che, quando la usi per disegnare un parallelogramma, verranno uniti con dei segmenti il primo punto
con il secondo e il secondo punto con il terzo. Prova dunque a costruire i tre parallelogrammi della figura 1:
l
per disegnare il parallelogramma ABCD indica nell'ordine i punti A, B, C
l
per disegnare il parallelogramma ACBD indica nell'ordine i punti A, C, B
l
per disegnare il parallelogramma BACD indica nell'ordine i punti B, A, C.
Figura 1
ESERCIZI
1. Costruisci un parallelogramma ABCD, prendi un punto S sul lato AB ed un punto T sul lato CD in modo che
AS  CT; verifica che SBTD eÁ un parallelogramma.
Q Re Fraschini - Grazzi, Atlas SpA
Tema 2 - Cap. 2: PARALLELOGRAMMI E TRAPEZI
3
2. Disegna:
a. un rettangolo note le lunghezze dei suoi lati
b. un rombo note le sue diagonali
c. un quadrato nota la lunghezza del suo lato.
3. Disegna un parallelogramma e traccia il segmento che unisce i punti medi di due lati opposti; verifica che
tale segmento eÁ congruente agli altri due lati del parallelogramma.
4. Dopo aver disegnato un parallelogramma, trova il punto O di intersezione delle sue diagonali; verifica che
ogni segmento che passa per O e che ha gli estremi sui lati del parallelogramma ha O come punto medio.
5. Due parallelogrammi hanno un lato in comune e si trovano in semipiani opposti rispetto a tale lato; verifica
che anche il quadrilatero che si ottiene congiungendo i vertici non comuni eÁ un parallelogramma.
6. Dopo aver disegnato un quadrilatero qualsiasi, trova i punti medi dei suoi lati e costruisci il quadrilatero che li
ha come vertici; verifica che tale quadrilatero eÁ un parallelogramma.
7. Dopo aver costruito un rombo:
a. verifica che le sue diagonali sono bisettrici degli angoli;
b. traccia le bisettrici degli angoli formati dalle diagonali e determina i loro punti di intersezione con i lati del
rombo;
c. verifica che tali punti sono i vertici di un quadrato.
8. Disegna:
a. un trapezio qualsiasi
b. un trapezio isoscele e verifica che gli angoli adiacenti alle due basi sono congruenti
c. un trapezio rettangolo.
9. Un segmento AB eÁ la base di un trapezio ABCD, rettangolo in A e D, del quale eÁ data l'ampiezza dell'angolo di vertice B e la misura della base minore CD. Trova una procedura per costruire tale trapezio.
10. Dati tre segmenti, disegna un trapezio isoscele in modo che due di essi siano le basi e il terzo lato sia il lato
obliquo.
11. Disegna un triangolo ABC e prendi un punto P sul lato AC; traccia la retta PM, dove M eÁ il punto medio del
lato BC e indica con Q il punto di intersezione della retta PM con la retta del lato AB. Stabilisci quando il
punto Q esiste e quando non esiste motivando la tua risposta in base alle conoscenze acquisite in questo
capitolo.
12. Disegna un parallelogramma ABCD di centro O e indica con M il punto medio del lato AB e con N il punto
medio del lato CD; trova il punto D 0 simmetrico del vertice D rispetto a M e il punto A 0 simmetrico di A rispetto a N. Verifica che:
a. i punti A 0 , C, B, D 0 sono allineati
b. i punti M, O, N sono allineati
c. i quadrilateri ADBD 0 e ACA 0 D sono parallelogrammi.
13. Costruisci un quadrato e trova una procedura per circoscrivere ad esso un altro quadrato che abbia un lato
parallelo alla diagonale del primo.
14. Disegna un rombo ABCD e dai vertici B e D traccia le rette parallele alla diagonale AC. Sulla parallela per B
prendi due punti P e Q simmetrici rispetto a B e sulla parallela per D due punti simmetrici R e S rispetto a
D.
a. Verifica che il quadrilatero convesso di vertici P, Q, S, R eÁ un trapezio isoscele.
b. Stabilisci come devono essere presi i punti P, Q, S, R in modo che il quadrilatero sia un rettangolo oppure un quadrato.
4
Tema 2 - Cap. 2: PARALLELOGRAMMI E TRAPEZI
Q Re Fraschini - Grazzi, Atlas SpA
1 Un giardino quadrato di 20m di lato viene innaffiato con irrigatori puntiformi. Ciascun irrigatore innaffia
tutti i punti che distano da esso al piuÁ 10 metri. Qual eÁ il minimo numero di irrigatori necessario per innaffiare tutto il giardino?
‰d:Š
a. 1
b. 2
c. 4
d. 4
e. 5
2 In un frutteto rettangolare c'eÁ un albero ogni 4 metri (come in figura). Sapendo
che ci sono 391 alberi, quanto misura il perimetro del rettangolo che ha per
vertici i punti in cui ci sono gli alberi A, B, C, D?
a. 136m
b. 208m
c. 304m
d. 320m
e. non si puoÁ determinare univocamente
‰c:Š
3 Nella figura a fianco i rettangoli (tutti uguali) hanno altezza a e base b. Il perimetro della figura
a. eÁ 15a ‡ 15b
b. eÁ 10a ‡ 10b
c. eÁ 15a ‡ 30b
d. eÁ 30a ‡ 30b
‰b:Š
e. non eÁ nessuno dei precedenti
4 ABCD eÁ un quadrato ed EBC eÁ un triangolo equilatero. Qual eÁ l'ampiezza in
d
gradi dell'angolo AED?
a.
b.
c.
d.
e.
120
135
150
160
nessuno dei precedenti
‰c:Š
d vale 70 e ABCD e DEFG sono quadrati
5 Nella figura l'angolo DCE
d vale:
uguali. L'angolo convesso ADG
a. 110
c. 130
e. 160
b. 120
d. 140
‰d:Š
La parete della camera
Camilla e Leo sono due gemelli; frequentano la stessa scuola, in classi diverse, ma hanno la stessa insegnante di
matematica. E' pomeriggio e da qualche ora Camilla si eÁ chiusa nella sua camera; suo fratello, che si trova nella
stanza a fianco, sente strani rumori e, incuriosito, apre uno spiraglio nella camera di sua sorella.
Q Re Fraschini - Grazzi, Atlas SpA
Tema 2 - Cap. 2: PARALLELOGRAMMI E TRAPEZI
5
Leo:
Camilla:
Leo:
Camilla:
"Camilla, ma che cosa diavolo stai facendo?"
"Ho ridipinto una parete della mia camera usando i teoremi di geometria studiati a scuola".
"Ma sei fuori di testa? Guarda che se vai avanti cosõÁ ti fisso un appuntamento con lo psicologo".
"Ma dai, non sono diventata matta. E' solo che non mi piaceva piuÁ la parete dietro al mio letto tutta
bianca e ho cominciato a tirare qualche riga su un foglio per vedere se mi veniva qualcosa di carino.
Dai vieni a vedere che cosa ho fatto".
Leo apre la porta ed entra in camera senza levare gli occhi dalla parete che gli sta di fronte.
Camilla: "Allora, che cosa ne dici?"
Leo:
"Bello, mi sembra originale. Invece dei soliti fiori, nuvole e farfalle, hai usato dei disegni geometrici,
anche i colori mi piacciono, danno un senso di allegria. Ma che cosa c'entra con i teoremi sui parallelogrammi?"
Camilla: "E' perche tu non guardi mai con attenzione; vieni che ti faccio vedere".
E cosõÁ Camilla comincia a indicare linee e figure e a
spiegare quali teoremi ha usato per costruire quel disegno. Per riuscire a seguire il discorso della nostra
amica dobbiamo mettere delle lettere sul disegno
che riproduce la parete dipinta; osserva allora la figura e giustifica le affermazioni degli esercizi che seguono tenendo presente i teoremi che hai studiato,
ma soprattutto gli esercizi che hai fatto.
1 Osserva i parallelogrammi inscritti nel rettangolo che abbiamo staccato con un tratteggio nella parte in
alto a sinistra della parete; essi hanno tutti lo stesso perimetro.
2 Nello stesso rettangolo la parte centrale in azzurro, che eÁ data dall'intersezione di tutti i parallelogrammi
eÁ un rombo.
3 Nella parte superiore di destra si individuano i triangoli isosceli ABC , BDE, BFG e alcuni parallelogrammi; la caratteristica di questi parallelogrammi eÁ che il loro perimetro eÁ uguale alla somma dei lati congruenti dei triangoli a cui si riferiscono.
4 Il triangolo isoscele ACM ha la caratteristica di avere la base CM che eÁ congruente all'altezza uscente dal
vertice A. Quanto eÁ lungo il lato del quadrato inscritto nel triangolo? Che cosa si ottiene unendo i punti
medi dei lati di questo quadrato?
5 Osserviamo adesso la parte in basso a sinistra relativa al triangolo PQR nel quale PN eÁ la mediana. Il
segmento che esce dal vertice Q e passa per il punto medio di PN interseca il lato PR in un punto S.
Che caratteristiche ha questo punto?
6 Guardiamo da ultimo la parte in basso a destra dove eÁ raffigurato il rombo APRM di centro O; per costruire la figura interna, Camilla ha mandato da O le perpendicolari ai lati del rombo. Che figura ha ottenuto e percheÂ?
5 divide PR in modo che SR  2PS
3 Per esempio DE ‡ AD  AC
6 Un rettangolo, diagonali congruenti di centro O
4 `  1 CM; un altro quadrato
2
2 I vertici dei parallelogrammi sono simmetrici rispetto agli assi di simmetria del rettangolo
1 I lati dei parallelogrammi sono paralleli alle diagonali del rettangolo; i perimetri sono tutti il doppio di una diagonale
6
Tema 2 - Cap. 2: PARALLELOGRAMMI E TRAPEZI
Q Re Fraschini - Grazzi, Atlas SpA