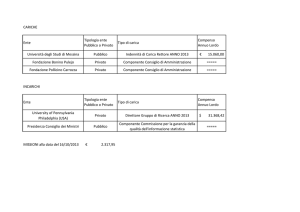
ESERCIZIO 1
Una piccola pallina di massa m è sospesa tramite una cordicella in un campo elettrico uniforme, come
mostrato in figura.
Se la componente x del campo elettrico vale Ex e la componente y vale Ey (Ex ed Ey note), la pallina è in
equilibrio con la cordicella formante un angolo θ.
Trovare la carica della pallina.
[dati: m, Ex, Ey, θ]
Risultato: q=mg/[Ex (cos θ/sen θ)+Ey]
ESERCIZIO 2
Un disco di centro O e raggio R è caricato con una distribuzione di carica superficiale data da:
σ(r) = σ0 (1 - r2/R2)
dove σ0 è una costante e r è la distanza tra il punto considerato e O.
Si valuti in funzione di σ0 ed R la carica totale Q del disco. Si valuti inoltre la densità di carica superficiale
media.
Risultato: Q=π σ0 R2/2; σm = σ0 /2
ESERCIZIO 3
Una particella dotata di carica q e massa m si trova in prossimità di un piano orizzontale carico con densità
di carica uniforme σ, in cui è praticato un foro circolare di raggio R e centro C.
1) Calcolare l’altezza h0 rispetto a C del punto lungo l’asse del foro in cui la particella è in equilibrio;
2) calcolare la differenza di potenziale tra 0 e h0/2.
[Dati: q, m, σ, R]
Risultato: h0 = {R2 / [q σ/(2ε0 m g) ]2 }1/2; V(h0/2) - V(0) = (σ/2ε0) [R – (R2+h02/4)1/2 ]