La diffrazione della luce
CNR-INOA
La luce: onde o particelle?
• C.Huygens (1629-1695)
– Costruisce il più potente telescopio
dell’epoca
– Scopre l’anello di Saturno
– Sostiene la natura ondulatoria della luce
• Basi sperimentali:
– Scarse all’epoca
– Principio di Huygens
• Traité de la lumiére (1690)
• Ogni punto del fronte d’onda può essere
considerato a sua volta sorgente di un’onda
sferica
CNR-INOA
La luce: onde o particelle?
• I.Newton (1642-1727)
– Inventa il primo telescopio a riflessione
– Sostiene la natura corpuscolare della luce
• Lectiones opticae (1669)
• Basi sperimentali:
– La luce si propaga in linea retta
– Gli ostacoli bloccano la luce
– I colori sono composti da particelle di natura diversa
CNR-INOA
Diffrazione della luce
• Diffrazione e Interferenza:
– Per ostacoli opachi estremamante piccoli o
fenditure molto strette (paragonabili a l)
– Crisi del modello corpuscolare
• A.Fresnel (1788-1827)
– Spiega il fenomeno della diffrazione basandosi
sul principio di Huygens (prima della teoria del
c.e.m. di Maxwell)
• Dunque: la luce è costituita da onde!
• Ma anche da particelle!
• La meccanica quantistica metterà d’accordo
i due aspetti (1900)
CNR-INOA
Onde elettromagnetiche
• Il campo elettromagnetico nello spazio libero può
essere rappresentato da un’onda in movimento
con velocità c.
• La lunghezza d’onda e’ caratteristica del tipo di
radiazione:
l
Radiazione
~ 10 m
onde radio
~ 1 cm
microonde
~ 1 mm
infrarosso
~ 600 nm
visibile
~ 200 nm
UV
CNR-INOA
Onde elettromagnetiche
• Campo e.m. che si propaga nello spazio.
• Onda di tipo sinusoidale.
– La propagazione è perpendicolare all’oscillazione
Campo in una dimensione
E x,t
1
0.75
0.5
0.25
x
-6
-4
-2
2
4
6
-0.25
-0.5
-0.75
-1
CNR-INOA
Principio di Huygens
1678 principio di Huygens: la luce consiste di “onde sferiche” di una certa “lunghezza
d’onda l”, tutti i punti di un “fronte d’onda” all’istante t possono essere considerati
centro del nuovo fronte d’onda all’istante t’
“lunghezza d’onda” l
distanza fra due “creste”
“periodicità spaziale”
l
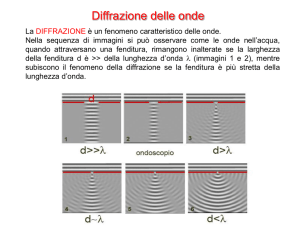
Diffrazione delle onde
Onda piana attraverso una fenditura
d
1
d>>l
4
d~l
2
5
ondoscopio
3
6
d>l
d<l
Diffrazione delle onde
d<<l
Quando d<<l la fenditura si comporta come una sorgente
puntiforme di onde (principio di Huygens)
L’intensità
d>>l
2
4
d~l
5
d>l
3
6
d<l
Notare:
1) Il picco nella 2 è molto stretto, con piccoli lobi ai lati, ma l’intensità è
elevata
2) Il picco si abbassa mano mano che la fenditura si stringe – l’intensità
viene distribuita su un angolo più grande
3) I lobi tendono a scomparire (diffusione da un solo punto)
Effetti di diffrazione
• Qualsiasi tipo di onda
– Onda d’urto in un liquido
– Onda d’urto (acustica) in un gas
– Elettromagnetica
Subisce effetti di diffrazione
Condizione necessaria:
l ~ d (dimensione ostacolo)
CNR-INOA
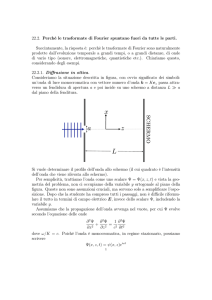
Calcolo dell’intensità
• Ipotesi:
– La luce che arriva sulla fenditura proviene da lontano
(onda piana)
– Lo schermo sul quale visualizziamo l’intensità si trova
lontano dalla fenditura (raggi paralleli)
– l ~ larghezza fenditura d
Principio di Huygens:
Ogni punto è sorgente di onde
CNR-INOA
Differenza di cammino ottico
• A grandi distanze trascuriamo le differenze dovute al diverso angolo di
incidenza sullo schermo
• Consideriamo solo le differenze nel cammino iniziale
• Raggi che provengono dai due lati della fenditura:
• d sinq
d
schermo
q
q
d sinq
CNR-INOA
Differenza di cammino ottico
• Per il principio di Huygens dovremo considerare tutti i punti
interni nalla fenditura come origini di onde
• Raggi che provengono dal centro e da un lato della fenditura:
• Differenza di cammino ottico: (d/2) sinq
schermo
(d/2) sinq
d
q
q
CNR-INOA
Somme su tutti i raggi
• Per ottenere l’intensità sullo schermo dovremo sommare su tutti i raggi,
spostandoci lungo la fenditura
• Raggi che provengono da due punti interni alla fenditura, distanti d/2 :
• Differenza di cammino ottico: (d/2) sinq
schermo
(d/2) sinq
d
q
CNR-INOA
Somme su tutti i raggi
• Per ottenere l’intensità sullo schermo dovremo sommare su tutti i raggi,
spostandoci lungo la fenditura
• Raggi che provengono da due punti interni alla fenditura, distanti d/2 :
• Differenza di cammino ottico: (d/2) sinq
schermo
(d/2) sinq
d
q
CNR-INOA
Interferenza distruttiva
•
•
•
Per ottenere l’intensità sullo schermo dovremo sommare su tutti i raggi, spostandoci lungo la
fenditura
Raggi che provengono da due punti interni alla fenditura, distanti d/2 :
• Differenza di cammino ottico: (d/2) sinq
L’intensità avrà un minimo se la differenza di cammino e’ pari a mezza lunghezza d’onda:
schermo
(d/2) sinq
q
d
(d/2) sinq =l/2
d sinq =l
sinq =l/d
CNR-INOA
Posizione dei minimi
• Raggi che provengono da due punti interni alla fenditura, :
• distanti d/4 - cammino ottico: (d/4) sinq
• distanti d/n – cammino ottico: (d/n) sinq
• In generale: L’intensità avrà minimi per sinq =nl/d
schermo
• d sinq =l, 2l, 3l, 4l.......
n =2
(d/4) sinq
q
d
(d/4) sinq =l/2
d sinq =2l
sinq =2l/d
CNR-INOA
Posizione dei minimi
CNR-INOA
Posizione dei minimi
CNR-INOA
Posizione dei minimi
CNR-INOA
Calcolo analitico dell’intensità
• Applichiamo il principio di Huygens
• Campo nel punto P: somma dei contributi provenienti da tutti
i punti della fenditura
• Contributo di un segmento dy della fenditura:
A
dE cos(t r )dy
r
c
P
r
d
ro
dy
q
y
Calcolo analitico dell’intensità
• Ma r ≈ ro – y sinq dove ro è la distanza dal punto
medio della fenditura
• Nel denominatore poniamo r ≈ ro
A
dE cos(t ro y sin q)dy
ro
c
c
P
r
d
ro
dy
q
y
Calcolo analitico dell’intensità
• Calcoliamo il campo elettrico derivato da
tutti i raggi, spostandoci lungo la fenditura:
A
E dEi cos(t ro y sin q i )dy
ro
c
c
• Se infittiamo i punti delle somme possiamo
definire l’integrale:
a
E
2
a
2
A
cos(t ro y sin q)dy
ro
c
c
Calcolo analitico dell’intensità
• Il risultato dell’integrale definito è:
E
A
1
a
a
sin(
t
r
sin
q
)
sin(
t
r
sin
q
)
o
o
ro ( / c) sin q
c
2c
c
2c
• Sfruttando l’identità trigonometrica:
sin sin 2 cos
sin
2
2
• otteniamo:
2A
a
E
cos(t ro ) sin( sin q)
ro ( / c) sin q
c
2c
Calcolo analitico dell’intensità
• L’intensità della luce è pari al valor
medio E2 su un periodo:
2A
E 2
ro ( / c) sin q
2
a
cos(
t
r
)
sin(
sin
q
)
o
c
2c
2
• L’integrale sul periodo trasforma il
fattore cos(t-c/r) in una costante.
Calcolo analitico dell’intensità
• Intensità = E2:
1 sin2 ( d / l sin q)
I 2
ro
sin2 q
• Ovvero
2
sin x
I Io 2
x
• con
x d / l senq
Grafico dell’intensità sullo schermo
Sin x 2
x 2
1
0.8
0.6
0.4
0.2
x Pi
-3
-2
-1
1
2
3
2
sin x
f ( x) 2
x
CNR-INOA
Posizione dei minimi
• La funzione
2
sin x
f ( x) 2
x
• Ha minimi per x= ±, ± 2, ± 3...
• Ovvero essendo
x d / l senq
• per
l
l
l
sin ,2 ,3 .....
d
d
d
CNR-INOA
Posizione dei minimi
0.05
Sin x d 2
0.5
d
0.0913043
x d 2
0.2
0.2
0.1
0.1
-5
-10
-5
5
d
x d 2
0.3
0.3
0.380435
Sin x d 2
0.5
0.4
0.4
-10
d
Sin x d 2
0.5
10
x
-10
x d 2
-5
1. d
5
Sin x d 2
0.5
0.4
0.4
0.3
0.3
0.2
0.2
0.1
0.1
5
10
x
-10
-5
l
l
l
sin ,2 ,3 .....
d
d
d
10
x
x d 2
5
10
x
CNR-INOA
Posizione dei minimi
• Visualizzazione della distribuzione dell’intensità
della luce su uno schermo
Distribuzione dell’intensità della luce diffratta
Intensità
Ordini
massima
superiori
senq
Schermo
CNR-INOA