LEZIONE : Onde e diffrazione
prof. Fabrizio Bobba
La luce: onde o particelle?
• I.Newton (1642-1727)
– Inventa il primo telescopio a riflessione
– Sostiene la natura corpuscolare della luce
• Lectiones opticae (1669)
• Osservazioni sperimentali:
– La luce si propaga in linea retta
– Gli ostacoli bloccano la luce
– I colori sono composti da particelle di natura diversa
La luce: onde o particelle?
• C.Huygens (1629-1695)
– Costruisce il più potente telescopio dell’epoca
– Scopre l’anello di Saturno
– Sostiene la natura ondulatoria della luce
• Osservazioni sperimentali:
– Scarse all’epoca
–
– Principio di Huygens
• Traité de la lumiére (1690)
• Ogni punto del fronte d’onda può essere considerato a sua
volta sorgente di un’onda sferica
Onde sinusoidali
cresta
t fisso
onda sinusoidale:
singoli punti oscillano come
oscillatori armonici semplici
Lunghezza d’onda
l
Periodo
T
Frequenza
f= 1/ T
Velocità
Ampiezza A
v= l / T
x fisso
Produzione di onda sinusoidale
La quantità
viene detta angolo di fase dell’onda
Sovrapposizione di onde
Principio di
sovrapposizione
Se due o più onde che si
propagano in un mezzo si
combinano in un punto dello
spazio, lo spostamento risultante
è la somma degli spostamenti
dovuti alle singole onde
Sovrapposizione di due onde sinusoidali uguali ma con una differenza di fase
interferenza
costruttiva
interferenza
distruttiva
interferenza
normale
Principio di Huygens
La propagazione dei fronti d’onda (superfici a fase costante) può
essere ottenuta considerando ad un dato istante i punti del fronte
d’onda come le sorgenti di onde sferiche che sovrapponendosi
creando i fronti dell’onda ad istanti successivi.
Diffrazione e Interferenza della luce:
A.Fresnel (1788-1827)
Per ostacoli opachi estremamante piccoli o fenditure molto strette (paragonabili a λ)
il fenomeno della diffrazione si può spiegare con il principio di Huygens
– Crisi ! Crisi del modello corpuscolare
–
–
–
–
Newton:
La luce è composta da particelle (colorate)
fine 1600
Huyghens : La luce è un fenomeno ondulatorio
Fresnel : Ma è evidente : la luce è costituita da onde !
Inizio 1800
Einstein: Si vabbè pero’… a volte la luce si comporta come costituita da
particelle! (eff. fotoelettrico)
Inizio 1900
Ma insomma !! che caspita ….
–
La meccanica quantistica metterà d’accordo i due contendenti
: Hanno tutti ragione !!!
Il fenomeno della diffrazione
Vediamo cosa succede quando facciamo passare un’onda (piana) attraverso una fenditura
d
d>>l
d~l
d=l
d<l
Quando d<l la fenditura si comporta come una sorgente
puntiforme di onde (principio di Huygens)
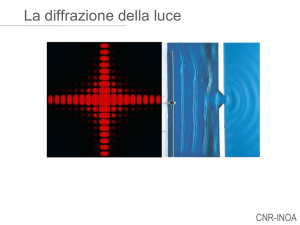
Diffrazione della luce
Frange
Sorgente
Intensità della luce
Schermo
Fenditura / Ostacolo
2
Intensità della luce I A
d>l
1)
2)
3)
d~l
Il picco nella 2 è molto stretto, con piccoli lobi ai lati, ma l’intensità è elevata
Il picco si abbassa mano mano che la fenditura si stringe – l’intensità viene distribuita
su un angolo più grande
I lobi tendono a scomparire (diffusione da un solo punto)
Diffrazione : Qualsiasi tipo di onda ?? YES
– Onda acustica
C’e’ qualcuno che ha un diapason ??
– Elettromagnetica
– Particelle (elettroni, neutroni,…) ??
Esperimento vs. Teoria
–
Rispetto all’esperimento la trattazione fisica della diffrazione è corretta e
completa se:
–
la luce che arriva sulla fenditura è una onda piana (o deve provenire da
molto lontano)
–
Lo schermo sul quale visualizziamo l’intensità si trova lontano dalla fenditura
(raggi paralleli)
–
l ~ larghezza fenditura d
Principio di Huygens:
Ogni punto è sorgente di onde
Differenza di cammino ottico
•
A grandi distanze trascuriamo le differenze dovute al diverso angolo di
incidenza sullo schermo
Raggi che provengono dai due lati della fenditura:
Differenza di cammino ottico = d*sinq
P(q)
r1
d
schermo
r2
q
q
d*sinq
D
Differenza di cammino ottico
•
•
Per il principio di Huygens dovremo considerare tutti i punti interni nalla
fenditura come origini di onde
Raggi che provengono dal centro e da un lato della fenditura:
Differenza di cammino ottico = (d/2) * sinq
(d/2) sinq
q
d
q
D
Somme su tutti i raggi
•
•
Per ottenere l’intensità sullo schermo dovremo sommare su tutti i raggi,
spostandoci lungo la fenditura
Raggi che provengono da due punti interni alla fenditura, distanti d/2 hanno
Differenza di cammino ottico = (d/2) *sinq
schermo
(d/2) sinq
q
d
D
Somme su tutti i raggi
•
•
Per ottenere l’intensità sullo schermo dovremo sommare su tutti i raggi,
spostandoci lungo la fenditura
Raggi che provengono da due punti interni alla fenditura, distanti d/2 hanno
una
Differenza di cammino ottico = (d/2) * sinq
schermo
(d/2) sinq
q
d
D
Buio = Interferenza distruttiva = Intensità minima
•
Differenza di cammino ottico = (d/2) * sinq
•
L’intensità avrà un minimo se la differenza di cammino e’ pari a mezza
lunghezza d’onda:
(d/2) sinq =l/2
d sinq =l
sinq =l/d
(d/2) sinq
d
q
D
n =1
Posizione dei minimi
•
Raggi che provengono da due punti interni alla fenditura, :
• distanti d/4 - cammino ottico: (d/4) sinq
• distanti d/n – cammino ottico: (d/n) sinq
(d/4) sinq =l/2
sinq =2l/d
d sinq =2l
n =2
• In generale: l’intensità della luce sarà minima (buio) quando
sin(q) =nl/d
cioè quando
sinq =l/d, 2l/d, 3l/d, 4l/d.......
(d/4) sinq
d
q
D
Ultime osservazioni
Luce = Onde elettromagnetiche
•
•
Il campo elettromagnetico nello spazio libero può essere rappresentato da un’onda in
movimento con velocità c 300000 Km/sec.
La lunghezza d’onda e’ caratteristica del tipo di radiazione
Spettro delle onde
elettromagnetiche
Raggi X e Raggi
1896 - Roentgen scopre i raggi X.
1914 - Rutherford identifica i raggi
I raggi X sono prodotti nelle transizioni elettroniche
negli atomi di elettroni delle orbite interne.
I raggi sono prodotti nelle reazioni nucleari.
Prima di iniziare l’esperimento
Il principio di Babinet afferma che la figura di
diffrazione prodotta da un corpo opaco (ostacolo) è
identica
a
quella
prodotta
da
un'apertura
"complementare" con la stessa forma e dimensione.
Quanto finora detto per le fenditure vale altresì per gli
ostacoli. Noi useremo un filo sottile o eventualmente un
capello per il nostro esperimento
Materiali e strumenti
• Banco ottico con
sorgente di luce laser
• Metro millimetrato
• Carta millimetrata
• Righello o Calibro
• fili di rame sottili di
dimensioni diverse e
capelli (vostri)
MODO DI OPERARE
CONDIZIONI:
• Ambiente preferibilmente buio
• Allineamento accurato tra fenditure e schermo
• MAI il laser negli occhi, attenti anche alle possibili riflessioni
Ecco ciò che, in varie condizioni sperimentali, si deve vedere
sullo schermo:
Misura dello spessore di un ostacolo
mediante diffrazione
N° Ordine
Misura dello spessore d di un ostacolo
a)
Si punti il Laser in modo tale che intercetti il capello. Si osservi la figura di diffrazione (FD) che si forma su di uno
schermo, posto a distanza D dal capello. La distanza D verrà misurata con un metro a rullino. Una grande distanza
aiuta a ridurre gli errori. La distanza laser-capello non è critica, tuttavia conviene che sia piccola. Si regoli la posizione
del capello e del LASER in modo da ottenere una FD di aspetto simmetrico rispetto al suo centro.
b)
Si segni a matita sul foglio di carta millimetrata dello schermo le frange buie e se ne misuri la posizione lateraleY
Le frange sono numerate dal numero intero n= 1,2,3…... (n° d’ordine)
c)
Si calcoli d, spessore del capello, utilizzando la formula 5, o la 3 tramite una regressione lineare
1) sin qn =n λ /d
r1
L’ angolo θ è legato a D e y dalla relazione:
2) tanqn = yn /D
d
da cui, essendo per angoli piccoli sin() tan(),
3) yn = (λ /d*D)*n n=1,2,3,4,5……
r2
q
q
D
!
Inoltre
4) Δyn = yn+1-yn = λ*D/d cioe’ (Δy1 = y2-y1 , Δy2 = y3-y2 …….)
da cui
5 ) d = λ D/Δy
!
La lunghezza d’onda del LASER che useremo è
λ
= 630 nm, corrispondente a luce di colore rosso
y
Realizzare una tabella dei valori delle misure. Tab1
N° ordine
m
Posizione dei minimi
ym (mm)
1
2
3
4
5
Λ =630 nm, cioè 0.630 µm, o se volete 0.000630 mm
1) Per valutare Ym , misurate la distanza tra Ym e Y-m poi dividete per due. Esempio Y1 = (Y1 , Y-1) / 2,
strumento righello oppure se ritenete di aver un buon allineamento con la quadrettatura millimetrata
dello schermo leggete direttamente sulla carta. Se volete potete usare un calibro.
2) Calcolare il coefficiente angolare (m*λ /d) della retta che meglio approssima i valori sperimentali
graficati su un foglio, o tramite computer (Excel va bene allo scopo).
3) Ricavate dal coefficiente angolare lo spessore dell’ostacolo d e riportatelo come risultato
dell’esperimento
Distanza schermo-ostacolo
D (cm)
Realizzare una tabella di valori delle misure. Tab2
D (cm)
Distanza schermo-ostacolo
Δy1 (mm)
distanza tra il primo ed il
secondo minimo
d (µm)
diametro capello
misura 1
misura 2
misura 3
misura 4
.........
1) Misurate D con il metro a rullo almeno 9 volte (magari da persone diverse) e assumete come valore di D la media aritmetica.
Riportate questo singolo valore in tabella. (se volete potete aggiungere una tabella con le varie misurazioni di D)
2) Misurate Δy1 e riportatene i valori in tabella. Di volta in volta, tra le misure successive, ri-registrate l’allineamento Laser-Ostacolo
(e cancellate di volta in volta i segni a matita sul foglio millimetrato)
Calcolate il valor medio di
d e riportatelo come risultato dell’esperimento
•
Buon Lavoro
• Tempo medio necessario 1 ora.
• Tempo a disposizione 2 ore.