Dinamica
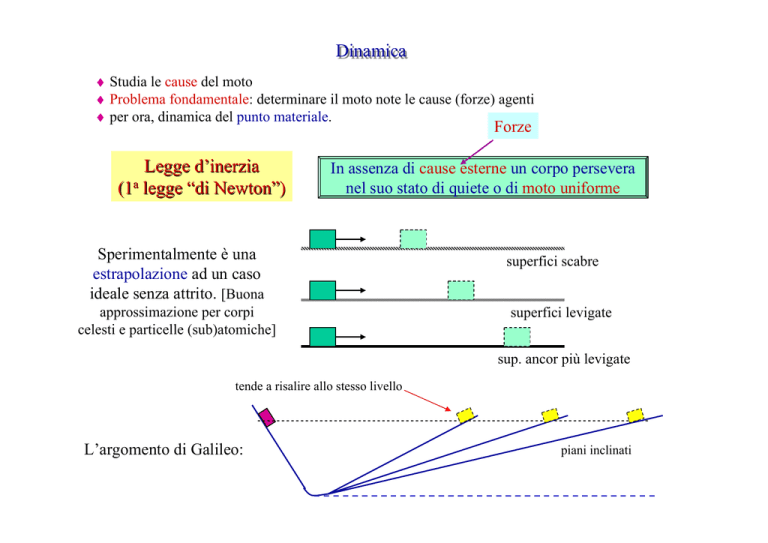
♦ Studia le cause del moto
♦ Problema fondamentale: determinare il moto note le cause (forze) agenti
♦ per ora, dinamica del punto materiale.
Forze
Legge d’inerzia
(1a legge “di Newton”)
In assenza di cause esterne un corpo persevera
nel suo stato di quiete o di moto uniforme
Sperimentalmente è una
estrapolazione ad un caso
ideale senza attrito. [Buona
approssimazione per corpi
celesti e particelle (sub)atomiche]
superfici scabre
superfici levigate
sup. ancor più levigate
tende a risalire allo stesso livello
L’argomento di Galileo:
piani inclinati
1a Legge “di Newton” (Legge d’inerzia)
r
Se il moto non è rettilineo uniforme ( a ≠ 0 ) allora deve agire una forza. Esempi:
Moto rettilineo non uniforme
Caduta dei gravi:
|a|=g=9.8m/s2
v
a
Moto non rettilineo
v2
aN =
≠0
R
Difficoltà: moto e quiete sono sempre relativi: dipendono dal sistema di riferimento
Un sistema di riferimento in cui vale la legge d’inerzia si dice Sistema Inerziale
Esiste? Come si sa che un sistema è inerziale?
Se sappiamo che un corpo non è soggetto a forze e osserviamo a=0 (es. nello spazio interstellare)
Come sappiamo che non agiscono forze?
• Sistema solidale con la distribuzione di massa “media” dell’universo In pratica si
utilizza la radiazione cosmica di fondo.
fondo vS = 369 ± 2 km / s
• Anche la Terra può andar bene in pratica (moti limitati nel tempo e nello spazio,
accelerazioni >> ω2RT=0.034 m/s2 ....)
Enunciazione alternativa della 1a Legge: Esiste almeno un sistema inerziale
inoltre un sistema in moto rettilineo uniforme rispetto ad un sist. inerziale è inerziale (v. moti relativi)
Forza
Serve una definizione preliminare operativa di Forza
•
∆x
•
∆x’
Si può prendere il peso di un certo corpo
come campione di forza
Una molla consente di confrontare le forze
F = F0
2 oggetti identici: ∆x’=2∆x
∆x
∆x0
per una molla ideale.
Comunque basta calibrare
Modulo o intensità di una forza qualsiasi.
Dinamometro
F
La forza è una grandezza vettoriale
(Non è una grandezza fondamentale.
La definizione S.I. si vedrà più avanti)
Nota: non esistono forze in astratto: ogni forza è dovuta a interazione fra sistemi fisici
se su un corpo agisce una forza, dev’esserci un altro corpo che agisce su di esso.
Massa
Applicazione di una forza costante ad un corpo libero
(su piano orizzontale privo di attrito).
Oss. sperimentale: moto uniformemente accelerato
dinamometro
F
F
F1
F
= 2 = ... = N = m
a1
a2
aN
piano senza attrito
massa inerziale
del corpo
la massa è una costante che dipende solo dal corpo
B
A
F
F
F1
F
= 2 = ... = N = m A
a A1 a A 2
a AN
Forze applicate ad A
F
F1
F
= 2 = ... = N = m B
a B1 a B 2
a BN
Forze applicate a B
F
F1 F2
=
= ... = N = mA+ B = mA + mB Forze applicate ad A+B
a1 a2
aN
La massa è una grandezza scalare >0. Additiva. Grandezza fondamentale.
Dall’unità di massa si costruisce anche l’unità di forza.
Una forza di 1N imprime
a=1m/s2
a m=1kg
[m ] = kg
[F ] = kg
m
=N
2
s
2aa Legge di Newton
r
F = ma
Dalle esperienze precedenti risulta:
Legge fondamentale della dinamica
m
Legge vettoriale.
F
a: direzione e verso di F
F: forza totale o risultante
FTOT=R
F1
F1
F2
F2
r
r
R = ma
⎧ F X = ma X
⎪
⎨ F Y = ma Y
⎪
⎩ F Z = ma Z
a1=F1/m
aTOT=R/m
a2=F2/m
r
r
F
r r
r F
a = 1 + 2 = a1 + a 2
m m
2aa Legge di Newton
Equazione del moto
r
dv
F =m
dt
F =m
r
d 2r
nota F(t) o F(r) (più condizioni iniziali)
si può ricavare v(t) o r(t)
dt 2
E’ il problema generale della dinamica.
Strategia per la risoluzione dei problemi: individuare le forze agenti e applicare la 2a legge.
Nota la legge oraria r(t), v(t) per il punto materiale di
massa m consente di ricavare la forza totale agente sulla
Misura dinamica della forza
v2
r r
r
a = aT + aC con aC =
R
r r
r
F = FT + FC
⇒
v
R
FC
Es: in un moto circolare uniforme la forza totale
è “centripeta”
v2
FC = maC = m
R
Esempi di misura dinamica della forza
spinta
portanza
Un aereo di massa m decolla con velocità
costante. Determinare la forza totale agente
peso
resistenza aria
r
r
v = cost ⇒ a = 0
r
r
FTOT = ma = 0
Un’auto di massa m ha accelerazione a.
Quanto vale la forza totale agente sull’auto?
Un aereo si muove con moto circolare uniforme su una circonferenza
di raggio R. Detta v la velocità in modulo, determinare la risultante
delle forze agenti.
r r
r
a = aT + a C
v2
aC =
= ω2R
r
r
r
R
⇒ FTOT = FC = maC
aT = 0
FTOT
v2
=m
R
Formulazione integrale della 2a legge di Newton: Teorema dell’impulso
r
r
dv
F =m
dt
r
r
⇒ Fdt = mdv ⇒
Impulso della forza
t2
r
r
∫ Fdt = ∫ mdv
t2
t1
r
I =
t2
∫
t1
[I ] = Ns = kg m
s
r
r
F dt = m ∆ v
t1
r
r
p = mv quantità di moto
[ p ] = kg m = Ns
s
r dpr
F=
dt
Esempio. Moto 1D con forza costante.
r
r
I = ∆p
Ft = m(v − v0 )
cioè
F
v = v0 + t = v0 + at
m
Limitazioni della 2a Legge della dinamica.
sistema inerziale
v << c
La legge vale per forze “reali” solo in un sistema inerziale.
Come si vedrà, si può estendere la legge ad un sistema non inerziale
a patto di includere le “forze apparenti”.
La formulazione vale solo per “velocità non relativistiche”
In Meccanica Relativistica: m =
m
1−
0
v
c
2
r
p =
2
Con questi cambiamenti, la 2a Legge resta valida nella forma:
λ << D
r
m 0v
1−
v
c
2
m0: massa a riposo
2
r
dp
F =
dt
La legge descrive il moto di corpi macroscopici. Cessa di valere nel limite
a livello atomico-molecolare dove si deve usare la meccanica quantistica.
3aa Legge di Newton
(di azione e reazione)
Le forze sono dovute a interazione mutua fra sistemi fisici.
fisici Esistono sempre in coppia.
Le forze della coppia sono fra loro opposte
A
e dirette lungo la congiungente (*)
zattere si muovono
FA
FB
B
zattera immobile
r
r
F A = FB
A
FA
B
A
FA
FB
B
FB
Terra
Luna
Nota: il fatto che FA+FB=0 non significa che non vi siano accelerazioni, anzi. FA e FB agiscono su
corpi diversi
(*) non sempre vero: v. forza magnetica fra cariche in movimento. Si suppone vero in questo corso
3aa Legge della Dinamica
Esempi
Locomozione
terrestre
forza esercitata
sul pavimento
Locomozione
in un fluido
forza agente
sulla persona
aereo o nave ad elica
....
forza agente
sull’auto
forza agente
sull’aereo
forza esercitata
sull’aria
elica
Moto a reazione
non è necessario un mezzo esterno
forza esercitata
sul fondo stradale
Interazioni fondamentali
Tutte le forze sono riconducibili a
4 interazioni fondamentali
Gravitazionali
Interazione fra masse.
Attrattiva, raggio d’azione infinito
Domina la dinamica celeste. Forza peso ecc.
Elettromagnetiche
Interazioni fra cariche elettriche.
Attrattiva o repulsiva, raggio infinito.
Domina interazioni atomiche/molecolari ecc.
Forti
Interazione fra quark. Molto complessa. Corto raggio (<10-15 m)
Domina struttura e interazioni nucleari, dinamica stellare,
primi istanti dell’universo
Deboli
Interazione fra ‘cariche deboli’. Decadimento beta.
Importante nella dinamica stellare.
Tutte le forze nell’esperienza comune hanno natura gravitazionale o elettromagnetica.
Classificazione “pratica” delle forze che saranno trattate nel corso
678
Forze a distanza
Forze di “contatto”
67
Forza elastica
Attrito dinamico
Attrito viscoso/ resistenza del mezzo
Forza muscolare, ....
Reazione normale
Tensione di una fune/filo
Attrito statico
67
678
Forza gravitazionale (f. peso)
Forza elettrostatica
Forza elettromagnetica
Forza di Lorentz
Reazioni vincolari
Tutte le forze di “contatto” sono, in ultima analisi, di natura elettromagnetica.
Nota: le reazioni vincolari sono le forze più difficili da trattare: si possono ricavare
solo analizzando il sistema fisico caso per caso.
Applicazioni.
2° Principio della Dinamica
Equilibrio di un punto materiale (FTOT=0)
Caso di 2 forze:
F1
F2
⎧ F 2 X = − F1 X
⎪⎪
⎨ F 2 Y = − F 1Y
⎪
⎪⎩ F 2 Z = − F 1 Z
Forze opposte
Caso di 3 forze:
F1
⎧ F1 X + F 2 X + F 3 X = 0
⎪⎪
⎨ F 1Y + F 2 Y + F 3 Y = 0
⎪
⎪⎩ F 1 Z + F 2 Z + F 3 Z = 0
F3
F2
Forze sullo stesso piano
T
N
P
P
Forza gravitazionale o Forza peso
Tutti i corpi, in un medesimo luogo, cadono con la stessa accelerazione (nel vuoto)
che sulla Terra vale in media
g = 9 .80665 m s 2
L’indipendenza dell’accelerazione di gravità dalla natura dei corpi è verificata con
alta precisione (il primo fu Newton) e vale anche per l’antimateria.
g
r
r
r
r
Quindi deve agire una Forza peso (o Peso) F = m a = m g = P
forza proporzionale alla massa: la massa di un corpo si può misurare dal suo peso (bilancia)
Dovuto all’interazione fra masse: in pratica fra la massa del corpo e quella della Terra.
g
•
•
•
•
varia leggermente con la latitudine (9.780m/s2 all’equatore, 9.832m/s2 ai poli)
e con l’altezza (a 10km diminuisce del 0.3%, -10% a 345km)
praticamente campo uniforme (devia di 0.5’ alla distanza di 1km)
altre deviazioni locali dovute alla non sfericità della terra
Ovviamente può essere molto diversa su altri pianeti.
Reazione Normale
Forza di contatto. Reazione vincolare.
Piano orizzontale. In questo caso:
r r
r
N + P = ma = 0
N
N = P = mg
P
N
Piano inclinato liscio (cioè senza attrito: per definizione
“che esercita solo forze normali alla superficie”)
PP
PN = mg cosθ
PN
PP = mg sinθ
P
F
N
⎧⎪mgsinθ = max
⎧⎪ax = g sinθ
⇒⎨
⎨
⎪⎩N − mgcosθ = may = 0 ⎪⎩N = mgcosθ
N
N?
Sensazione di peso.
Misura di una bilancia.
P
P
Reaz. Normale in sistema accelerato. Distacco
Forze di Attrito radente. Attrito statico.
N
AS
Forza di contatto. Reazione vincolare.
Il corpo non si muove se F<Flim
F
Flim = µ S mg = µ S N
costante adimensionale dipende
dalle superfici a contatto
mg
Questa reazione del piano è detta attrito statico ed è AS = -F
Flim = µ S (mg + F0 ) = µ S N
AS non dipende dalla superficie d’appoggio
F0
N
N
F
AS
AS
mg
se
F ≤ Flim = µS N
equilibrio
Riassumendo:
se
F > Flim
il corpo scivola
F
mg
r
r
AS = − F
AS ≤ µ S N
Forze di Attrito radente. Attrito statico.
Piano inclinato scabro
y
N
PP
AS
PN
x
P
componente x
componente y
Il blocco inizialmente in quiete rimane in equilibrio?
La strategia è la seguente:
si suppone equilibrio
in questa ipotesi si calcola AS
si verifica se è soddisfatta la condizione di equilibrio
• se sì, il problema è risolto
• se no, il corpo scivola [usare attrito dinamico (v.)]
⎧mg sin θ − AS = max = 0 ⎧ As = mg sin θ
⇒⎨
⎨
−
=
=
N
mg
cos
θ
ma
0
y
⎩ N = mg cos θ
⎩
possibile purché
AS ≤ µ S N ⇒ tan θ ≤ µ S
Condizione di equilibrio
Forze di attrito radente. Attrito dinamico.
Forza di contatto. Reazione vincolare
Che succede se il corpo scivola sulla superficie (ad es. se la forza applicata ha
intensità sufficiente per muovere il corpo) ?
N
AD
AD = µ D N
F
Anche in movimento agisce una forza che
si oppone al moto: l’attrito dinamico.
mg
direzione e verso: opposto al moto (cioè alla velocità)
Note:
• l’attrito dinamico ha modulo, proporzionale ad N
• µ D ≤ µ S in genere
Fisicamente, l’attrito radente è un fenomeno complesso: interazioni a livello microscopico (es.
nanosaldature al contatto). Le formule date rappresentano una schematizzazione del problema.
Tensione di un filo / fune ideale
Forza di contatto. Reazione vincolare.
Filo/fune ideale:
solo forze lungo il filo (in trazione)
• è perfettamente flessibile
• è inestensibile
• ha massa trascurabile
stessa v, a degli estremi (nella direzione del filo)
stessa tensione (in modulo) in ogni punto
Se la fune è in equilibrio:
T
F
T
T
T
F
la fune esercita agli estremi
una forza opposta a quella applicata.
F
T
L’elemento di fune è soggetto a
forze opposte ai suoi estremi
Tensione di un filo / fune ideale
In pratica, su ogni sezione della fune agiscono forze opposte
Queste conclusioni valgono anche
se il filo non è in equilibrio poiché
la massa è trascurabile
(
Tsx
m≅0
)
r
r
r
T dx + T sx = m a ≅ 0
elemento di filo
Tdx
⇒ T dx = T sx = T
Tensione di un filo / fune ideale
T2
T1
Se la puleggia è senza attrito:
Senza attrito, T ha lo
stesso modulo in ogni
tratto di fune.
r
r
T1 = T 2
T
T
T
F
P
Tratti di filo distinti. Qui le tensioni differiscono. Nell’esempio:
T3
m3
T1
T2
m2
piano liscio
m1
⎧T3 = m3a
⎪
⎨T2 − T3 = m2 a
⎪T − T = m a
1
⎩1 2
⎧T3 = m3 a
⎪
⎨T2 = (m2 + m3 ) a
⎪T = (m + m + m ) a
1
2
3
⎩1
Forza elastica
Forza di richiamo proporzionale allo
spostamento rispetto ad un punto O
r
r
F = − k∆x
costante elastica della molla [k]=N/m
Tipicamente è la forza esercitata da un corpo deformato, per deformazioni piccole e reversibili.
Deformazione elastica.
In genere lo spostamento ∆x si indica con x
(si pone l’origine all’estremo libero, asse x
nel verso della molla)
Es. molla con estremo fisso.
lo
F = − k∆x = − kx
O
P
∆x = l − l o
(legge di Hooke)
dal momento che la molla
è orientata come l’asse x
asse X
∆x
Tratteremo solo molle ideali:
• per cui vale sempre F= -kx
• di massa trascurabile
Esempi di forza centripeta
v
v
R
+
FC
e
R
Forza elettrostatica
Forza gravitazionale
FN
FN
R
P
P
Attrito statico
AS
AS
Curva inclinata. Attrito statico e reazione normale
l
T
R
Pendolo conico. Tensione del filo
P
θ
Forza elastica. Moto armonico
Equazione del moto armonico
⎧ F = −k∆x = −kx
⎪
⎨ d 2x
⎪m 2 = −kx
⎩ dt
la soluzione generale si può scrivere
posto
ω=
k
m
d 2x
⎛k⎞
2
=
−
⎜ ⎟ x = −ω x
2
dt
⎝m⎠
x( t ) = A cos( ω t + ϕ )
Le costanti si determinano dalle condizioni iniziali. Ad es.
⎧⎪x( 0 ) = x0
⎨
⎪⎩v( 0 ) = 0
⇒ x( t ) = x0 cosω t
⎧⎪x( 0 ) = 0
⎨
⎪⎩v( 0 ) = v0
⇒ x( t ) =
v0
ω
sin ω t
il moto armonico è molto importante: è il moto caratteristico delle piccole oscillazioni
intorno alla posizione di equilibrio.
Pendolo semplice.
d 2θ
ml
= − mg sin θ
2
se θ<<1 rad
dt
d 2θ
⎛g⎞
2
=
−
sin
θ
≅
−
ω
θ
⎜
⎟
2
dt
⎝l⎠
θ
mgsinθ
Moto tangente
ma T = FT
mgcosθ
posto
ω =
g
l
T = 2π
l
g
in questa approssimazione il periodo non dipende dall’ampiezza delle oscillazioni.
Moto radiale
v2
T − mg cos θ = ma N = m
l
v2
T = mg cos θ + m
l
la tensione dipende dalla velocità












