Parte 2a

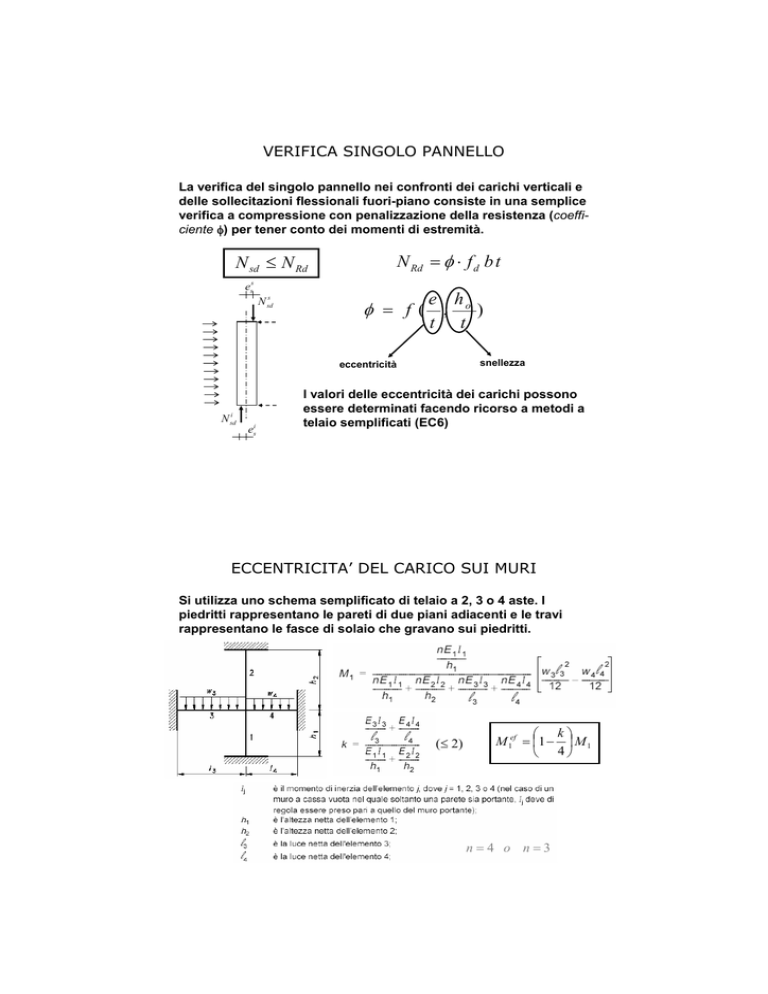
VERIFICA SINGOLO PANNELLO
La verifica del singolo pannello nei confronti dei carichi verticali e
delle sollecitazioni flessionali fuori-piano consiste in una semplice
verifica a compressione con penalizzazione della resistenza (coefficiente φ) per tener conto dei momenti di estremità.
N Rd = φ ⋅ f d b t
N sd ≤ N Rd
ess
N sds
e ho
)
t t
φ = f( ,
snellezza
eccentricità
N sdi
esi
I valori delle eccentricità dei carichi possono
essere determinati facendo ricorso a metodi a
telaio semplificati (EC6)
ECCENTRICITA’ DEL CARICO SUI MURI
Si utilizza uno schema semplificato di telaio a 2, 3 o 4 aste. I
piedritti rappresentano le pareti di due piani adiacenti e le travi
rappresentano le fasce di solaio che gravano sui piedritti.
(≤ 2)
 k
M 1ef = 1 −  M 1
 4
n=4 o n=3
ECCENTRICITA’ DEL CARICO SUI MURI
ECCENTRICITA’ STRUTTURALE
Un altro metodo di calcolo delle eccentricità del carico dei solai si
basa su regole empiriche
d’2 d”2
d2
N2
a
t
N’2
d2 =
t a
−
2 3
N”2
t
t ( N ' − N 2" )
d 2 = ⋅ 2'
3 ( N 2 + N 2" )
L’eccentricità strutturale totale è quindi data dalla relazione
t1
t1
N d + N2 d2
es = 1 1
N1 + N 2
d1 N1
N2= N’2+ N”2
d1 N1
N2
N2
d2
d2
t
t
ECCENTRICITA’ DA CARICO ORIZZONTALE
L’azione orizzontale agente perpendicolarmente al piano medio
della parete produce un momento flettente dal quale si ricava ev
N sds
N sdc
Mv =
h
q h2
8
ev =
Mv
N sdc
q
ECCENTRICITA’ ACCIDENTALE ea
Tiene conto delle tolleranze di verticalità e linearità nella costruzione della parete
ea =
h
200
h altezza di piano in cm
COMBINAZIONE ECCENTRICITA’
EUROCODICE n. 6
Mi+ Mvi
Mvs
Ms
N sds
N sdm
+
q
Mvm
em =
=
N sdi
Mi
Mvi
verticali
orizzontali
esup =
M m M vm
+
+ ea
N sdm N sdm
einf =
Mi
M s M vs
+ s + ea
N sds
N sd
Mi
+ ea
N sdi
totali
DM 9.1.1987
ess
ess
N sds
N sdm
q
h
+
ev
esup = ess + ea
em =
=
esup
2
einf = 0
verticali
orizzontali
totali
+ ev
t
(≤ )
3
t
(≤ )
3
VERIFICA PANNELLO
Sezioni di estremità pannello
φ s ,i = f (
esup,inf
t
, 0) = 1 − 2
N Rd = φs ,i ⋅ f d b t
esup,inf
t
N sd ≤ N Rd
Sezioni centrale del pannello
ho

−2

em ho
em 

t
φm = f ( , ) = 1 − 2  exp −
t t
t 
 23 − 37 em


t

N Rd = φm ⋅ f d b t
(Valori Tabella φ DM 1987)






(Valori Tabella φ DM 1987)
N sd ≤ N Rd
PROCEDURA DI VERIFICA STRUTTURALE
Le fasi operative per la verifica di una costruzione in muratura sono
1. Individuazione della struttura portante e della geometria
2. Determinazione delle caratteristiche meccaniche della muratura
• resistenza caratteristica a compressione fk
• resistenza caratteristica a taglio puro fvko
• resistenze di calcolo
• moduli di elasticità E e G
3. Analisi dei carichi
4. Distribuzione del carico sia verticale che orizzontale sui muri
• distribuzione carichi verticali
• distribuzione forze orizzontali
PROCEDURA DI VERIFICA STRUTTURALE
5. Determinazione sollecitazioni agenti sul muro da verificare
• determinazione sollecitazioni normali N1, N2
• determinazione della sollecitazione orizzontale (in piano, fuoripiano)
• determinazione momento da forze orizzontali (in piano, fuoripiano)
6. Verifica agli sforzi normali
• determinazione eccentricità ea, es, ev, esup, einf, em per le verifiche
• determinazione dei coefficienti φ
• verifica a compressione nelle sezioni di estremità e di mezzeria
• verifica a pressoflessione per azioni orizzontali nel piano
7. Verifica agli sforzi taglianti
• determinazione della tensione di compressione media σn
• determinazione dimensione zona compressa b’
• verifica a taglio
CARATTERISTICHE MECCANICHE MURATURA
Si suppone che l’edificio venga costruito con elementi in laterizio
semipieni con resistenza dei blocchi di fbk = 15 MPa e con malta
cementizia della classe M2 (8 MPa)
Dalla Tabella A del DM 9.1.1987 si ricava per la resistenza a
compressione caratteristica della muratura
f k = 6.7 MPa
La resistenza a taglio in assenza di carichi verticali si ricava dalla
Tabella B dello stesso Decreto
f vko = 0.2 MPa
I valori di calcolo si ricavano dividendo questi valori per γm=3
I valori di E e G risultano
G = 0.4 E = 2680 MPa
E = 1000 f k = 6700 MPa
EC6
fk
fvko
MPa
MPa
5.4
0.2
γm
2÷3
E
G
MPa
MPa
5400
2160
Dipende dalla categoria
di esecuzione e dal
controllo dei materiali
COMPORTAMENTO PER AZIONI SISMICHE
Le strutture in muratura non armata sono particolarmente vulnerabili alle azioni sismiche a causa di
• Ridotta duttilità (limitata capacità di dissipare energia)
• Presenza di sollecitazioni fuori piano nelle pareti
• Rottura per sollecitazioni nel piano di tipo tagliante
Inoltre, la presenza contemporanea di sollecitazioni nel
piano e fuori piano anticipa il collasso
Auspicabile il
ricorso alla
muratura armata
CONFIGURAZIONI STRUTTURALI
I numerosi terremoti occorsi nel passato hanno evidenziato che oltre
alla qualità dei materiali è fondamentale la configurazione strutturale
Gli edifici con forma regolare e con pareti e solai ben connessi fra
loro hanno spesso superato terremoti di sensibile intensità anche se
non erano stati progettati come sismo-resistenti
E’ quindi importante che gli edifici abbiano
• regolarità in pianta e in altezza
• elevata iperstaticità (efficace collegamento fra tutti gli elementi)
• solai rigidi nel proprio piano
Se sono rispettate queste caratteristiche, in condizioni sismiche
l’energia viene dissipata uniformemente in tutti gli elementi della
struttura.
REGOLARITA’ IN PIANTA
Configurazione in pianta compatta e approssimativamente simmetrica
in relazione alla distribuzione di masse e rigidezze.
Rapporto fra i lati del rettangolo in cui l’edificio è inscritto inferiore a 4
Rientri o sporgenze non superiori al 25% della dimensione dell’edificio
I solai possono essere considerati infinitamente rigidi nel loro piano
Area e rigidezza delle murature devono essere approssimativamente
uguali nelle due direzioni
REGOLARITA’ IN PIANTA
Se l’edificio nuovo dovrà avere forme più complesse è necessario
scomporre l’intero edificio in più moduli regolari
REGOLARITA’ IN ALTEZZA
Tutti gli elementi resistenti (pareti) si estendono per tutta l’altezza
Massa e rigidezza rimangono costanti o si riducono gradualmente
con l’altezza (variazioni inferiori al 20%)
Resistenza effettiva/resistenza richiesta calcolata al piano i non
deve differire più del 20% dell’analogo rapporto per un altro piano
Restringimenti della sezione dell’edificio graduali (> 10% a piano e
max 30% fra ultimo e primo piano)
CONFIGURAZIONI IN ALTEZZA
Quindi configurazioni di questo tipo devono essere evitate
ƒ strutture miste con piani o parti di piano realizzate con tipologia
strutturale e materiali diversi
ƒ Strutture con forti rastremazioni ai piani inferiori
EDIFICIO SEMPLICE
Si definisce “edificio semplice” se rispetta, oltre alle caratteristiche
di regolarità in pianta e in altezza, anche le seguenti
ƒ in ognuna delle due direzioni principali siano previste almeno due
pareti di lunghezza, al netto delle aperture, non inferiore al 30% della
larghezza dell’edificio nella medesima direzione
ƒ La distanza tra queste due pareti non sia inferiore al 75% della larghezza dell’edificio nella direzione ortogonale
ƒ Almeno il 75% dei carichi verticali sia portato da pareti che facciano
parte del sistema resistente alle azioni orizzontali
a1
a2
a3
Σ ai > 0.30 L
> 0.75 L
L
EDIFICIO SEMPLICE
Si devono inoltre aggiungere le seguenti condizioni
ƒ Nessun altezza di interpiano sia superiore a 3.5 m
ƒ Il rapporto tra l’area della sezione resistente delle pareti e superficie del
piano terreno non sia inferiore ai valori indicati nella tabella, per
ciascuna delle due direzioni ortogonali
ƒ Il numero di piani non è superiore a 3 per muratura ordinaria e a 4 per
muratura armata.
EDIFICIO SEMPLICE
Se sono rispettate le condizioni per cui un edificio è classificato
“edificio semplice” non è obbligatorio effettuare alcuna analisi e
verifica di sicurezza per le azioni sismiche
E’ quindi sufficiente eseguire le verifiche di capacità portante per i
carichi verticali secondo le indicazioni del D.M. 9.1.1987
In realtà, siccome le azioni orizzontali agenti perpendicolarmente
alla parete incrementano sensibilmente le sollecitazioni, è ragionevole associare alle azioni verticali anche le azioni dovute al vento
spirante perpendicolarmente alla parete in argomento.
In particolare si ritiene necessaria la verifica di cui alla combinazione A del D.M. 9.1.1987 (azione del vento solo perpendicolare al muro)
PARTICOLARI COSTRUTTIVI
• Ad ogni piano deve essere realizzato un cordolo continuo all’intersezione tra solai e pareti
• La larghezza del cordolo deve essere non inferiore allo spessore della
muratura meno 6 cm ed altezza pari a quella del solaio
• L’armatura corrente non sarà inferiore a 8 cm2, le staffe φ 6 ogni 25 cm
• Le travi metalliche o prefabbricate dei solai devono essere prolungate
nel cordolo per almeno la metà della sua larghezza e comunque per
non meno di 12 cm
< 8 cm2
Staffe φ 6
Passo 25 cm
>(t-6 cm)
t
PARTICOLARI COSTRUTTIVI
• Ogni muro resistente alle azioni orizzontali deve essere intersecato da
altri muri ad esso perpendicolari ad interasse non superiore a 7 m
• In corrispondenza degli incroci tra pareti portanti sono prescritte, su
entrambi i lati, zone di parete muraria di lunghezza non inferiore a 1 m,
compreso lo spessore del muro trasversale
• Al di sopra di ogni apertura deve essere realizzato un architrave in c.a.
o in acciaio efficacemente ammorsato alla muratura
Cordolo
>7m
Architrave
<1m
AZIONE SISMICA
L’azione sismica viene ricavata sulla base dello spettro di risposta
elastico dell’accelerazione, la cui forma dipende dal terreno di
fondazione, ma non varia con il livello di sismicità
Lo spettro di risposta elastico dell’accelerazione orizzontale esprime
la massima accelerazione subita da un oscillatore semplice elastico
di periodo proprio T per effetto di un terremoto con accelerazione
orizzontale massima del terreno pari a agS
Un altro parametro che influenza lo spettro elastico è lo smorzamento
viscoso del sistema ξ.
ξ = 2÷3%
per strutture in acciaio
ξ = 3÷7%
per strutture in calcestruzzo armato
ξ = 7÷10%
per strutture in muratura
PARAMETRI DELLO SPETTRO ELASTICO
L’accelerazione di picco è associata alla zona sismica
Zona
Valore di ag
1
0.35g
2
0.25g
3
0.15g
4
0.05g
I parametri S, TB, TC, TD sono definiti per i vari tipi di suolo
Suolo
S
TB
TC
TD
A
1.0
0.15
0.40
2.0
B,C,E
1.25
0.15
0.50
2.0
D
1.35
0.20
0.80
2.0
Lo spettro di risposta elastico dello spostamento si ottiene dalla
 T 
S De (T ) = S e (T ) ⋅ 

 2π 
2
SPETTRO ELASTICO DELLO SPOSTAMENTO
Lo spettro di risposta elastico dello spostamento si ottiene dalla
 T 
S De (T ) = S e (T ) ⋅ 

 2π 
0.14
ag/g=0.25
0.12
Spostamento (m)
2
0.10
0.08
0.06
0.04
0.02
0.00
0
0.5
1
1.5
2
2.5
3
T (sec)
Serve quando si usa l’analisi statica non lineare
SPETTRI DI PROGETTO
SPETTRI DI PROGETTO
0.9
Lo spettro di progetto
per lo SLU si ottiene a
partire dallo spettro
elastico sostituendo al
posto del coefficiente
di smorzamento η il
fattore di struttura q
SPETTRO ELASTICO
0.8
0.7
0.6
0.5
a/g
Lo spettro di progetto
per lo SLD è ottenuto
dividendo lo spettro
elastico per 2.5
SPETTRO DI PROGETTO SLU
0.4
0.3
SPETTRO DI PROGETTO SLD
0.2
0.1
0
0.00
0.50
1.00
1.50
T(s)
2.00
2.50
3.00
COMBINAZIONE DELLE AZIONI
La verifica allo SLU o di danno SLD deve essere effettuata per la
seguente combinazione dell’azione sismica con le altre azioni
Ed = γ I E + Gk + Pk + ∑ (ψ ji Qki )
dove
γI E
Gk
azione sismica per lo stato limite in esame
carichi permanenti al loro valore caratteristico
Pk
valore caratteristico della precompressione, a cadute avvenute
ψji
ψ2i (SLU) coeff. di combinazione per valore quasi-permanente di Qi
ψoi (SLD) coeff. di combinazione per valore raro di Qi
Qki
valore caratteristico dell’azione variabile Qi
MASSE ASSOCIATE ALL’AZIONE SISMICA
Le masse associate ai seguenti carichi gravitazionali devono essere
considerate per la valutazione degli effetti dell’azione sismica
Gk + ∑ (ψ Ei Qki )
ψEi
coefficiente di combinazione di Qi, tiene conto della probabilità
che tutti i carichi ψoiQki (SLD) o ψ2iQki (SLU) siano presenti sulla
intera struttura in occasione del sisma, e si ottiene moltiplicando
ψoi o ψ2i per ϕ
ANALISI DELLA STRUTTURA
La valutazione delle sollecitazioni nella struttura dovute alle azioni
sismiche può essere condotta facendo ricorso ad uno dei seguenti
metodi di analisi
• Analisi statica lineare (o delle forze statiche equivalenti), adeguata
per edifici regolari in altezza. Nel calcolo delle rigidezze degli elementi
deve tener conto sia del contributo flessionale che tagliante. E’ suggerito l’utilizzo di rigidezze fessurate (in alternativa EIfes=0.5 EIint)
• Analisi dinamica modale, si deve considerare un numero di modi tale
da garantire che la somma delle masse modali efficaci sia almeno pari
all’85% della massa totale e che siano inclusi tutti i modi con massa
efficace non inferiore al 5% di MT
• Analisi non lineare (Push-Over), consente di determinare l’intero
diagramma forza-spostamento dell’edificio fino all’incipiente collasso
• Analisi dinamica non lineare, integrazione passo-passo delle
equazioni di moto a partire da un assegnato accelerogramma di
progetto
ANALISI STATICA LINEARE
Si considerano delle forze statiche equivalenti associate alla forma
modale del primo modo di vibrare della struttura
Il primo modo di vibrare può determinarsi con formule empiriche
T1 = 0.09 H
T1 = 0.05 H 0.75
L
oppure utilizzando il metodo di Rayleigh, che ricava il primo modo
dagli spostamenti laterali ai piani si dovuti ad un sistema di forze Fi
n
T1 = 2π
∑W s
i
2
i
1
n
g ∑ Fi si
1
Wi sono i pesi delle masse ad ogni piano
FORZE SISMICHE EQUIVALENTI
Dallo spettro di risposta di progetto, in corrispondenza del periodo
calcolato, si ricava il coefficiente sismico che moltiplicato per la
massa totale esprime la risultante delle forze sismiche equivalenti
Fh = S d (T1 ) W λ g
λ = 0.85 ÷ 1.0
Le forze da applicare a ciascun piano sono date dalla relazione,
basata sulla forma modale del primo modo di vibrare, oppure più
semplicemente ipotizzando una distribuzione triangolare
Fi = Fh
Wi si
∑W j s j
Fi = Fh
Wi zi
∑W j z j
EFFETTI TORSIONALI
In aggiunta all’eccentricità effettiva, si deve considerare un’eccentricità accidentale, spostando il centro di massa di ogni piano, in ogni
direzione considerata, di una distanza pari al 5% della dimensione
massima del piano in direzione perpendicolare all’azione sismica
Diversamente, gli effetti torsionali accidentali possono essere considerati amplificando le forze da applicare a ciascun elemento verticale con il fattore (δ ) risultante dalla seguente espressione
δ = 1+ 0.6 x Le
x
(max 1.3)
è la distanza dell’elemento resistente verticale dal baricentro geometrico dell’edificio, misurata perpendicolarmente alla direzione
dell’azione sismica considerata
Le è la distanza tra i due elementi resistenti più lontani, misurata allo
stesso modo
RISPOSTA NON LINEARE
Nonostante la muratura sia considerato materiale fragile, le prove
sperimentali su campioni e su strutture hanno mostrato che anche
gli edifici in muratura possiedono una significativa capacità di dissipazione di energia che quindi rende possibile la riduzione delle forze
sismiche elastiche.
Per tener conto della risposta non lineare, come per gli altri materiali, si considera un fattore di struttura maggiore dell’unità
La capacità di dissipazione di energia è
espressa dal fattore di duttilità µu=du/de,
non è quindi necessario progettare la
struttura per resistere alla forza He
La struttura va invece progettata per
resistere alla forza Hdu . Il rapporto
q=He/Hdu rappresenta il fattore di struttura
γ = H max H du
q' = γ q
FATTORE DI STRUTTURA E DUTTILITA’
Per le strutture in muratura, che in genere hanno periodi di vibrazione
inferiori a Tm, è più appropriato il criterio di equivalenza energetica.
Ossia due sistemi uno indefinitamente elastico ed uno elastoplastico
raggiungono spostamenti massimi tali da rendere uguali nei due casi
l’energia di deformazione.
du =
µ
d He
2µ − 1
H du =
He
2µ − 1
q = 2µ − 1
FATTORE DI STRUTTURA
La normativa sismica indica per il fattore di struttura per murature
q = 1.5
per muratura ordinaria
q = 2.0
per muratura armata
q = 3.0
per muratura armata se si adotta nella progettazione
la gerarchia delle resistenze
Alcuni risultati sperimentali su modelli
di edificio a tre piani, in muratura ordinaria e armata, provati su tavola vibrante allo ZRMK (Lubiana) hanno mostrato
He
= 2.84
H max
per muratura ordinaria
He
= 3.74
H max
per muratura armata
RIDISTRIBUZIONE DEL TAGLIO
Per evitare di sottostimare eccessivamente la capacità resistente di
una struttura viene permessa, se sono presenti diaframmi rigidi ai
piani, una modifica della distribuzione del taglio alla base delle varie
pareti, ottenuta da un’analisi lineare, fatto salvo l’equilibrio globale
• Riduzione massima del taglio pari al 25% del valore elastico
• Aumento massimo del taglio pari al 33% del valore elastico
Nell’EC8 questi valori di possibile ridistribuzione sono maggiori e
rispettivamente pari al 30% e al 50%.
Soluzione ridistribuita
Analisi elastica lineare
30
40
100
da equil.
30
35
-25%
30
100
da equil.
35
SCHEMATIZZAZIONE DELLA STRUTTURA
Se l’edificio è costituito da pareti continue a tutta altezza collegate
fra loro in corrispondenza dei solai mediante travi snelle o cordoli, si
schematizza la struttura con elementi a mensola
F3
2
F2
1
2
1
3
2
F3
F2
Parete 1
F1
F3
Parete 3
F2
Parete 2
F1
F1
Tipologia strutturale che riguarda generalmente edifici in muratura armata
SCHEMATIZZAZIONE DELLA STRUTTURA
Se l’edificio è costituito da pareti forate, si schematizza la struttura
con elementi a telaio considerando deformabili solo i tratti fra le
aperture e quindi infinitamente rigidi i nodi di intersezione tra aste
F3
3
2
1
2
1
F2
Parete 2
F1
3
F3
F3
F2
F1
F2
Parete 3
F1
Parete 1
I telai piani possono essere anche collegati fra loro mediante tratti infinitamente rigidi
PROCEDIMENTO SEMPLIFICATO
Se la struttura è costituita da pareti forate con fasce di piano molto
più robuste dei maschi (caso molto frequente negli edifici in muratura
non armata) è possibile la schematizzazione a telai tipo shear-type
Inoltre se le pareti non subiscono variazioni dimensionali di rilievo in
altezza si può operare la distribuzione delle forze orizzontali di ogni
piano separatamente
F3
F2
F1
h3
h2
La rigidezza del primo piano della
parete i-esima è la seguente
k
K1i = ∑
j =1
h1
1
h13
h1
+
12 EI1 j χGA1 j
k
= ∑ K1ji
j =1
Nella procedura vista in precedenza, quindi Ki* =K1i (singolo numero),
la matrice di trasferimento Ti è una matrice (1x3), la matrice globale
K** è una matrice (3x3), β contiene i tre spostamenti di piano e F è il
tagliante di piano.
VERIFICHE DI RESISTENZA MASCHI
PRESSOFLESSIONE
TAGLIO
VERIFICHE DI RESISTENZA FASCE DI PIANO
VERIFICHE SLD
Una seconda analisi elastica lineare della struttura va condotta utilizzando i valori dei carichi verticali e delle azioni sismiche relative allo
Stato Limite di Danno per determinare gli spostamenti di piano delle
singole pareti si
Bisogna confrontare che gli spostamenti di interpiano di ogni parete
risultino inferiori ai valori limite imposti dalla normativa
si +1 − si ≤ d r
ANALISI STATICA NON LINEARE
Le forze sismiche che si ricavano dallo spettro di progetto per le
strutture in muratura sono molto elevate in quanto sono stati assunti dei
coefficienti q di struttura cautelativamente bassi, per tener conto della
possibilità di meccanismi di collasso fragili, come la rottura a taglio
dei maschi.
Per tenere conto delle effettive possibilità di resistenza delle strutture in
muratura, e quindi non sottovalutare la loro risposta alle azioni
sismiche, è necessario ricorrere all’analisi statica non lineare.
Le strutture in muratura sono caratterizzate da un’elevata iperstaticità
e quindi se si incrementano gradualmente gli spostamenti di piano si
nota che quando alcune pareti raggiungono il limite elastico le altre
sono ancora ampiamente in campo elastico e quindi si verificano delle
ridistribuzioni di sforzi tra le pareti.
Inoltre le dimensioni delle pareti, soprattutto negli edifici esistenti,
dipendono spesso da ragioni costruttive più che da ragioni statiche, per
cui la sovraresistenza del sistema può essere molto significativa.
DM 1996
EDIFICI NUOVI
S=9
EDIFICI ESISTENTI
ORDINANZA
EDIFICI NUOVI
EDIFICI ESISTENTI
S=9
a/g=0,25
a/g=0,25
CRI=0,07
CRI=0,07
S=1-1,35
S=1-1,35
ε=1-1,3
ε=1-1,3
η=1
η=1
β=β1 β2
β=β1 β2
q=1,5
q=1,5
β1=2
β1=2
β2=1
β2=2
γm=3
γm=1
γm=2
γm=1,4-3
F= S(T) λ/g W
F=CR ε βI W
F=CR ε βI W
F= S(T) λ/g W
CR ε βI=0,14-0,18
CR ε βI=0,28-0,36
S(T)max=0,42-0,56
S(T)max=0,42-0,56
Frd>Fsd =Fsk / γm
Frd>Fsd =Fsk / γm
Frd>Fsd =Fsk / γm
Frd>Fsd =Fsk / γm
γm CR ε βI =0,420,54
γm CR ε βI =0,280,36
γm S(T)max =0,841,12
γm S(T)max =0,591,68
I metodi di analisi non lineare fino ad ora utilizzati si basavano sul
comportamento non lineare dei maschi murari, caratterizzato da un
valore di resistenza ultima a taglio e da uno spostamento ultimo.