CORSO DI LAUREA IN SCIENZE
DELL’ARCHITETTURA
FISICA TECNICA
AMBIENTALE
Trasmissione del calore:
La conduzione – I parte
Prof. Gianfranco Caruso
A.A. 2013/2014
Il Calore
Il Calore è una forma di energia in
transito:: ad esempio un sistema può
transito
scambiare energia con un altro sotto
forma di calore.
calore.
Il passaggio di calore da un sistema
all’altro può avvenire se:
se:
– I due sistemi sono a temperature diverse
– I due sistemi non sono separati da una
superficie adiabatica
adiabatica..
1
Il Calore
Il calore si propaga (spontaneamente
(spontaneamente….
….))
dalle zone a temperatura più alta verso le
zone a temperatura inferiore
Q=0
Parete adiabatica
Q=0
Q≠0
Parete diabatica
Parete diabatica
La Trasmissione del calore
Questa branca della fisica ha un forte carattere sperimentale e
proprio dall’osservazione sperimentale dei fenomeni termici è
possibile mettere in evidenza il fatto che lo scambio termico tra
due corpi, aventi temperatura diversa, può avvenire:
1. per contatto e in assenza di moto relativo tra due corpi;
l’osservazione sperimentale del fenomeno rivela che le
temperature dei due corpi cambiano nel tempo fino a quando
entrambi raggiungono la stessa temperatura, il cui valore risulta
intermedio tra quelli delle loro temperature iniziali;
2. per contatto in presenza di moto relativo tra un corpo ed
un fluido; si osserva che, dopo un certo tempo, il corpo e il
fluido tendono ad assumere la stessa temperatura;
3. senza contatto tra corpi separati anche dallo spazio
vuoto; anche in questo caso l’osservazione sperimentale del
fenomeno evidenzia il fatto che diminuisce la temperatura dei
corpi caldi (raffreddamento) e contemporaneamente aumenta la
temperatura di quelli freddi (riscaldamento).
2
I Meccanismi di
Trasmissione del Calore
La Trasmissione del Calore può dunque avvenire
con meccanismi diversi:
1.
2.
3.
Conduzione
Convezione
Irraggiamento
Conduzione
Raramente i meccanismi
di scambio termico agiscono
singolarmente.
Calore
Irraggiamento
Convezione
La conduzione termica
La conduzione termica si manifesta, macroscopicamente, come uno scambio di energia termica
all’interno di corpi o tra corpi solidi, liquidi o gassosi, in
contatto
tra
di
loro,
senza
movimento
macroscopico di materia.
Lo scambio termico, dal punto di vista microscopico, è
dovuto alla cessione di energia cinetica molecolare
(rotazionale e vibrazionale) da zone ad alta
temperatura verso zone adiacenti a più bassa
temperatura.
3
Il postulato(1) di Fourier
(1768-1830)
A
T1
T2
s
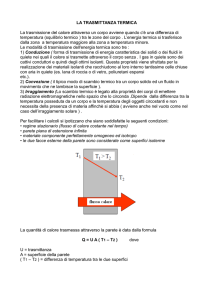
Si consideri una piastra di materiale
omogeneo (struttura del materiale uniforme in
ogni punto) ed isotropo (proprietà termofisiche
indipendenti dalla direzione) di spessore s
perfettamente isolata ai bordi in maniera
tale che il trasferimento del calore avvenga
solo perpendicolarmente alle due superfici
piane e parallele, di area A.
Le
due
superfici
siano
mantenute
costantemente alle temperature uniformi
(superfici isoterme) T1 e T2 (T1 > T2 ;
∆T = T1 - T2 ).
(1) Postulato: affermazione non dimostrata, ma considerata vera
Conduzione
La potenza termica trasmessa per conduzione tra le due superfici è
proporzionale alla differenza di temperatura, all’area A e inversamente
proporzionale allo spessore. Tale proporzionalità è esprimibile tramite
un fattore detto conducibilità termica del materiale λ. Tale
coefficiente, che è una proprietà fisica del materiale e ne misura il
comportamento termico, si misura in W/(m⋅K).
Temperatura della prima
faccia (K, °C)
q = λ ⋅ A⋅
T1 − T2
s
Temperatura della
seconda faccia (K, °C)
Spessore della lastra (m)
Conducibilità termica - W/(m K)
Potenza termica (W)
4
Conduzione
In un sistema cartesiano, ponendo lo spessore della parete lungo
l’asse x, si può scrivere:
q = λ ⋅ A⋅
∆T
∆x
Riducendo a piacere lo spessore ∆x e l’area della superficie, si ha la
seguente espressione in termini differenziali, valida per un
elementino infinitesimo, in cui la potenza termica che attraversa
un’area dA lungo la direzione ad essa perpendicolare x, in cui è
presente un gradiente di temperatura dT/dx, è:
T
dq x = −λ ⋅ dA ⋅
dT
dx
∂T
∂x
Il flusso di calore è
positivo nel verso
delle temperature
decrescenti!
x
Le superfici isoterme
Nel corpo considerato si avranno delle superfici a temperatura
costante (superfici isoterme) che approssimativamente possono
essere individuate, nel caso di una lastra piana, nei piani paralleli alle
due superfici estreme.
Si osserva quindi che il flusso termico si propaga in direzione
perpendicolare alle superfici isoterme ossia, in termini matematici,
lungo la direzione del vettore gradiente di temperatura.
Tale situazione ha una validità
generale, ossia su di un corpo
qualsiasi una volta individuata una
superficie isoterma il flusso di calore
si propagherà in ogni punto in
direzione perpendicolare a tale
superficie.
Le superfici isoterme non si
intersecano mai tra loro in quanto
un punto, in un certo istante, può
avere un solo valore di temperatura.
5
Il campo termico
Il fenomeno della conduzione in un corpo qualunque può essere
descritto solo quando sia noto il campo di temperatura all’interno del
corpo, campo che è in generale funzione delle coordinate spaziali x, y,
z e del tempo τ :
T = f (x,y,z,τ)
Per determinare il campo termico (anche al variare del tempo)
all’interno di un corpo di forma qualunque è necessario risolvere
l’equazione generale della conduzione, ottenibile effettuando un
bilancio di energia (tramite il postulato di Fourier) su un elementino di
dimensioni infinitesime dx⋅dy⋅dz.
Noto il campo di temperatura, sono noti i gradienti di temperatura e
si può calcolare il flusso di calore all’interno del corpo di forma
qualunque. La parete piana infinita in condizioni stazionarie, di cui
abbiamo parlato finora, è un caso semplice.
PARETE PIANA (singolo strato) E
RESISTENZA TERMICA
T1
T2
q
6
CONDUZIONE: PARETE PIANA
E RESISTENZA TERMICA
R=
s
λ
m2 K
W
q ∆T
=
A R
W
2
m
Il flusso termico è inversamente proporzionale alla resistenza
termica R
La Resistenza termica per conduzione a sua volta è:
• Direttamente proporzionale allo spessore della parete;
• Inversamente proporzionale alla conducibilità del materiale della
parete.
A parità di spessore, offriranno una maggiore resistenza termica
al passaggio di calore pareti costituite da materiali con λ più
piccola.
Isolanti termici
λ
R
q/A
Imposta la differenza di temperatura ∆T, al diminuire della
conducibilità termica, aumenta la resistenza termica e quindi
diminuisce la potenza termica (flusso termico) trasmessa per unità
di area.
I materiali isolanti sono caratterizzati da conducibilità termiche molto
basse (inferiori a 0,2 W/mK, valore tipico 0,05 W/mK).
Se il flusso termico fosse imposto, minore è la conducibilità termica,
maggiore sarebbe il salto di temperatura ∆T :
∆T = R ⋅
q
A
[K ]
7
Conducibilità termica
Il valore del coefficiente di conducibilità termica λ
delle diverse sostanze varia entro limiti molto ampi,
dipende dallo stato del materiale e può variare con la
temperatura, la pressione (per i gas) e gli eventuali
trattamenti termici che il materiale ha subito.
La conducibilità termica, come detto, si misura, nel
sistema SI, in W/(m K).
CONDUCIBILITA’ TERMICA
1000
8
CONDUCIBILITA’
TERMICA
La conducibilità
termica,
generalmente,
all’aumentare
della temperatura
aumenta nei gas
e diminuisce nei
solidi
Conduzione: parete piana
q=
T1
T2
λ
s
⋅ A ⋅ ∆T
q ∆T
=
A R
s
R=
s
λ
∆T = R ⋅
[W ]
W
2
m
m2 K
W
q
A
[K ]
POTENZA TERMICA
FLUSSO TERMICO
(AREICO)
RESISTENZA
TERMICA
VARIAZIONE DI
TEMPERATURA
9
Parete “multistrato”
Nel caso, più frequente in edilizia, in cui la lastra piana
sia costituita da più strati affiancati di materiali diversi
(ipotizzando un “contatto termico perfetto”), come si
calcola la potenza termica che attraversa la parete?
Consideriamo una parete costituita da 2 strati di
spessore (sA e sB) e materiale (λA e λB, ad esempio λA
> λB) diversi.
Sono note le due temperature sulle facce esterne della
parete (T1 e T2, ad esempio T1 > T2), mentre NON è,
ovviamente, nota la temperatura dell’interfaccia di
separazione dei due strati (TS)
Parete multistrato
λA
λB
Se fosse nota la temperatura TS
dell’interfaccia potremmo considerare
i due strati separatamente e quindi
scrivere::
scrivere
T1
TS
T2
sA
(T − T )
λ
q
= A ⋅ (T1 − TS ) = 1 S
RA
A A sA
W
2
m
(T − T2 )
λ
q
= B ⋅ (TS − T2 ) = S
RB
A B sB
W
2
m
sB
10
Parete multistrato
λB
λA
q
AA
q
A A
q
A B
T1
TS
q
A B
TS
T2
sA
Poiché non c’è generazione (o sottrazione)
di calore all’interno dei due strati, la potenza
termica “entrante” nello strato (attraverso la
superficie 1, ad esempio per lo strato A) è
uguale alla potenza “uscente” (dalla
superficie S, sempre per lo strato A)
A).. Poiché
anche in corrispondenza dell’interfaccia non
c’è alcuna generazione o sottrazione di
potenza termica, quella che “esce” dallo
strato A sarà pari a quella che “entra” nello
strato B e poi “uscirà” dalla superficie 2. Di
conseguenza si ha certamente
certamente::
q
q
=
A A A B
sB
W
2
m
Parete multistrato
Non essendo nota la temperatura dell’interfaccia TS, non è possibile
calcolare il flusso termico con le relazioni finora note.
Esprimiamo quindi le differenze di temperatura attraverso i due
strati (“cadute” di temperatura).
(T1 − TS ) = q ⋅ R A
A
(TS − T2 ) = q ⋅ RB
Sommando
uguaglianze,
uguaglianza:
i
è
rispettivi
membri
delle
valida anche la seguente
A
(T1 − TS ) + (TS − T2 ) = q ⋅ RA + q ⋅ RB
A
(T1 − T2 ) = q ⋅ (RA + RB )
A
A
q (T1 − T2 )
=
A ( R A + RB )
11
Parete multistrato
Quindi in una parete formata da più strati, ciascuno con la propria
resistenza termica, e soggetta ad una differenza di temperatura
totale (fra le due superfici estreme della parete) ∆T = T1 – T2, il
flusso termico è dato da:
q (T1 − T2 )
=
Rtot
A
W
m 2
In cui Rtot è la resistenza totale della parete, data dalla somma
delle resistenze dei singoli strati che si incontrano passando dalla
temperatura T1 alla temperatura T2. Nel caso di un numero
generico n di strati:
n
Rtot = ∑ R j = R1 + R2 + R3 + ..... + Rn =
j =1
s1
λ1
+
s2
λ2
+
s3
λ3
+ ..... +
sn
λn
m 2 ⋅ K
W
Pareti piane composte e
materiali non omogenei
Nelle applicazioni si incontrano spesso pareti piane composte
da più elementi costruttivi aventi area, spessore e conduttività
diverse tra loro; i casi più comuni sono rappresentati dalle
pareti con fori per finestre, dai solai costituiti da travetti in
calcestruzzo e blocchi in laterizio oppure dalle finestre
costituite dalla parte vetrata e dal telaio.
La denominazione "in parallelo" vuole indicare che questa
configurazione è caratterizzata dal fatto che gli n strati piani
che costituiscono la parete composta sono attraversati da n
flussi termici che seguono percorsi diversi (in parallelo) avendo
tutti origine da un unico sistema o corpo o ambiente alla
temperatura T1 e destinazione unica su un sistema o corpo o
ambiente alla temperatura T2. In sostanza tutti gli strati sono
sottoposti alla stessa differenza di temperatura.
12
Parete costituita da
materiale non omogeneo
∆T
(q/A)A
(q/A)B
(q/A)A
(q/A)B
(q/A)A
s
Nel caso di un materiale non
omogeneo, quale ad esempio un
mattone forato, il flusso di calore non
è uniforme. In linea di principio, ci
saranno flussi di calore diversi a
seconda delle resistenze termiche
incontrate.
Parete costituita da
materiale non omogeneo
In tal caso è bene tener presente che NON SI SOMMANO
I FLUSSI TERMICI PER UNITA’ DI SUPERFICIE
(W/m2), MA SI SOMMANO LE POTENZE TERMICHE
(W)..
(W)
Si calcolano quindi i flussi termici per ciascun
percorso “in parallelo” del calore.
calore. Si moltiplicano poi
i flussi per le relative aree delle superfici
interessate, per ottenere le potenze.
potenze. Infine si
sommano le potenze termiche.
termiche.
Spesso, per questi materiali edilizi disomogenei, viene
fornita la conduttanza equivalente o la resistenza
termica equivalente,
equivalente, e la parete viene trattata
interamente come una parete multistrato con strati
omogenei..
omogenei
13
Conduttanza (C) e
Resistenza (R) equivalenti
RA =
∆T
λ2
λ1
q A = AA ⋅
s2
AB
s
AA
C=
1
R
∆T
= C A AA ∆T
RA
λ1
+
q B = AB ⋅
s2
λ2
+
s1
λ1
∆T
= C B AB ∆T
RB
q
∆T W
= Ceq ⋅ ∆T =
[
]
m2
A
Req
Conduttanza equivalente
A = A A + AB
s1
q = q A + q B = (C A AA + C B AB ) ⋅ ∆T [W ]
Intera
parete
s
RB =
Ceq = C A
AA
A
+ C B B [W 2 ]
m K
A
A
Media pesata sulle aree
Resistenza equivalente
Req =
2
1
[m K ]
W
Ceq
14